Bernoulli numbers serve as coefficients in formulas for sums of powers of natural numbers.
For example:
$$
1 + 2 + \cdots + n = \frac{1}{2}B_0\,n^2 + B_1\,n
$$
And the zeta function relates to Bernoulli numbers by
$$
\zeta(1-s) = -\frac{B_s}{s}.
$$
Here, I explain how the zeta function assigns the value -1/12 to the divergent series of natural numbers.
• Why the zeta function’s natural number series doesn’t diverge (2014/2/8)
In 1644, Italian mathematician Pietro Mengoli posed the problem of evaluating the series:
$$ \frac{1}{1^2} + \frac{1}{2^2} + \frac{1}{3^2} + \cdots. $$Swiss mathematician Jacob Bernoulli attempted to find its value but was unsuccessful. This became known as the Basel problem, named after his hometown of Basel.
In 1735, at age 28, Leonhard Euler solved this problem and showed:
$$ \frac{1}{1^2} + \frac{1}{2^2} + \frac{1}{3^2} + \cdots = \frac{\pi^2}{6}. $$This result was remarkable because it connected a simple infinite series to the geometry of circles. Later, in 1749, Euler discovered an even more astonishing identity:
$$ 1 + 2 + 3 + \cdots = -\frac{1}{12}. $$This equality is quite mysterious—since the series diverges classically, how can it yield a finite value? In 1913, Indian mathematician Srinivasa Ramanujan developed a summation method to explain it.
First, consider the series:
By shifting and adding, one finds:
Next, define the alternating series:
Applying the same shift-and-add technique gives:
Finally, look at the natural-number series:
Multiplying by four and subtracting yields:
Of course, the series 1 + 2 + 3 + ··· diverges, so this method lacks classical rigor. One way to regularize it is to introduce a damping factor, as illustrated below:
Define the damped sum:
$$ H_n(x) = \sum_{k=1}^n k\,e^{-kx}\cos(kx). $$For finite n, as x → 0⁺, Hn(x) approaches 1 + 2 + … + n. However, in the limit n → ∞ and x → 0⁺, this sum converges to −1/12:
$$ \lim_{x\to0^+}\sum_{k=1}^\infty k\,e^{-kx}\cos(kx) = -\frac{1}{12}. $$You can verify this limit numerically on Wolfram|Alpha:
For more details on this technique, see:
This regularization also underlies calculations of the Casimir effect without divergent sums.
In 2015, NS proposed the general regularization formula:
$$ \zeta(1-2t) = \lim_{x\to0^+}\sum_{k=1}^\infty \frac{1}{k^{1-2t}}\,e^{-k^t x}\cos(k^t x). $$For example, setting t=2 confirms ζ(−3)=1/120.
In 1859, Bernhard Riemann defined the zeta function for s by
$$ \zeta(s) = \sum_{n=1}^\infty \frac{1}{n^s}, $$and then extended it analytically to the complex plane via
$$ \zeta(s) = \Gamma(1-s)\oint_{C}\frac{dz}{2\pi i\,z}\,z^s\frac{e^z}{1-e^z}. $$This integral defines the global zeta function, while the original series is often denoted Z(s):
$$ Z(s) = \sum_{n=1}^\infty \frac{1}{n^s}. $$Riemann’s reflection formula relates these definitions:
$$ \zeta(1-s) = \frac{2}{(2\pi)^s}\,\Gamma(s)\,\cos\!\bigl(\tfrac{\pi s}{2}\bigr)\,\zeta(s). $$From this, one can derive ζ(−1)=−1/12. See the graph of the global zeta function:
The image above, rotated and enlarged, resembles a mountainous landscape against a blue sky. Riemann conjectured that all nontrivial zeros have real part ½. This is the Riemann Hypothesis. The first few nontrivial zeros are:
Bernoulli numbers originally arose in formulas for sums of powers of natural numbers. For example, the sums for powers 0-6 are:
| $$1^0 + 2^0 + 3^0 + \cdots + n^0 = \frac{1}{1}n^1$$ |
| $$1^1 + 2^1 + 3^1 + \cdots + n^1 = \frac{1}{2}n^2 + \frac{1}{2}n^1$$ |
| $$1^2 + 2^2 + 3^2 + \cdots + n^2 = \frac{1}{3}n^3 + \frac{1}{2}n^2 + \frac{1}{6}n^1$$ |
| $$1^3 + 2^3 + 3^3 + \cdots + n^3 = \frac{1}{4}n^4 + \frac{1}{2}n^3 + \frac{1}{4}n^2$$ |
| $$1^4 + 2^4 + 3^4 + \cdots + n^4 = \frac{1}{5}n^5 + \frac{1}{2}n^4 + \frac{1}{3}n^3 - \frac{1}{30}n^1$$ |
| $$1^5 + 2^5 + 3^5 + \cdots + n^5 = \frac{1}{6}n^6 + \frac{1}{2}n^5 + \frac{5}{12}n^4 - \frac{1}{12}n^2$$ |
| $$1^6 + 2^6 + 3^6 + \cdots + n^6 = \frac{1}{7}n^7 + \frac{1}{2}n^6 + \frac{1}{2}n^5 - \frac{1}{6}n^3 + \frac{1}{42}n^1$$ |
Jacob Bernoulli published these numbers in 1713. The first few Bernoulli numbers are:
| n | Bₙ |
|---|---|
| 0 | 1 |
| 1 | 1/2 |
| 2 | 1/6 |
| 3 | 0 |
| 4 | -1/30 |
| 5 | 0 |
| 6 | 1/42 |
These numbers appear again in closed-form expressions for sums of powers:
| $$1^0 + 2^0 + 3^0 + \cdots + n^0 = \frac{1}{1}B_0\,n^1$$ |
| $$1^1 + 2^1 + 3^1 + \cdots + n^1 = \frac{1}{2}B_0\,n^2 + B_1\,n$$ |
| $$1^2 + 2^2 + 3^2 + \cdots + n^2 = \frac{1}{3}B_0\,n^3 + B_1\,n^2 + \frac{2!}{1!2!}B_2\,n$$ |
| $$1^3 + 2^3 + 3^3 + \cdots + n^3 = \frac{1}{4}B_0\,n^4 + B_1\,n^3 + \frac{3!}{2!2!}B_2\,n^2$$ |
| $$1^4 + 2^4 + 3^4 + \cdots + n^4 = \frac{1}{5}B_0\,n^5 + B_1\,n^4 + \frac{4!}{3!2!}B_2\,n^3 + \frac{4!}{1!4!}B_4\,n$$ |
| $$1^5 + 2^5 + 3^5 + \cdots + n^5 = \frac{1}{6}B_0\,n^6 + B_1\,n^5 + \frac{5!}{4!2!}B_2\,n^4 + \frac{5!}{2!4!}B_4\,n^2$$ |
| $$1^6 + 2^6 + 3^6 + \cdots + n^6 = \frac{1}{7}B_0\,n^7 + B_1\,n^6 + \frac{6!}{5!2!}B_2\,n^5 + \frac{6!}{3!4!}B_4\,n^3 + B_6\,n$$ |
Bernoulli numbers can be defined via Bernoulli polynomials Bₙ(x). One convention sets Bₙ = Bₙ(1), which we adopt here.
More generally, one can define a Bernoulli function B(s) so that for natural n:
$$ \zeta(-n) = -\frac{B_{n+1}}{n+1}. $$In 1997, S. C. Woon (University of Cambridge) proposed extending this to
$$ \zeta(1-s) = -\frac{B(s)}{s}. $$Viewing B(s) as a continuous function yields the “Bernoulli function.” Its graph appears below:
Substituting B(s) into Riemann’s reflection formula gives:
$$ \zeta(s) = -\frac{(2\pi)^s}{2\,\Gamma(s+1)\cos(\pi s/2)}\,B(s), $$which for even positive integers reduces to:
$$ \zeta(n) = -\frac{(2\pi)^n}{2\,n!}(-1)^{\frac{n}{2}+1}\,B_n. $$From complex analysis, one derives the integral equation:
$$ \zeta(1-s) = \oint_{S^1}\frac{-dt}{2\pi i}\,B(s,t)\,\zeta(t), $$where B(x,y) is Euler’s beta function. For details, see:
Studying its eigenvalues may shed light on the Riemann Hypothesis.
A new proof that 1 + 2 + 3 + ··· = −1/12 based on finite harmonic derivatives is given here:
This approach uses the finite harmonic derivative
$$ H_n^{(s)}(z) = \sum_{k=1}^n \frac{k^s}{k}e^{kz}, $$recovering harmonic numbers, zeta values, and partition functions in limits.
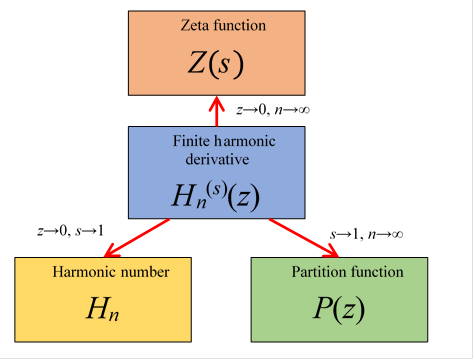
Quantizing this leads to the wave zeta function
$$ Z_q(s) = \sum_{k=1}^\infty \frac{1}{k^s}e^{kq}, $$ $$ \zeta_q(s) = \oint_C\frac{dz}{2\pi i(z-q)}\,Z_z(s), $$whose classical limit q→0 recovers ζ(s):
$$ \lim_{q\to0}\zeta_q(s) = \zeta(s). $$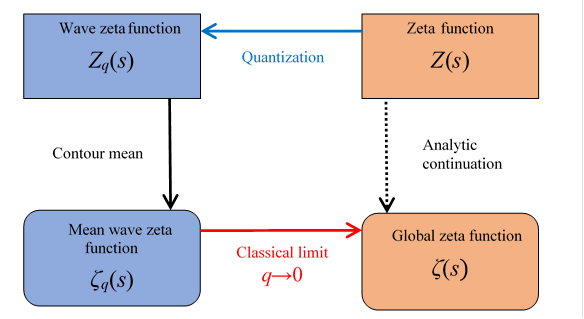
Thus, analytic continuation can be viewed as quantization, contour averaging, and a classical limit.
© 2013, 2015 xseek-qm.net
広告


