Mandelbrot Set of the Zeta Function

[List]

Mandelbrot Set of the Zeta Function

The Classic Mandelbrot Set

The classical Mandelbrot set is the collection of complex numbers c for which z_n does not diverge to infinity in the recurrence

Based on Costas Simeonidis’s GPL‑licensed Mandelbrot viewer, we modified the code and added animation. Although interior points are normally black, we color them here according to their complex value.

Full Mandelbrot View
(Iterations: 64)

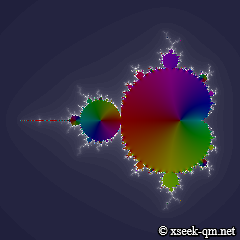
Drag to draw a rectangle and zoom in on that region. The iteration count (recursion depth) defaults to 16. Click [Start] to animate by gradually increasing the iteration count and watch the set form step by step.

Zooming near the origin yields the image below.

Near the Origin
(Iterations: 64)

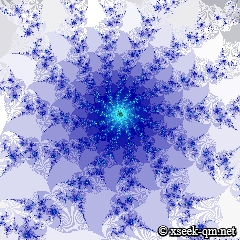
The spiral structure can be viewed here.

Mandelbrot Spiral
(Iterations: 256)

An animation zooms smoothly from the full view down to this spiral.

Exponential‑Map Mandelbrot Set

Replacing the quadratic map with an exponential still yields a Mandelbrot‑like set:

See the result here.

Exponential‑Map Overview
(Iterations: 4)

The default iteration count is 4. Press [Start] to animate as the count increases.

A magnified view around the origin:

Exponential Map near the Origin
(Iterations: 64)

View the spiral region here (rendering may take time):

Exponential‑Map Spiral
(Iterations: 256)

The Zeta Function

The Riemann zeta function is defined by the series

Its graph can be explored here.

Graph of the Zeta Function
(Terms: 16)

Rendering uses HTML Canvas and Web Workers. The term count truncates the series and starts at 16. Click [Start] to animate while increasing the term count and watch zeros appear.

• The color scale increases from black → white → blue → cyan → sky‑blue.
• The dots on the left edge are the trivial zeros.
• The vertical column of black dots marks the non‑trivial zeros.
• The central white spot indicates a pole.

Zeta‑Function Mandelbrot Set

Replacing F(z) with the zeta function also produces a Mandelbrot‑type set:

The complete view is here.

Zeta‑Map Overview
(Iterations: 4, Terms: 16)

Use the [Start] buttons for iterations or terms to animate each parameter separately.

This set was introduced in 1998 by Wuon at Cambridge University (arXiv link).

A zoom near the first non‑trivial zeros (may be slow):

Near the Zeta Zeros
(Iterations: 64, Terms: 8)

See the spiral here (rendering is very slow):

Zeta‑Map Spiral
(Iterations: 256, Terms: 8)

A flower‑like structure emerges.

Comparing the Mandelbrot Variants

Despite differing maps, the various Mandelbrot sets share remarkably similar patterns.

Comparison of Mandelbrot‑Type Sets

F(z)	z2	ez	ζ(z)
Full View
Near Origin/ Zeros
Spiral

Possible reasons for the resemblance:

• The exponential function can be written as a power series.

• The zeta function can be rewritten as a sum of exponentials.

Is There Physical Meaning?

Each point of a Mandelbrot set either converges or diverges to infinity. Likewise, the universe either expands forever or eventually collapses. Perhaps each point corresponds to a distinct universe.

How the Zeta Function Is Computed

Because the naïve series converges slowly, we switch between several formulas as needed:

• Euler-Maclaurin asymptotic expansion
• Knopp-Hasse formula
• Peter Borwein’s acceleration
• The Riemann functional equation when necessary

Accuracy tests for each formula are summarized here:

Accuracy Comparison of the Algorithms

User Guide

Basic Controls

• Drag to draw a rectangle and zoom in.
• The Iteration button changes the recursion depth.
• The Terms button changes the number of series terms.
• [Reset] returns to the initial view.

Animation Controls

• [Start] begins an animation that gradually increases iterations or terms.
• [Stop] halts the animation.

Other Features

• [Zoom out] zooms back.
• [Sizes] changes the canvas size.
• [PNG] saves the current image as a PNG.
• [Animation] auto‑zooms from the current position.

• TZeta Functions and Bernoulli Numbers: Exploring their relationship (2015/4/25)
• Do Imaginary Numbers Exist?: Understanding Them Through Matrices (2015/7/5)
• Actual Infinity vs. Potential Infinity: Two perspectives on infinity (2015/8/3)

広告