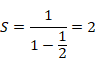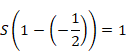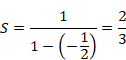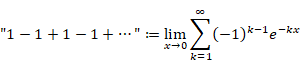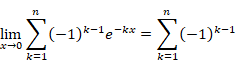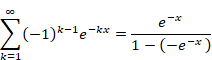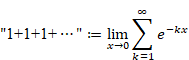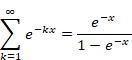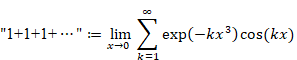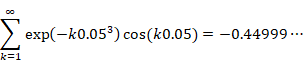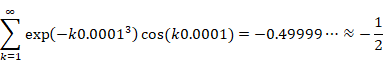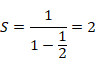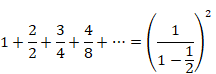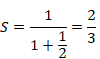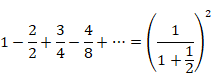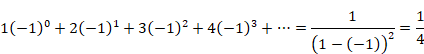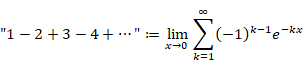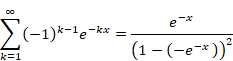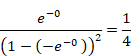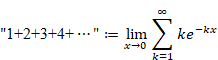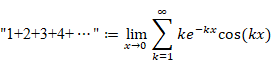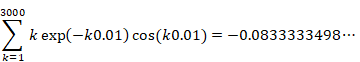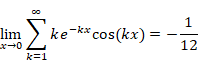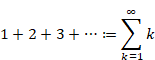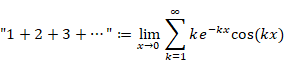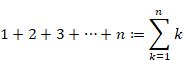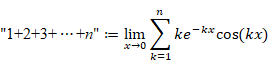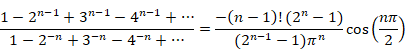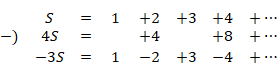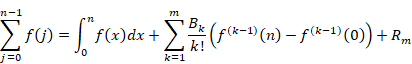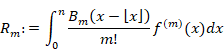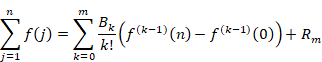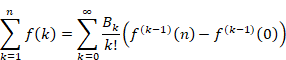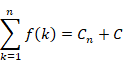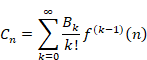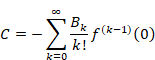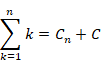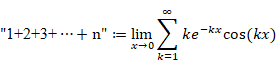Why doesn't the sum of natural numbers of the zeta function diverge to infinity?
Home > Quantum mechanics > Zeta function and Bernoulli numbers
2019/04/07
Published 2014/02/08
K. Sugiyama
The zeta function is the infinite sum of the powers of the reciprocal of natural numbers.
![]()
I will explain why the zeta function ζ (−1) = "1+2+3+4+…" does not diverge to infinity in this article.
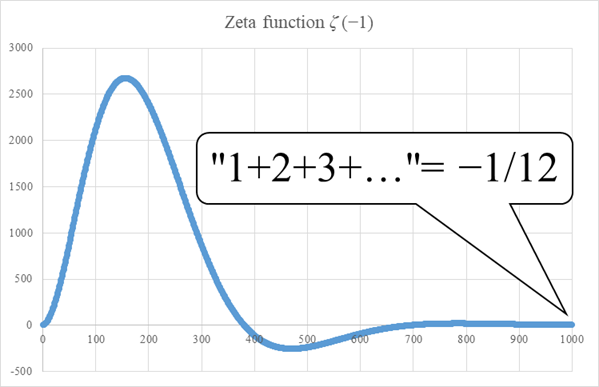
Figure 3-6: Damped oscillation of sum of natural numbers
Euler suggested the following formula in 1749.
"1+2+3+4+…" = −1/12
This is a very mysterious formula. Why doesn’t it diverge to infinity?
Euler, Riemann, and Ramanujan derived this formula. I would like the people to read this article, who want to know the secret of the formula.
The points are as follows.
(1) The normal sum of all natural numbers 1+2+3+4+··· diverges to infinity.
(2) We define the new sum of all natural numbers “1+2+3+4+···+n” which is damped and oscillating very slowly.
(3) It is equal to the normal sum of all natural numbers 1+2+3+4+···+n for the finite terms.
(4) It converges to −1/12 for the infinite terms.
I think that you do not understand the mechanism of damped oscillation only by the explanation mentioned above. In this article, I would like to explain it from the simplest example sequentially to have you understand the mechanism.
Contents
2.2 An alternating geometric series
2.3 An alternating geometric series of the common ratio 1
2.4 A geometric series of the common ratio 1
3 Geometric series of natural numbers
3.1 Geometric series of natural numbers
3.2 Alternating geometric series of natural numbers
3.3 Alternating series of natural numbers
3.4 A series of the natural numbers
6.1 The first opinion: 1+2+3+…=∞
6.2 The second opinion: 1+2+3+…=−1/12
6.3 The third opinion: “1+2+3+…”= −1/12
6.4 The fourth opinion: “1+2+3+…”=−1/12 with damped oscillation
In this article, I will explain the following formula is satisfied.
(Summation formula of natural numbers)
|
|
(1.1) |
One method to understand the complex form is to start with the simplest form and transform it into the complex form little by little. I would like to proceed that method in this article.
The following summation of the geometric progression is called a geometric series.
|
|
(2.1) |
How much will it be?
It will be the area of the graph below.
Figure 2-1: A geometric series
We are not able to estimate the area of this graph.
Therefore, I would like to think it in the following figure.
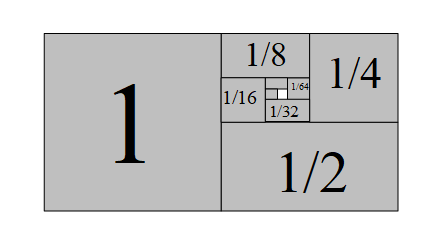
Figure 2-2: A geometric series
It is likely to converge to 2 from this figure. How should we calculate the geometric series?
We calculate it as follows.
|
|
(2.2) |
|
|
(2.3) |
|
|
(2.4) |
We obtain the following formula by subtracting S/2 from S.
|
|
(2.5) |
|
|
(2.6) |
|
|
(2.7) |
|
|
(2.8) |
We obtain the formula of the geometric series of the common ratio r from this result.
(Formula of the geometric series)
|
|
(2.9) |
|
|
(2.10) |
The above formula is satisfied when the limit of the last term is zero.
The geometric series that the signs of the terms alternate between positive and negative is an alternating geometric series, as shown below.
|
|
(2.11) |
It will be the area of the graph below.
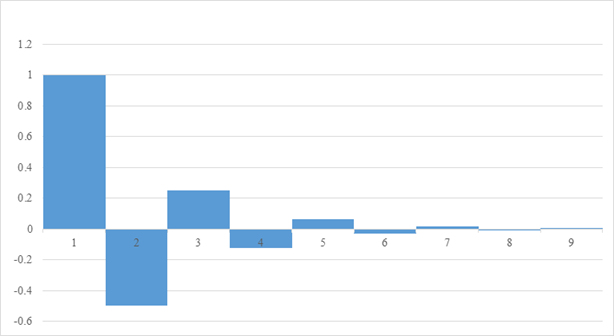
Figure 2-3: An alternating geometric series
We are not able to estimate the area from this graph.
Therefore, I would like to think in the following figure.
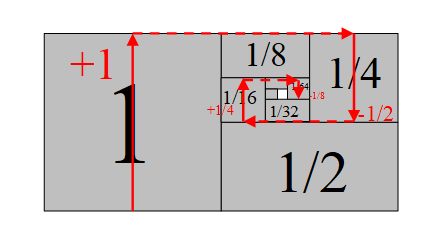
Figure 2-4: An alternating geometric series
In the path of the red arrow, the height from the base is the value of an alternating geometric series. Looking at the figure above, it is likely to converge to 2/3. How should we calculate the alternating geometric series?
We calculate it as follows.
|
|
(2.12) |
|
|
(2.13) |
|
|
(2.14) |
We obtain the following formula by subtracting −S/2 from S.
|
|
(2.15) |
|
|
(2.16) |
|
|
(2.17) |
|
|
(2.18) |
We expand the range of the common ratio r in the formula of the following geometric series from this result.
(The formula of the geometric series)
|
|
(2.19) |
|
|
(2.20) |
I would like to think about the following alternating geometric series of the common ratio 1.
|
|
(2.21) |
This series is sometimes called Grandi's series.
It will be the area of the graph below.
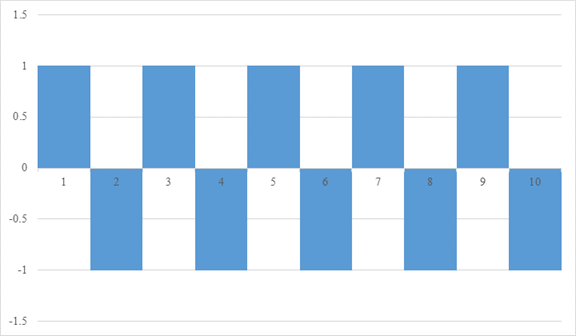
Figure 2-5: Alternating geometric series of the common ratio one
We interpret the formula mentioned above as follows.
|
|
(2.22) |
We obtain the following formula by using the summation of the geometric series.
|
|
(2.23) |
However, −1 is out of a range of the common ratio of the geometric series. In addition, the limit of the last term of the series is not zero. Because the last term is 1 or −1, the answer should be 1 or 0. Why is it 1/2?
Therefore, we will define the following new series.
|
|
(2.24) |
|
|
(2.25) |
The variable x is a very small positive real number. The above series equals the following geometric series when x is zero for the finite term.
|
|
(2.26) |
|
|
(2.27) |
This geometric series is damped very slowly and oscillating.
When I exaggerate the damped alternating and draw it, it becomes the area of the following graph.
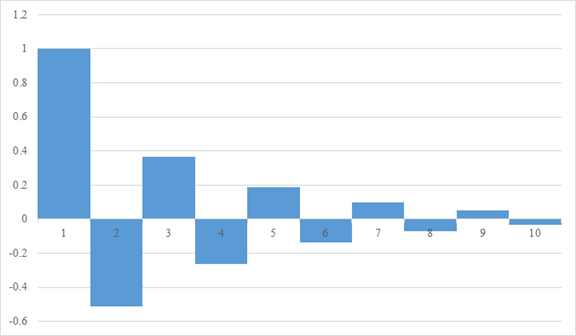
Figure 2-6: A damped alternating geometric series of the common ratio 1
I will write the formula of the geometric series once again.
|
|
(2.28) |
We obtain the value 1/2 by putting zero to the variable x in the result.
|
|
(2.29) |
The last term is zero because it is damped.
We are able to expand the range of the common ratio r in the formula of the following geometric series from this result.
(The formula of the geometric series)
|
|
(2.30) |
|
|
(2.31) |
The alternating geometric series of the common ratio 1 converged cause of the damped oscillation. The damped oscillation can converge the series that does not converge.
I would like to think about the following geometric series of the common ratio 1.
|
|
(2.32) |
It will be the area of the graph below.
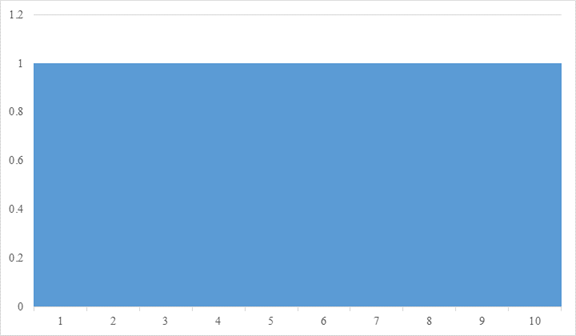
Figure 2-7: A geometric series of the common ratio 1
In order to examine this series, we explain the incorrect calculation method first.
I subtract the next alternating geometric series from the series.
|
|
(2.33) |
Then we obtain the following formula. (This calculation method is incorrect.)
|
|
(2.34) |
We transform it as follows.
|
|
(2.35) |
In other words, it is shown below. (This calculation method is incorrect.)
|
|
(2.36) |
Therefore, the following equation is satisfied.
|
|
(2.37) |
The following equation is satisfied because A is 1/2.
|
|
(2.38) |
However, the limit of the last term of this series is not zero.
Therefore, the above calculation method is incorrect.
Then, we will define the following new series.
|
|
(2.39) |
|
|
(2.40) |
The geometric series is damped very slowly.
I will write the formula of the geometric series.
|
|
(2.41) |
The series diverges by putting zero to the variable x in the result.
|
|
(2.42) |
We are not able to get a good result by using damped series. The geometric series of the common ratio 1 is divergent.
What do we do in order to obtain the good result?
In the previous section, the damped oscillation converged the series that does not converge. Therefore, the damped oscillation might be able to converge the divergent series.
Then, I interpret the geometric series of the common ratio 1 as the following series oscillating slowly with a very long period. Then we may cancel the infinity.
Therefore, I will define the following new series.
(Damped oscillating geometric series of the common ratio 1)
|
|
(2.43) |
|
|
(2.44) |
The variable x is a small number, but the series oscillates very slowly by the effect of the variable.
As the result, we have the following formula.
(Summation formula of natural numbers)
|
|
(2.45) |
You might not believe in the result. Then we calculate it numerically in the next section.
When I exaggerate the damped oscillation and draw it, it becomes the area of the following graph.
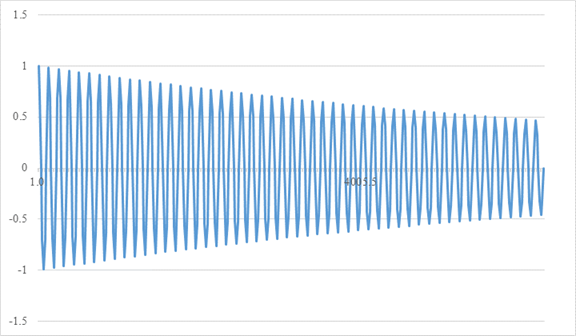
Figure 2-8: Damped oscillating geometric series of the common ratio 1
The calculation formula of the above graph is shown below.
|
|
(2.46) |
We confirm the result by online calculator Wolfram Alpha. Please click the following URL.
https://www.wolframalpha.com/input/?i=
sum_{k=1}^infty exp(-0.05^3 k) cos(0.05 k)
I guess you got the same result.
We also confirm the result in the case of the variable x = 0.0001 by online calculator Wolfram Alpha. Please click the following URL.
http://www.wolframalpha.com/input/?i=
sum_{k=1}^infty exp(-k 0.0001^3) cos(k 0.0001)
The result is shown below.
|
|
(2.47) |
It oscillates at a very long period by the effect of the variable x. In addition, it is damped slowly by the effect of the variable x. As a result, the following equation is satisfied.
|
|
(2.48) |
I would like to think about the following geometric series whose coefficients are natural numbers.
|
|
(3.1) |
In this article, we call it “geometric series of natural numbers” briefly.
It will be the area of the graph below.
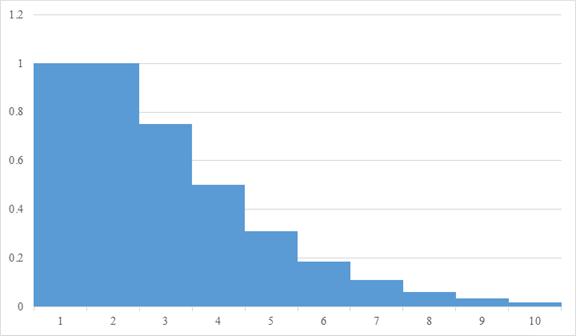
Figure 3-1: Geometric series of natural numbers
How much will it be?
We calculate it as follows.
|
|
(3.2) |
We square the both side.
|
|
(3.3) |
We expand the right side.
|
|
(3.4) |
|
|
(3.5) |
|
|
(3.6) |
Here, I summarize each term of 1, 1/2, 1/4, and 1/8.
|
|
(3.7) |
|
|
(3.8) |
On the other hand, we calculate S as follows.
|
|
(3.9) |
|
|
(3.10) |
Therefore, we are able to calculate S2 as follows.
|
|
(3.11) |
|
|
(3.12) |
We obtain the following formula of the geometric series of the natural numbers from this result.
(The formula of the geometric series of the natural numbers)
|
|
(3.13) |
|
|
(3.14) |
I would like to think about the following alternating geometric series whose coefficients are natural numbers.
|
|
(3.15) |
In this article, we call it “alternating geometric series of natural numbers” briefly.
It will be the area of the graph below.
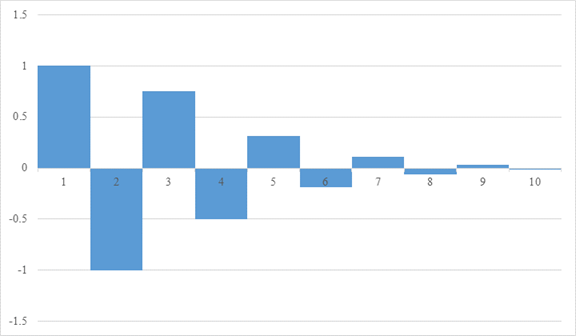
Figure 3-2: alternating geometric series of natural numbers
How much will it be?
We calculate it as follows.
|
|
(3.16) |
We square the both side.
|
|
(3.17) |
We expand the right side.
|
|
(3.18) |
|
|
(3.19) |
|
|
(3.20) |
Here, I summarize each term of 1, 1/2, 1/4, and 1/8.
|
|
(3.21) |
|
|
(3.22) |
On the other hand, we calculate S as follows.
|
|
(3.23) |
|
|
(3.24) |
Therefore, we are able to calculate S2 as follows.
|
|
(3.25) |
|
|
(3.26) |
We are able to expand the range of the common ratio r in the formula of the following geometric series of natural numbers from this result.
(The formula of the geometric series of natural numbers)
|
|
(3.27) |
|
|
(3.28) |
I would like to think about the following alternating series of natural numbers.
|
|
(3.29) |
It will be the area of the graph below.
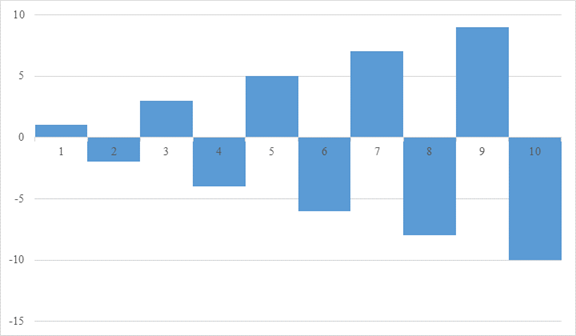
Figure 3-3: Alternating series of natural numbers
We interpret the formula mentioned above as follows.
|
|
(3.30) |
We obtain the following formula by using the summation of geometric series.
|
|
(3.31) |
However, −1 is out of a range of the common ratio of the geometric series of natural numbers. In addition, the limit of the last term of the series is not zero, because the limit of the last term is infinity or minus infinity. Why is it 1/4?
Therefore, I will define the following series.
|
|
(3.32) |
|
|
(3.33) |
The geometric series of the natural numbers increases at first. However, finally it is damped by the effect of the exponential function very slowly.
If we exaggerate the damped alternating, it becomes the area of the next graph.
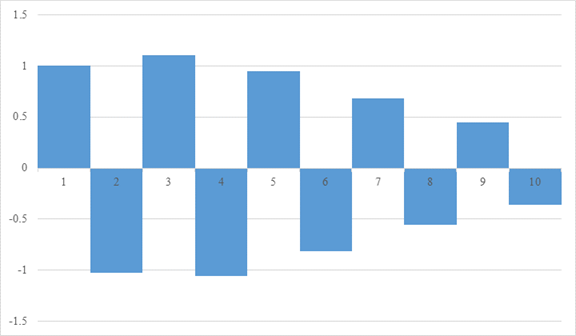
Figure 3-4: Damped alternating series of natural numbers
I will write the formula of the geometric series of the natural numbers once again.
|
|
(3.34) |
If we substitute zero to the variable x of the result, we obtain 1/4.
|
|
(3.35) |
The limit of the last term is zero because it is damped.
We expand the range of the common ratio r in the formula of natural numbers of the following geometric series from this result.
(The formula of the geometric series of natural numbers)
|
|
(3.36) |
|
|
(3.37) |
The alternating series of natural numbers converged cause of the damped oscillation. The damped oscillation can converge the divergent series.
I will think about a series of the following natural numbers.
|
|
(3.38) |
It becomes the area of the following graph.
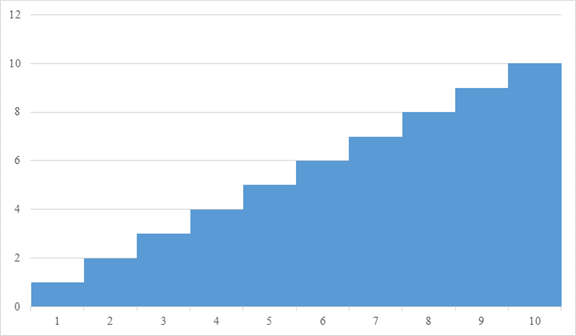
Figure 3-5: A series of natural numbers
In order to examine this series, we explain the incorrect calculation method first.
I subtract the following alternating geometric series of natural numbers from the above series.
|
|
(3.39) |
Then we obtain the following formula. (This calculation method is incorrect.)
|
|
(3.40) |
We transform it as follows.
|
|
(3.41) |
In other words, it is shown below. (This calculation method is incorrect.)
|
|
(3.42) |
Therefore, the following equation is satisfied.
|
|
(3.43) |
The following equation is satisfied because A is 1/4.
|
|
(3.44) |
However, the limit of the last term of this series is not zero. Therefore, the above calculation method is incorrect.
Then, we will define the following new series.
|
|
(3.45) |
|
|
(3.46) |
Though the geometric series of natural numbers increases at first, it is damped very slowly.
I will write the formula of the geometric series.
|
|
(3.47) |
The series diverges by putting zero to the variable x in the result.
|
|
(3.48) |
We are not able to get a good result by using the damped series. The geometric series of natural numbers is divergent.
What do we do in order to obtain the good result?
In the previous section, the damped oscillation converged the divergent series. Therefore, the damped oscillation might be able to converge the geometric series of natural numbers.
Then, I interpret the geometric series of natural numbers as the following series oscillating slowly with a very long period. Then we may cancel the infinity.
Therefore, we will define the following series.
(The damped oscillating geometric series of natural numbers)
|
|
(3.49) |
|
|
(3.50) |
The variable x is a small number, but the series oscillates very slowly by the effect of the variable.
As the result, we have
(Summation formula of natural numbers)
|
|
(3.51) |
You might not believe in the result. Then we calculate it numerically in the next section.
When I exaggerate the damped oscillating, it becomes the area of the following graph.
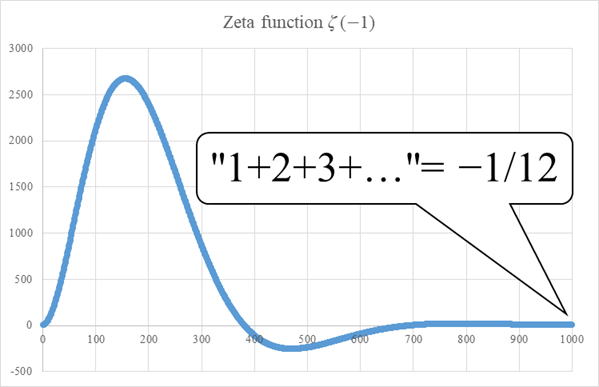
Figure 3-6: Damped oscillation of sum of natural numbers
The calculation formula of the above graph is shown below.
|
|
(3.52) |
This value is very close to the following −1/12.
|
|
(3.53) |
We confirm the result by online calculator Wolfram Alpha. Please click the following URL.
https://www.wolframalpha.com/input/?i=
sum k exp(-k 0.01) cos(k 0.01), k=1 to 3000
I guess you got the same result.
I thought that I wanted to observe how the natural number is continuously changing to −1/12. In the Figure 3-6 above, I can actually observe how the natural number sum changes to −1/12.
We also confirm the result in the case of the limit of the variable x = 0 by online calculator Wolfram Alpha. Please click the following URL.
http://www.wolframalpha.com/input/?i=
lim_{x→0+}sum_{k=1}^infty
k exp(-kx)cos(kx)
I guess you got the following result.
|
|
(3.54) |
It oscillates at a very long period by the effect of the variable x. In addition, it is damped slowly by the effect of the variable x. As a result, the following equation is satisfied.
(The summation formula of natural numbers)
|
|
(3.55) |
We explain the mechanism in the following paper.
- New proof that the sum of natural numbers is −1/12 of the zeta function
https://xseek-qm.net/Regularization_e.htm
I think that some person has the following opinion for this result.
The following two expressions are different. Therefore, it is natural to give different calculation results.
|
|
(3.56) |
|
|
(3.57) |
|
|
(3.58) |
They are surely different expressions. However, the variable x is a very small number. Therefore, in the case of the finite number of terms, the above two expressions are equivalent.
|
|
(3.59) |
|
|
(3.60) |
|
|
(3.61) |
However, they are different for the infinite terms as follows.
|
|
(3.62) |
|
|
(3.63) |
The following series diverges.
|
|
(4.1) |
Here, we define the following series.
|
|
(4.2) |
|
|
(4.3) |
They are equivalent for the finite term as follows.
|
|
(4.4) |
However, they are different for the infinite terms as follows.
|
|
(4.5) |
|
|
(4.6) |
In supplement, I will summarize the information that will be helpful.
Leonhard Euler [1] discovered the following functional equation in 1749 and published it in 1768.
We can obtain the following formula from the above equations.
(Summation formula of natural numbers)
|
|
(5.3) |
Actually, Euler did not write the above formula clearly. Therefore, it is unclear whether Euler summed the series to −1/12 in fact.
Riemann [2] defined the following zeta function in 1859.
(The definitional series of the Riemann zeta function)
|
|
(5.4) |
In addition, he showed the following functional equation.
|
|
(5.5) |
We are able to continue the domain of the argument of the zeta function by suing the functional equation.
It is an analytic continuation to continue the domain of the argument of the function in such way.
We can obtain the following formula from the above equation.
(Summation formula of natural numbers)
|
|
(5.6) |
Ramanujan[3] showed the following formula in 1913.
(Summation formula of natural numbers)
|
|
(5.7) |
Ramanujan’s calculation method of the divergent series is shown below, though the calculation method is not correct since the limit of the last term of this series is not zero.
We express the following value by S
|
|
(5.8) |
We multiply the above formula by four.
|
|
(5.9) |
|
|
(5.10) |
We subtract 4S from S as follows. (This calculation method is not correct.)
|
|
(5.11) |
On the other hand, the following equation is satisfied.
|
|
(5.12) |
Therefore, the following equation is satisfied.
(Summation formula of natural numbers)
|
|
(5.13) |
I think that Ramanujan used the above incorrect calculation method because he had obtained the same result in his own method.
He used Euler–Maclaurin summation formula in order to obtain the result.
(Euler–Maclaurin summation formula)
|
|
(5.14) |
The error term (remainder term) Rm of the above formula is shown below.
|
|
(5.15) |
The above polynomials Bm(x) is Bernoulli polynomials.
We change the definition of Bernoulli number B1 from −1/2 to 1/2 in order to express the Euler–Maclaurin formula briefly.
|
|
(5.16) |
In addition, we define the integral by the following symbol.
|
|
(5.17) |
Then, we are able to express the Euler–Maclaurin formula briefly as follows.
(Euler–Maclaurin summation formula)
|
|
(5.18) |
In addition, we assume the function f (k) is such that the error term Rm tends to zero as the natural number n tends to infinity.
Then, we are able to express the Euler–Maclaurin summation formula as follows in the condition that the natural number n tends to infinity.
(Euler–Maclaurin summation formula)
|
|
(5.19) |
Ramanujan separated the above formula into a term Cn dependent on the natural number n and another constant term C independent of the natural number n.
|
|
(5.20) |
|
|
(5.21) |
|
|
(5.22) |
We call the method for assigning the above constant term C to the value of divergent series Ramanujan summation.
Here, we think the case that the function f (k) is a natural number k.
|
|
(5.23) |
Then, we are able to express the sum of natural numbers as follows.
|
|
(5.24) |
|
|
(5.25) |
|
|
(5.26) |
Therefore, the sum of natural numbers is −1/12 by using Ramanujan summation.
However, I do not understand the reason to ignore the term Cn dependent on the natural number n well.
There seem to be the following opinions about the zeta function ζ (−1) = “1+2+3+…”
This article proposed the fourth opinion.
Some person proposes the following about the zeta function of the series of natural numbers.
At a point of view of the analytic continuation, the left side of the following expression equals to −1/12.
|
|
(6.1) |
On the other hand, the left side of the following expression does not equal to right side.
|
|
(6.2) |
The left side of the expression diverges to infinity.
|
|
(6.3) |
However, I wanted to understand a series of the natural number of the zeta function somehow, and I wrote this article.
Some person proposes the following about the zeta function of the series of natural numbers.
At a point of view of the analytic continuation, the left side of the following expression equals two −1/12.
|
|
(6.4) |
On the other hand, we are able to express the zeta function as follows.
|
|
(6.5) |
Therefore, the left side of the expression equals to -1/12.
|
|
(6.6) |
However, how do we obtain the result?
Some person proposes the following about the zeta function of the series of natural numbers.
At a point of view of the analytic continuation, the left side of the following expression equals to -1/12.
|
|
(6.7) |
On the other hand, we are able to “interpret” that the left side of the following expression equals to the right side.
|
|
(6.8) |
Therefore, we are able to “interpret” that the left side of the expression equals to −1/12.
|
|
(6.9) |
However, what does the "interpretation" mean?
This article proposes the following about the zeta function of the series of natural numbers.
Left side of the following expression diverges to infinity.
|
|
(6.10) |
We define the following sum of special natural numbers with double quotes.
|
|
(6.11) |
|
|
(6.12) |
The finite sum of special natural numbers is equal to the sum of normal natural numbers.
|
|
(6.13) |
On the other hand, infinite sum of special natural numbers is equal to −1/12.
|
|
(6.14) |
We are able to observe how the special sum approaches gradually from normal sum of natural numbers to -1/12. by using the this definition.