The next article discusses the matrix representation of imaginary numbers.
• Why is the square of the imaginary unit i equal to −1? [2014/6/29]When I first encountered imaginary numbers, I was completely confused.
$$ i^2 = -1 $$No real number squared equals −1, so the very idea of assuming such a number felt deeply unsettling. I suspected that introducing a bizarre entity like this would eventually lead to a contradiction. Yet no matter how far I calculated, no inconsistencies appeared. On the contrary, the theory snapped together like a puzzle whose missing piece had finally been found. That led me to a different question.
“If this number isn’t supposed to exist, why does it work so well?”
Still wrestling with that question, I came across a math problem that defined the following matrix:
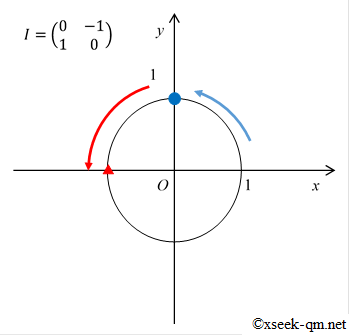
$$ I = \left(\begin{array}{cc} 0 & -1 \\ 1 & 0 \\ \end{array}\right) $$This matrix I is called the matrix representation of the imaginary unit, and its algebra is identical to that of i. For example,
$$ I^2 = -E $$I interpreted this discovery as follows:
“The symbol i is simply shorthand for the matrix I.”
Suppose you meet the quadratic equation
$$ x^2 - 2x + 2 = 0 $$and reinterpret it as a matrix equation
$$ X^2 - 2X + 2E = 0 . $$The solutions then arise naturally as
$$ X = E \pm I , $$which we read back as the familiar
$$ x = 1 \pm i . $$Seen this way, my doubts vanished—I finally understood.
In my view, complex numbers are clearer when introduced through matrices rather than quadratics. From the quadratic perspective, an imaginary number seems like a “non‑existent” entity. From the matrix perspective, however, getting a negative identity after squaring is perfectly natural.
To make that idea accessible, I wrote a companion article that starts with matrices. There I call the matrix I the imaginary‑unit matrix or, more suggestively, the rotation‑unit matrix.
My goal is to reduce the number of people who struggle with imaginary numbers the way I did. Because the article assumes some familiarity with matrices, its intended readers are those who have already studied them.
When I first learned matrices, their manipulation rules struck me as odd. I practiced blindly until I discovered that matrices describe linear transformations. Explaining a matrix as “shorthand for a linear transformation” makes those rules feel perfectly natural.
Because a matrix itself cannot be sketched, developing geometric intuition is hard. To help, I visualized how the unit circle is transformed by various matrices:
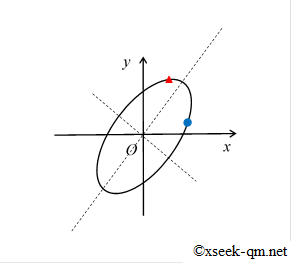
The blue dot shows where the point (1, 0) lands; the red triangle shows the image of (0, 1). At first glance the ellipse’s principal axes look like eigenvectors, but in general they are not:
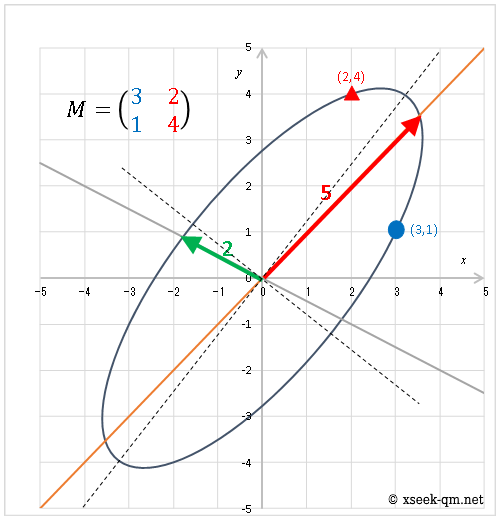
The article ends with the singular value decomposition (SVD), which further clarifies matrices. SVD splits any matrix into right rotation, horizontal scaling, vertical scaling, and left rotation:
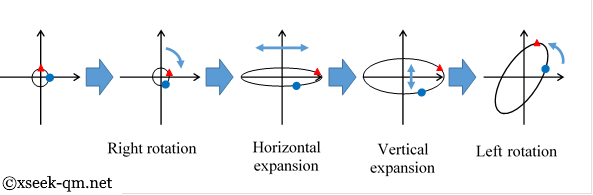
Treating every matrix as an ellipse makes these invisible objects visible, a powerful benefit.
One can deny the existence of a number by proof by contradiction:
“If assuming a number exists leads to a contradiction, that number does not exist.”
The contrapositive is
“If a number exists, assuming its existence will not cause a contradiction.”
Because assuming imaginary numbers causes no contradictions, it is tempting to say they exist. Yet that inference goes from conclusion to premise—logically invalid. The absence of contradiction does not guarantee existence.
Intuitively, a square equalling −1 feels impossible, and the discomfort lingers. Why is it so contrary to our intuition?
A way to ease the discomfort is to regard an imaginary number as shorthand for a rotation‑unit matrix:

Rotation matrices are everyday tools—we never doubt that rotations exist. If an imaginary number is merely a symbol for such a rotation, perhaps its existence is easier to accept.
The word imaginary suggests something unreal, but as we have seen, imaginary numbers correspond to concrete rotation transformations. To avoid the misconception that they “don’t really exist,” I propose a new name.
Calling them numbers at all may be the root of confusion. In everyday language, number means a count of objects—a natural number. Mathematics has repeatedly stretched the term, but each stretch thins its meaning.
Integers can represent positions, real numbers can represent lengths, and so on, but imaginary numbers are different. They should no longer be called numbers; they are units of rotational transformation. I therefore propose the terms rotation‑transformation unit or simply rotation unit.
Textbooks typically say:
“Call any number whose square is −1 the imaginary unit.”
Most people reply, “But such a number doesn’t exist!” Instead, why not teach it this way?
“Call any transformation that rotates an image by 180 degrees after two applications a rotation unit.”
No one doubts such transformations exist—in fact there are two of them, +i and −i. Prompting students to notice that distinction deepens learning.
I believe in the power of good names. Even if a name is less than perfectly formal, clarity can win more hearts to mathematics.
© 2014, 2015 xseek-qm.net
広告


