ベルヌーイ数とは、自然数のべき乗和の公式の係数です。
たとえば、自然数和の公式は2個のベルヌーイ数で表現できます。
$$
1 + 2 + 3 + \cdots + n=\frac{1}{2}B_0 n^2 + B_1 n^1
$$
ゼータ関数は、このベルヌーイ数で表現できます。
$$
\zeta(1-s) = - \frac{B_s}{s}
$$
本ページでは、ゼータ関数の自然数和が-1/12に収束する仕組みを説明します。
•なぜゼータ関数の自然数の和は無限大に発散しないのか? [2014/2/8]
イタリアの数学者ピエトロ・メンゴリは、 1644年に次の級数に関する問題を提出しました。
$$ \frac{1}{1^2} + \frac{1}{2^2} + \frac{1}{3^2} + \cdots $$スイスの数学者ヤコブ・ベルヌーイは、この値を求めようとしましたが、 求めることはできませんでした。 彼の出身地がスイスのバーゼルだったため、 この問題はバーゼル問題と呼ばれています。 1735年に28歳だったオイラーがこの難問を解き、 一躍有名となりました。 その値は次のとおりです。
$$ \frac{1}{1^2} + \frac{1}{2^2} + \frac{1}{3^2} + \cdots = \frac{\pi^2}{6} $$値が円周率を含むため、 これは驚くべき結果です。 1749年に彼は、さらに驚くべき結果を得ました。
この式はとても不思議です。 なぜ無限大に発散しないのでしょうか? インドの数学者ラマヌジャンは1913年に次のように計算しました。
最初に次の値を求めます。
ひとつずらして足してみましょう。
|
そして次の値を求めます。
ひとつずらして足してみましょう。
|
最後に次の値を求めます。
上記の式を4倍します。
次のように、Sから4Sを引きます。
|
上記の計算方法は、自然数の総和が収束するならば正しいです。 しかし、収束しなければ正しくありません。 どうすれば収束させることができるでしょうか? 私は、自然数の総和は次のグラフのように非常にゆっくりと 減衰振動すると考えています。
減衰振動する次の関数を定義します。
$$ H_n(x)=\sum_{k=1}^n k \exp(-kx)\cos(kx) $$この関数は有限の n に対し x = 0 の極限で自然数和に一致します。
$$ \lim_{x \to 0 + }\sum_{k=1}^n k \exp(-kx)\cos(kx) = 1 + 2 + 3 + \cdots + n $$しかし、無限の n に対し-1/12に収束します。
$$ \lim_{x \to 0 + } \sum_{k=1}^\infty k \exp(-kx)\cos(kx)=-\frac{1}{12} $$この驚くべき結果はオンライン計算機 WolframAlpha で確認できます。 次のURLをクリックすると計算できます。
その仕組みは、次の記事で説明したいと思います。
数学に慣れている方には次の論文で説明したいと思います。
その論文の結果を利用することで、カシミール効果を発散なく計算できます。
2015年3月27日には、NSさんが次の公式を発見し、発表されました。
$$ \zeta(1-2t)=\lim_{x \to 0 + } \sum_{k=1}^\infty \frac{1}{k^{1-2t}} \exp(-k^tx)\cos(k^tx) $$ たとえば、ζ(-3)=1/120 は次のとおりです。リーマンは1859年に次のゼータ関数を定義しました。
$$ \zeta(s)=\frac{1}{1^s} + \frac{1}{2^s} + \frac{1}{3^s} + \cdots $$リーマンはさらに、上記のゼータ関数の解析接続を定義しました。
$$ \zeta(s)=\Gamma(1-s)\oint_{C} \frac{dz}{2\pi iz} z^s \frac{e^z}{1-e^z} $$上記の関数を大域ゼータ関数と呼びます。 一般に、通常のゼータ関数と大域ゼータ関数は等しくありません。 そこで、二つの関数を区別するための通常のゼータ関数を文字Zで表記します。
$$ Z(s)=\frac{1}{1^s} + \frac{1}{2^s} + \frac{1}{3^s} + \cdots $$彼は、大域ゼータ関数に対し次の反射公式を得ました。
$$ \zeta(1-s) = \frac{2}{(2\pi)^s}\;\;\Gamma(s)\;\;\cos \Bigl(\frac{\pi}{2}s \Bigr) \; \zeta(s) $$この反射公式で、不思議な公式の−1/12を導くことができます。 大域ゼータ関数のグラフを次のページで確認できます。
本ページの冒頭の画像は、上記の図を 右に90度回転させ描画範囲を拡大したものです。 青い空を背景とした山のように見えます。
彼は次のことを予想しました。
これは「リーマン予想」と呼ばれています。 非自明な零点 ρm の一部は次のとおりです。
みなさんは、自然数のべき乗和を計算したことはありますか? たとえば、n個の自然数の 0, 1, 2, ..., 6 乗和は次のようになります。
| $$ 1^0 + 2^0 + 3^0 + \cdots + n^0 = \frac{1}{1} n^1 $$ |
| $$ 1^1 + 2^1 + 3^1 + \cdots + n^1 = \frac{1}{2} n^2 + \frac{1}{2} n^1 $$ |
| $$ 1^2 + 2^2 + 3^2 + \cdots + n^2 = \frac{1}{3} n^3 + \frac{1}{2} n^2 + \frac{1}{6} n^1 $$ |
| $$ 1^3 + 2^3 + 3^3 + \cdots + n^3 = \frac{1}{4} n^4 + \frac{1}{2} n^3 + \frac{1}{4} n^2 $$ |
| $$ 1^4 + 2^4 + 3^4 + \cdots + n^4 = \frac{1}{5} n^5 + \frac{1}{2} n^4 + \frac{1}{3} n^3-\frac{1}{30} n^1 $$ |
| $$ 1^5 + 2^5 + 3^5 + \cdots + n^5 = \frac{1}{6} n^6 + \frac{1}{2} n^5 + \frac{5}{12} n^4-\frac{1}{12} n^2 $$ |
| $$ 1^6 + 2^6 + 3^6 + \cdots + n^6 = \frac{1}{7} n^7 + \frac{1}{2} n^6 + \frac{1}{2} n^5-\frac{1}{6} n^3 + \frac{1}{42} n^1 $$ |
ヤコブ・ベルヌーイは1713年に ベルヌーイ数を発表しました。それは次のような数字です。
| n | Bn |
|---|---|
| 0 | 1 |
| 1 | 1/2 |
| 2 | 1/6 |
| 3 | 0 |
| 4 | -1/30 |
| 5 | 0 |
| 6 | 1/42 |
n個の自然数の 0, 1, 2, ..., 6 乗和は ベルヌーイ数で次のように表現できます。
| $$ 1^0 + 2^0 + 3^0 + \cdots + n^0=\frac{1}{1}B_0 n^1 $$ |
| $$ 1^1 + 2^1 + 3^1 + \cdots + n^1=\frac{1}{2}B_0 n^2 + B_1 n^1 $$ |
| $$ 1^2 + 2^2 + 3^2 + \cdots + n^2=\frac{1}{3}B_0 n^3 + B_1 n^2 + \frac{2!}{1!2!}B_2 n^1 $$ |
| $$ 1^3 + 2^3 + 3^3 + \cdots + n^3=\frac{1}{4}B_0 n^4 + B_1 n^3 + \frac{3!}{2!2!}B_2 n^2 $$ |
| $$ 1^4 + 2^4 + 3^4 + \cdots + n^4=\frac{1}{5}B_0 n^5 + B_1 n^4 + \frac{4!}{3!2!}B_2 n^3 + \frac{4!}{1!4!}B_4 n^1 $$ |
| $$ 1^5 + 2^5 + 3^5 + \cdots + n^5=\frac{1}{6}B_0 n^6 + B_1 n^5 + \frac{5!}{4!2!}B_2 n^4 + \frac{5!}{2!4!}B_4 n^2 $$ |
| $$ 1^6 + 2^6 + 3^6 + \cdots + n^6=\frac{1}{7}B_0 n^7 + B_1 n^6 + \frac{6!}{5!2!}B_2 n^5 + \frac{6!}{3!4!}B_4 n^3 + B_6 n^1 $$ |
ベルヌーイ数の定義には2種類あります。 ベルヌーイ多項式を Bn (x ) としたとき、 次の2種類です。
本ページでは、 後に説明するベルヌーイ関数の定義と合わせるため、 後者の定義を採用します。
一般に自然数 n について次の式が成立します。
$$ \zeta(-n) = - \frac{B_{n + 1}}{n + 1} $$ケンブリッジ大学のウーンは1997年に、 複素数 s に対し、次の等式を提示しました。
$$ \zeta(1-s) = - \frac{B(s)}{s} $$彼は、ベルヌーイ数 Bn を ベルヌーイ関数 B (s) と解釈しました。 上記の式を「ベルヌーイ関数の等式」と呼ぶこととします。 そのグラフは次のページで見ることができます。
本ページでは、ベルヌーイ数の従来の表記にもとづき、 ベルヌーイ関数 B (s) をBsと表現します。
リーマンの反射公式に「ベルヌーイ関数の等式」を適用すると 次の式が成立します。
$$ \zeta(s) = -\;\;\frac{(2\pi)^s}{2}\;\;\frac{1}{\Gamma(s + 1)} \;\; \frac{1}{\cos(\pi s/2)}\;\;B_s $$2以上の偶数sに対し次の式が成立します。
$$ \zeta(s) = -\;\; \frac{(2\pi)^s}{2}\;\; \frac{1}{s!} \;\;(-1)^{\frac{s}{2} + 1}\;\; B_s $$上記の式は、2以上の偶数nに対する次の公式と等しくなります。
$$ \zeta(n) = -\;\;\frac{(2\pi)^n}{2}\;\; \frac{1}{n!}\;\;(-1)^{\frac{n}{2} + 1}\;\; B_n $$上記の事実はベルヌーイ関数の等式が妥当であることを示唆します。
複素解析で、次の反射積分方程式を導出できます。
$$ \zeta(1-s)=\oint_{S^1} \frac{-dt}{2\pi i} B(s,t) \zeta(t) $$上記の式では、オイラーのベータ関数 B (x, y) を使いました。 導出方法は次の論文で説明しています。
四元数解析で、次の反射積分方程式を導出できます。
$$ \zeta(1-s)=\oint_{S^1} \frac{-dt}{2\pi u} B(s,t) \zeta(t) $$uは単位四元数です。 導出方法は次の論文で説明しています。
反射積分方程式の固有値を調べることで リーマン予想に迫ることができるかもしれません。 また、超弦理論がベータ関数から始まったことも申し添えておきたいと思います。
次の論文で新しい証明方法を説明しています。
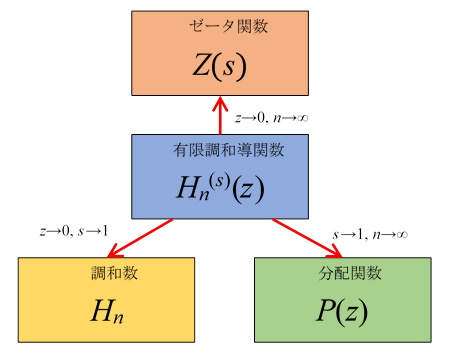
この論文は、有限調和導関数を導入しました。
$$ H^{(s)}_n(z) = \sum_{k=1}^n \frac{k^s}{k} \exp(kz) $$有限調和導関数の極限が調和数になります。
$$ H_n = \sum_{k=1}^n \frac{1}{k} = \lim_{s \to 0} \lim_{z \to 0}H^{(s)}_n(z) $$有限調和導関数の極限がゼータ関数になります。
$$ Z(s) = \sum_{k=1}^n \frac{1}{k^s} = \lim_{z \to 0} \lim_{n \to \infty}H^{(1-s)}_n(z) $$有限調和導関数の極限が分配関数になります。
$$ P(z) = \sum_{k=1}^\infty e^{kz} = \lim_{s \to 1} \lim_{n \to \infty}H^{(s)}_n(z) $$それらの関数の関係は次の図のとおりです。
そして、ゼータ関数Z(s)を量子化し、 波動ゼータ関数Zq(s)を定義します。
$$ Z(s) = \sum_{k=1}^\infty \frac{1}{k^s} $$ $$ Z_q(s) = \sum_{k=1}^\infty \frac{1}{k^s} \exp(kq) $$この波動ゼータ関数の周回平均を取り、平均波動ゼータ関数を定義します。
$$ \zeta_q(s)=\oint_{C} \frac{dz}{2\pi i(z-q)}Z_z(s) $$上記の平均波動ゼータ関数の古典極限が、大域ゼータ関数と一致します。
$$ \lim_{q\to0}\zeta_q(s)=\zeta(s) $$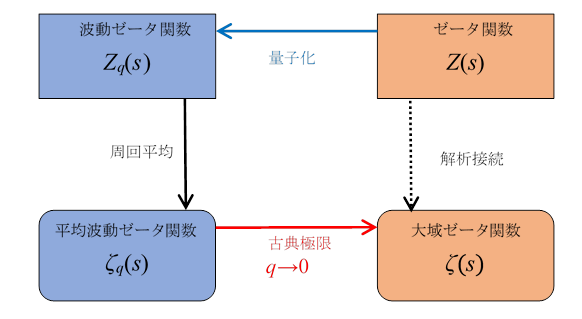
上記のように解析接続は、関数を量子化し、 その関数の周回平均値を計算し古典極限を取る操作と解釈できます。
© 2013, 2014 xseek-qm.net
広告


