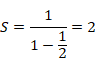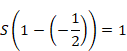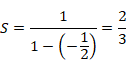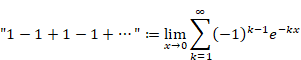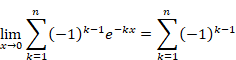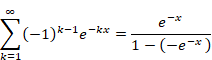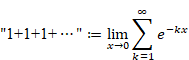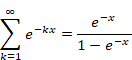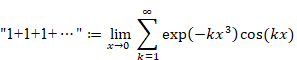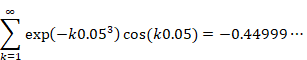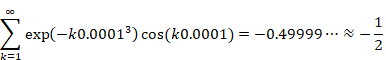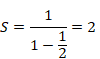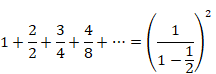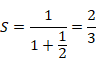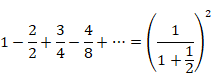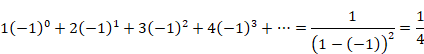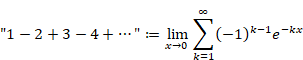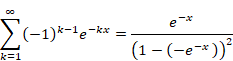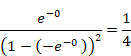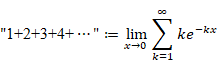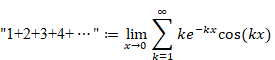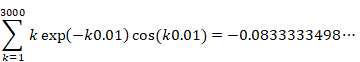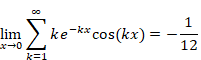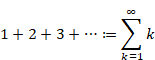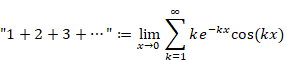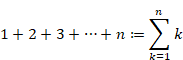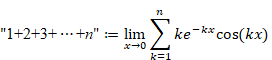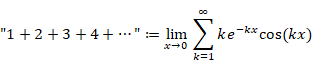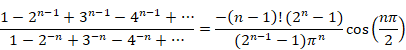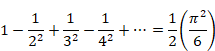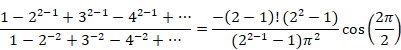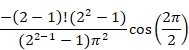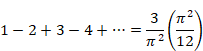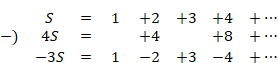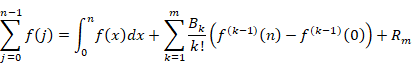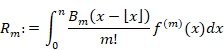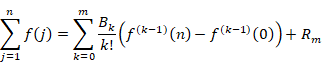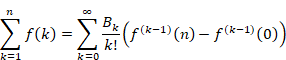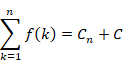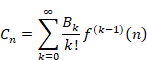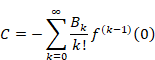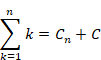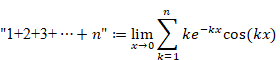なぜゼータ関数の自然数の和は無限大に発散しないのか?
ホーム > 量子力学 > ゼータ関数とベルヌーイ数
2019/05/16
公開日 2014/02/08
K. Sugiyama
ゼータ関数とは、自然数の逆数のべき乗の無限和です。
![]()
本記事は、ゼータ関数 ζ (−1) = "1+2+3+4+…" が無限大に発散しない理由を説明します。
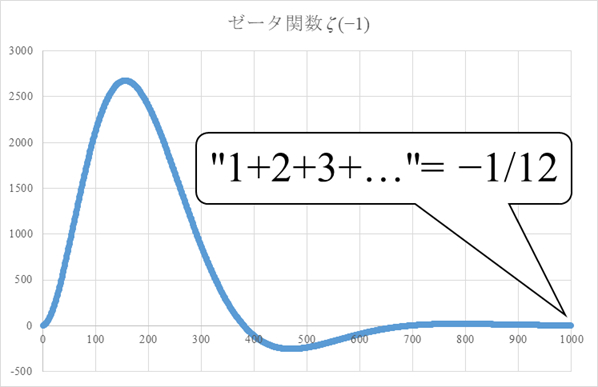
図 3-6: 自然数和の減衰振動
オイラーは1749年に次の式を示唆しました。
"1+2+3+4+…" = −1/12
これはとても不思議な式です。なぜ無限大に発散しないのでしょうか?
オイラー、リーマン、ラマヌジャンが、この式を導きました。その式の秘密を知りたいと思っている方に、ぜひ、この記事を読んでほしいと思います。
要旨は次のとおりです。
(1) 通常の自然数和 1+2+3+4+…は無限大に発散する。
(2) 非常にゆっくり減衰振動する新しい自然数和 ”1+2+3+4+…+n” を定義する。
(3) 有限項では、通常の自然数和 1+2+3+4+…+n と一致する。
(4) 無限項では、 −1/12 に収束する。
上記の説明だけでは減衰振動の仕組みがわからないと思います。その仕組みを理解していただくため、この記事では、もっとも簡単な例から始め、順に説明したいと思います。
目次
6.4 4番目の見解:減衰振動を伴う”1+2+3+…”=−1/12
この記事では、次の公式が成立する理由を説明します。
(自然数の総和公式)
|
|
(1.1) |
複雑な形を理解する方法の一つは、できるだけ単純な形から始め、少しずつ複雑な形に変えていくことです。本論でもそのように進めたいと思います。
次のような、等比数列の項の総和を等比級数といいます。
|
|
(2.1) |
いったい、いくらになるでしょうか?
それは、次のグラフの面積となります。
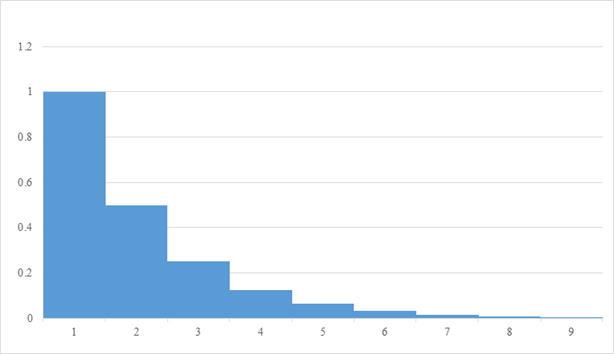
図 2-1: 等比級数
このグラフだと、いくらに収束するか、よくわかりません。
そこで、次の図で考えてみましょう。
図 2-2: 等比級数
上の図を見ると、2に収束しそうです。等比級数はどのように計算すればよいでしょうか?
次のように計算します。
|
|
(2.2) |
|
|
(2.3) |
|
|
(2.4) |
SからS/2を引くと次のようになります。
|
|
(2.5) |
|
|
(2.6) |
|
|
(2.7) |
|
|
(2.8) |
この結果から、公比rの等比級数の公式を得ます。
(等比級数の公式)
|
|
(2.9) |
|
|
(2.10) |
上記の公式は、最終項の極限がゼロの場合に成立します。
次のような、項の正負が交互に入れ替わる等比級数を交代等比級数といいます。
|
|
(2.11) |
次のグラフの面積となります。
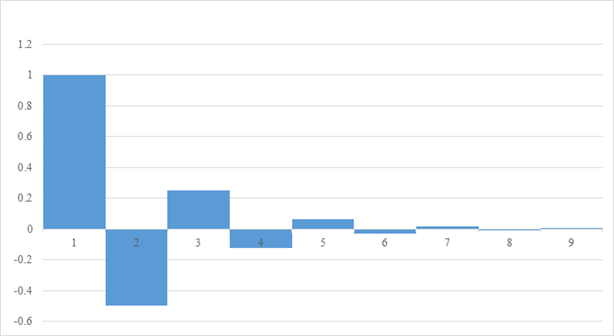
図 2-3: 交代等比級数
このグラフだと、いくらに収束するか、よくわかりません。
そこで、次の図で考えてみましょう。
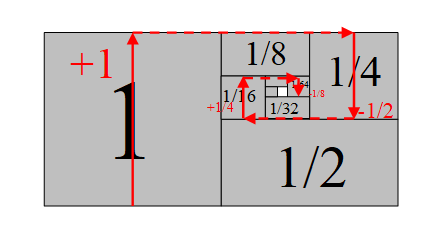
図 2-4: 交代等比級数
赤い矢印の経路において、底辺からの高さが交代等比級数の値となります。上の図を見ると、2/3に収束しそうです。交代等比級数はどのように計算すればよいでしょうか?
次のように計算します。
|
|
(2.12) |
|
|
(2.13) |
|
|
(2.14) |
Sから−S/2を引くと次のようになります。
|
|
(2.15) |
|
|
(2.16) |
|
|
(2.17) |
|
|
(2.18) |
この結果から、次の等比級数の公式における公比rの範囲を拡張できることがわかります。
(等比級数の公式)
|
|
(2.19) |
|
|
(2.20) |
2.3 公比1の交代等比級数
次の公比1の交代等比級数を考えてみましょう。
|
|
(2.21) |
この級数はグランディ級数と呼ばれることがあります。
次のグラフの面積となります。
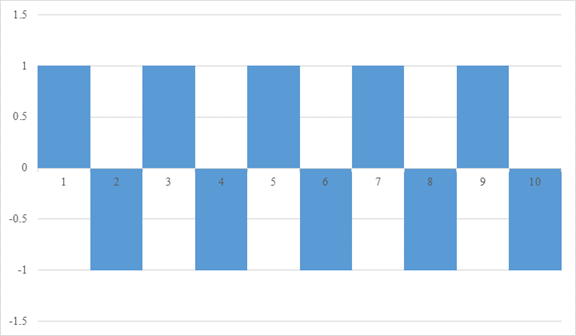
図 2-5: 公比1の交代等比級数
上記の式を次のように解釈します。
|
|
(2.22) |
同様に等比級数の公式を使うと次の式になります。
|
|
(2.23) |
しかし、−1は等比級数の公比の範囲外です。また、級数の最終項の極限がゼロではありません。
最終項は1か−1なので、答えは1か0のはずです。なぜ1/2なのでしょうか?
そこで、次の新しい級数を定義してみましょう。
|
|
(2.24) |
|
|
(2.25) |
変数xはとても小さな正の実数です。有限項nではxを0にすると次の等比級数と等しくなります。
|
|
(2.26) |
|
|
(2.27) |
この等比級数は、非常にゆっくりと減衰し、振動します。
減衰を誇張して描くと、次のグラフの面積となります。
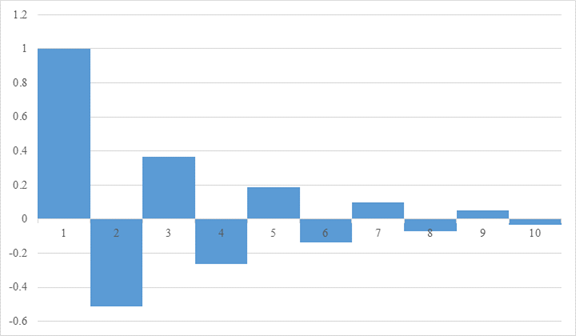
図 2-6: 減衰する公比1の交代等比級数
もう一度、等比級数の公式を書いてみましょう。
|
|
(2.28) |
この最後の結果の変数xに0を入れると1/2が得られます。
|
|
(2.29) |
減衰していくので、最後の項は0です。
この結果から、次の等比級数の公式における公比rの範囲を拡張できることがわかります。
(等比級数の公式)
|
|
(2.30) |
|
|
(2.31) |
公比1の交代等比級数は、減衰振動によって収束しました。減衰振動は、収束しない級数を収束させることができます。
2.4 公比1の等比級数
次の公比1の等比級数を考えてみましょう。
|
|
(2.32) |
次のグラフの面積となります。
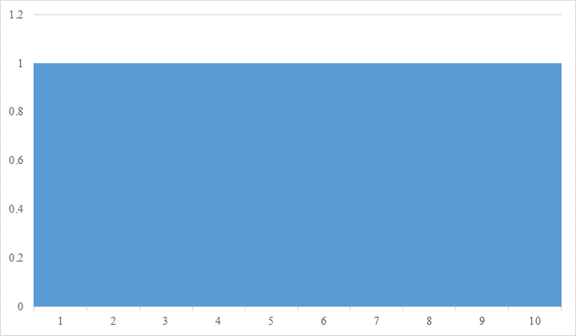
図 2-7: 公比1の等比級数
この級数を考察するため、最初に、正しくない計算方法を説明します。
上記の級数から次の振動級数を引きます。
|
|
(2.33) |
すると次のようになります。(この計算方法は正しくありません)
|
|
(2.34) |
この式を、次のように変形します。
|
|
(2.35) |
つまり、次のようになります。(この計算方法は正しくありません)
|
|
(2.36) |
したがって、次の式が成立します。
|
|
(2.37) |
A は1/2ですので次の式が成立します。
|
|
(2.38) |
しかし、この級数の最終項の極限はゼロではありません。
そのため、上記の計算方法は正しくありません。
そこで、次の級数を定義してみましょう。
|
|
(2.39) |
|
|
(2.40) |
この等比級数は、非常にゆっくりと減衰していきます。
等比級数の公式を書いてみましょう。
|
|
(2.41) |
この最後の結果のxに0を入れると発散します。
|
|
(2.42) |
減衰するだけでは、うまくいきません。この公比1の等比級数は発散しています。どうすれば、よいでしょうか?
前節で、減衰振動は、収束しない級数を収束させました。そのため、減衰振動は発散級数を収束できるかもしれません。
そこで、この公比1の等比級数が実は、非常に長い周期で振動しているとしましょう。そうすれば、無限大を打ち消すことができるかもしれません。
そこで、次のように定義してみましょう。
(減衰振動する公比1の等比級数)
|
|
(2.43) |
|
|
(2.44) |
変数xは、小さな数ですが、この数の効果で非常にゆっくりと振動します。
この結果、次の式が成立します。
(自然数の総和公式)
|
|
(2.45) |
この結果を信じられないかもしれません。そこで次の節で数値計算します。
減衰振動を誇張して描くと次のグラフとなります。
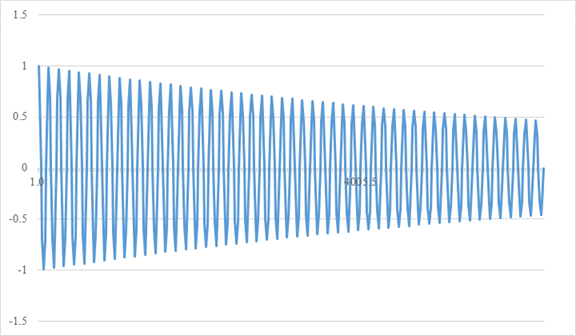
図 2-8: 減衰振動する公比1の等比級数
上記のグラフの計算式は下記です。
|
|
(2.46) |
この結果を、オンライン計算機Wolfram Alphaで確認してみましょう。次のURLをクリックしてみてください。
https://www.wolframalpha.com/input/?i=
sum_{k=1}^infty exp(-0.05^3 k) cos(0.05 k)
同じ結果が得られたと思います。
変数xが0.0001の場合も、オンライン計算機Wolfram Alphaで確認してみましょう。次のURLをクリックしてみてください。
http://www.wolframalpha.com/input/?i=
sum_{k=1}^infty exp(-k*0.0001^3) cos(k*0.0001)
次の結果が得られたと思います。
|
|
(2.47) |
こうして、変数xにより、非常に長い周期で振動します。そして変数xで、さらにゆっくりと減衰します。その結果、次の式が成立するのです。
|
|
(2.48) |
自然数を係数に持つ次の等比級数を考えてみましょう。
|
|
(3.1) |
この小論では、この級数を短く「自然数の等比級数」と呼ぶこととします。
次のグラフの面積となります。
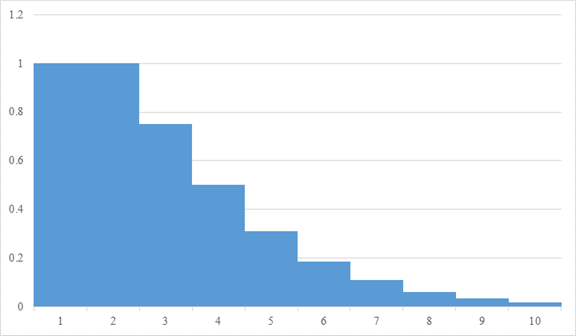
図 3-1: 自然数の等比級数
いったい、いくらになるでしょうか?
次のように計算します。
|
|
(3.2) |
両辺を二乗します。
|
|
(3.3) |
右辺を展開します。
|
|
(3.4) |
|
|
(3.5) |
|
|
(3.6) |
ここで、 1, 1/2, 1/4, 1/8 の項を、それぞれまとめます。
|
|
(3.7) |
|
|
(3.8) |
一方、Sを次のように計算します。
|
|
(3.9) |
|
|
(3.10) |
したがって、S2は次のように計算できます。
|
|
(3.11) |
|
|
(3.12) |
この結果から、次の自然数の等比級数の公式を得ます。
(自然数の等比級数の公式)
|
|
(3.13) |
|
|
(3.14) |
自然数を係数に持つ次の交代等比級数を考えてみましょう。
|
|
(3.15) |
この小論では、この級数を短く「自然数の交代等比級数」と呼ぶこととします。
次のグラフの面積となります。
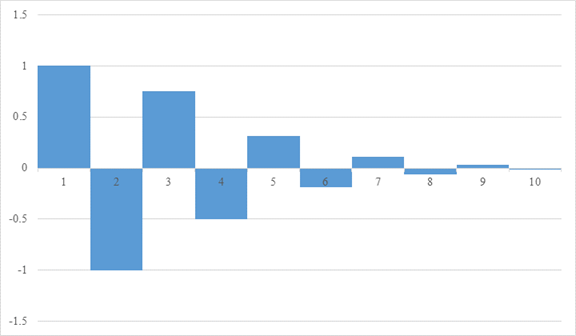
図 3-2: 自然数の交代等比級数
いったい、いくらになるでしょうか?
次のように計算します。
|
|
(3.16) |
両辺を二乗します。
|
|
(3.17) |
右辺を展開します。
|
|
(3.18) |
|
|
(3.19) |
|
|
(3.20) |
ここで、 1, 1/2, 1/4, 1/8 の項を、それぞれまとめます。
|
|
(3.21) |
|
|
(3.22) |
一方、Sを次のように計算します。
|
|
(3.23) |
|
|
(3.24) |
したがって、S2は次のように計算できます。
|
|
(3.25) |
|
|
(3.26) |
この結果から、次の自然数の等比級数の公式における公比rの範囲を拡張できることがわかります。
(自然数の等比級数の公式)
|
|
(3.27) |
|
|
(3.28) |
次のような、自然数の交代級数を考えてみましょう。
|
|
(3.29) |
次のグラフの面積となります。
図 3-3: 自然数の交代級数
上記のような自然数の交代級数を次のように解釈します。
|
|
(3.30) |
同様に自然数の等比級数の公式を使うと次の式になります。
|
|
(3.31) |
しかし、−1は等比級数の公比の範囲外です。また、最終項の極限はゼロではなく、無限大かマイナス無限大です。なぜ1/4なのでしょうか?
そこで、次のように定義してみましょう。
|
|
(3.32) |
|
|
(3.33) |
この自然数の等比級数は、最初増大します。しかし、最終的には指数関数の効果により非常にゆっくりと減衰していきます。
減衰を誇張して描くと、次のグラフの面積となります。
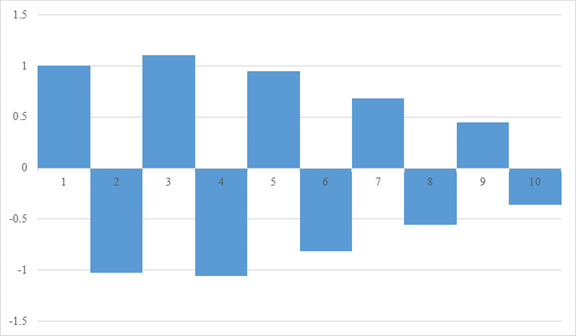
図 3-4: 減衰する交代級数
もう一度、自然数の等比級数の公式を書いてみましょう。
|
|
(3.34) |
この最後の結果のxに0を入れると1/4が得られます。
|
|
(3.35) |
減衰していくので、最終項の極限は0です。
この結果から、次の自然数の等比級数の公式における公比rの範囲を拡張できることがわかります。
(自然数の等比級数の公式)
|
|
(3.36) |
|
|
(3.37) |
自然数の交代級数は、減衰振動によって収束しました。減衰振動は、発散級数を収束させることができます。
次の自然数の級数を考えてみましょう。
|
|
(3.38) |
次のグラフの面積となります。
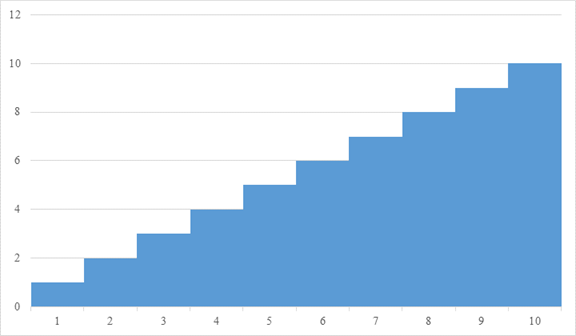
図 3-5: 自然数の級数
この級数を考察するため、最初に、正しくない計算方法を説明します。
上記の級数から次の自然数の交代級数を引きます。
|
|
(3.39) |
すると次のようになります。(この計算は正しくありません)
|
|
(3.40) |
これを、次のように変形します。
|
|
(3.41) |
つまり、次のようになります。(この計算は正しくありません)
|
|
(3.42) |
したがって、次の式が成立します。
|
|
(3.43) |
A は1/4ですので次の式が成立します。
|
|
(3.44) |
しかし、この級数の最終項の極限はゼロではありません。そのため、上記の計算方法は正しくありません。
そこで、次の級数を定義してみましょう。
|
|
(3.45) |
|
|
(3.46) |
この自然数の等比級数は、最初増大しますが、最終的には、非常にゆっくりと減衰していきます。
自然数の等比級数の公式を書いてみましょう。
|
|
(3.47) |
この最後の結果のxに0を入れると発散します。
|
|
(3.48) |
減衰するだけでは、うまくいきません。この自然数の等比級数は発散しています。どうすれば、よいでしょうか?
前節で、減衰振動は、発散級数を収束させました。そのため、減衰振動は自然数の等比級数を収束できるかもしれません。
そこで、この自然数の等比級数が実は、非常に長い周期で振動しているとしましょう。そうすれば、無限大を打ち消すことができるかもしれません。
そこで、次の級数を定義してみましょう。
(減衰振動する自然数の等比級数)
|
|
(3.49) |
|
|
(3.50) |
変数xは、小さな数ですが、この数の効果で非常にゆっくりと振動します。
この結果、次の式が成立します。
(自然数の総和公式)
|
|
(3.51) |
この結果を信じられないでしょう。そこで次の節で数値計算します。
減衰振動を誇張して描くと次のグラフとなります。
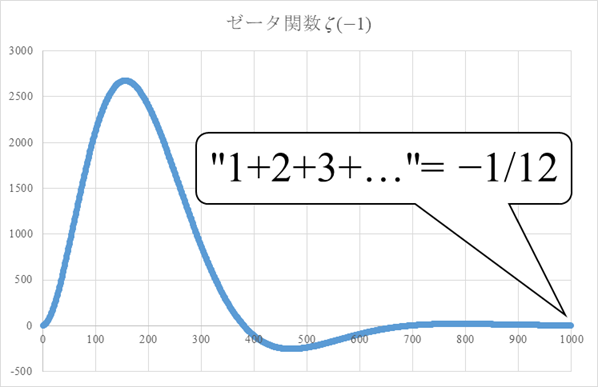
図 3-6: 自然数和の減衰振動
上記のグラフの計算式は下記です。
|
|
(3.52) |
この値は、次の−1/12と非常に近い値です。
|
|
(3.53) |
この結果を、オンライン計算機Wolfram Alphaで確認してみましょう。次のURLをクリックしてみてください。
https://www.wolframalpha.com/input/?i=
sum k exp(-k 0.01) cos(k 0.01), k=1 to 3000
同じ結果が得られたと思います。
私は、自然数和が−1/12に連続的に変化していく途中の様子を観察したいと考えていました。上記の図 3-6では実際に、自然数和が−1/12に変化する様子を観察できます。
変数xが0の極限の場合の結果も、オンライン計算機Wolfram Alphaで確認してみましょう。次のURLをクリックしてみてください。
http://www.wolframalpha.com/input/?i=
lim_{x→0+}sum_{k=1}^infty
k exp(-kx) cos(kx)
次の結果が得られたと思います。
|
|
(3.54) |
こうして、変数xにより、非常に長い周期で振動します。そして、変数xで、ゆっくりと減衰します。その結果、次の式が成立するのです。
(自然数の総和級数の公式)
|
|
(3.55) |
その仕組みは次の論文で説明しています。
・自然数の総和がゼータ関数の−1/12であることの新しい証明
https://xseek-qm.net/Regularization.htm
この結果に対して次のような意見をお持ちの方もいらっしゃると思います。
次の二式は異なる式である。だから、異なる計算結果を与えるのは当然だ。
|
|
(3.56) |
|
|
(3.57) |
|
|
(3.58) |
確かに異なる式です。しかし、変数xは非常に小さい数です。そのため、項数が有限個の場合、上記の二つの式は一致します。
|
|
(3.59) |
|
|
(3.60) |
|
|
(3.61) |
しかし、無限項では次のようになります。
|
|
(3.62) |
|
|
(3.63) |
次の級数は発散します。
|
|
(4.1) |
ここで、次の級数を定義します。
|
|
(4.2) |
|
|
(4.3) |
有限項では次のように一致します。
|
|
(4.4) |
しかし、無限項では次のようになります。
|
|
(4.5) |
|
|
(4.6) |
補足では、参考となる情報をまとめます。
レオンハルト・オイラー[1]は1749年に次の関数等式を発見し1768年に発表しました。
上記の式より次の式が得られます。
(自然数の総和公式)
|
|
(5.3) |
実際には、オイラーは式(5.3)を明確に書きませんでした。そのため、オイラーが級数の和を−1/12としたかについては、実ははっきりしていません。
式(5.3)の求め方は次の通りです。
式(5.1)のnに2を代入し次の式を得ます。
|
|
(5.4) |
上記の式を計算し次の式を得ます。
|
|
(5.5) |
右辺の括弧の中はバーゼル問題よりπ2/6です。
|
|
(5.6) |
上記の式(5.6)を式(5.5)に代入します。
|
|
(5.7) |
|
|
(5.8) |
上記の結果は後で使います。
次に、式(5.2)のnに2を代入し次の式を得ます。
|
|
(5.9) |
右辺を次のように計算します。
|
|
(5.10) |
|
|
(5.11) |
|
|
(5.12) |
|
|
(5.13) |
従って、式(5.9)は次のように書けます。
|
|
(5.14) |
左辺の分母を両辺にかけ、次の式を得ます。
|
|
(5.15) |
上記の式を計算します。
|
|
(5.16) |
右辺の括弧の中は式(5.8)よりπ2/12です。
|
|
(5.17) |
計算し次の式を得ます。
|
|
(5.18) |
オイラーは上記の式(5.18)までは、認識していました。
次に、式(5.1)のnに−1を代入し次の式を得ます。(nに−1を代入することをオイラーが想定していたかどうかは定かでありません)
|
|
(5.19) |
上記の式を計算し次の式を得ます。
|
|
(5.20) |
|
|
(5.21) |
|
|
(5.22) |
|
|
(5.23) |
上記の式の左辺に、式(5.18)を代入します。
|
|
(5.24) |
両辺に−1/3をかけ、左辺と右辺を入れ替えると次の式を得ます。
|
|
(5.25) |
オイラーが上記の式を認識していたかどうかは定かではありません。
リーマン[2]は1859年に次のゼータ関数を定義しました。
(リーマンのゼータ関数の級数定義式)
|
|
(5.26) |
そして、次の関数等式を示しました。
|
|
(5.27) |
この関数等式を使うことで、ゼータ関数の引数の領域を延長できます。
このように、関数の引数の領域を延長することを「解析接続する」といいます。
上記の式より次の式が得られます。
(自然数の総和公式)
|
|
(5.28) |
ラマヌジャン[3]は1913年に次の式を示しました。
(自然数の総和公式)
|
|
(5.29) |
級数の最終項の極限がゼロではないため、正しい計算方法ではありませんが、ラマヌジャンによる発散級数の計算方法は次のとおりです。
次の値をSとおきます。
|
|
(5.30) |
上記の式を4倍します。
|
|
(5.31) |
|
|
(5.32) |
次のように、Sから4Sを引きます。(この計算方法は正しくありません)
|
|
(5.33) |
一方、次の式が成立します。
|
|
(5.34) |
したがって、次の式が成立します。
(自然数の総和公式)
|
|
(5.35) |
ラマヌジャンが上記の正しくない計算方法を使った理由は、彼が彼独自の方法で同じ結果を得ていたためだと思います。
彼はその結果を得るために、オイラー=マクローリンの総和公式を使いました。
(オイラー=マクローリンの総和公式)
|
|
(5.36) |
上記の公式の誤差項(剰余項) Rmは次の通りです。
|
|
(5.37) |
上記の多項式 Bm(x) はベルヌーイ多項式です。
オイラー=マクローリンの総和公式を簡潔に表現するため、ベルヌーイ数B1の定義を−1/2から1/2に変更します。
|
|
(5.38) |
さらに、積分を次の記号で定義します。
|
|
(5.39) |
すると、オイラー=マクローリンの総和公式は次のように簡潔に表現できます。
(オイラー=マクローリンの総和公式)
|
|
(5.40) |
さらに関数f (k)を、自然数mが無限大になる時、誤差項Rmが0になるような関数と仮定します。
すると自然数mが無限大となる条件で、オイラーマクローリンの総和公式は次のように表現できます。
(オイラー=マクローリンの総和公式)
|
|
(5.41) |
ラマヌジャンは上記の式を自然数nに依存する項Cnと、自然数nに依存しない定数Cに分離しました。
|
|
(5.42) |
|
|
(5.43) |
|
|
(5.44) |
発散級数の値に上記の定数項Cを割り当てる方法をラマヌジャン総和法と呼びます。
ここで関数f (k)が自然数の場合を考えます。
|
|
(5.45) |
すると自然数和は次のように書けます。
|
|
(5.46) |
|
|
(5.47) |
|
|
(5.48) |
したがって、ラマヌジャン総和法により、自然数和は−1/12となります。
しかし、自然数nに依存する項Cnを無視して良い理由は、よくわかりません。
ゼータ関数ζ(−1) = “1+2+3+…”について次のような見解があるようです。
この小論では4番目の見解を主張しました。
6.1 1番目の見解:1+2+3+…=∞
ゼータ関数における自然数の級数について、次のように主張する人がいます。
解析接続の観点で、次の式の左辺は、−1/12と等しい。
|
|
(6.1) |
一方、次の式の左辺は、右辺と等しくない。
|
|
(6.2) |
次の式の左辺は発散し、無限大となる。
|
|
(6.3) |
しかし私は、なんとかしてゼータ関数における自然数の級数を理解したいと考え、この小論をまとめました。
6.2 2番目の見解:1+2+3+…=−1/12
ゼータ関数における自然数の級数について、次のように主張する人がいます。
解析接続の観点で、次の式の左辺は、−1/12と等しい。
|
|
(6.4) |
一方、ゼータ関数は次のように表現できる。
|
|
(6.5) |
したがって、次の式の左辺は、−1/12と等しい。
|
|
(6.6) |
しかし、どのようにすれば、そうなるのでしょうか?
6.3 3番目の見解:“1+2+3+…”=−1/12
ゼータ関数における自然数の級数について、次のように主張する人がいます。
解析接続の観点で、次の式の左辺は、−1/12と等しい。
|
|
(6.7) |
一方、ゼータ関数は次のように「解釈」できる。
|
|
(6.8) |
したがって、次の式の左辺は、−1/12と等しいと「解釈」できる。
|
|
(6.9) |
しかし、その「解釈」とは何を意味するのでしょうか?
6.4 4番目の見解:減衰振動を伴う”1+2+3+…”=−1/12
ゼータ関数における自然数の級数に対する、この小論の主張は次のとおりです。
次の式の左辺は、発散し無限大となる。
|
|
(6.10) |
二重引用符で囲んだ特殊な自然数和を次のように定義する。
|
|
(6.11) |
|
|
(6.12) |
特殊な自然数の有限和は、通常の自然数和に等しい。
|
|
(6.13) |
一方、特殊な自然数の無限和は、−1/12に等しい。
|
|
(6.14) |
この定義により、通常の自然数和が徐々に−1/12へ近づく様子を観察できます。