虚数とは、2回の変換で、画像を拡大し180度回転する変換です。
次の記事で、虚数の行列表現を説明します。
• なぜ虚数単位iの2乗は-1になるのか?[2014/6/29]私が初めて虚数を学んだとき、とても悩みました。
$$ i^2 = -1 $$2乗して-1になる実数は存在しません。 そのため、虚数の存在を仮定することに大きな違和感を覚えました。 このような奇妙な数を定義したら、どこかで矛盾が生じるのではないかと思いました。 しかし、どこまで行っても矛盾はまったく現れません。 むしろ必要なピースが埋まったパズルのように、うまくいくのでした。 そのため私は別の疑問をもち始めました。
「ありえない数を仮定して、これほどうまくいくのはなぜなのだろう?」
そのような疑問をもち悶々としていましたが、ある日、私はある数学の問題に出会いました。 その問題は次の行列を定義していました。
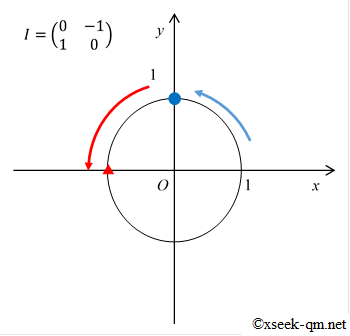
$$ I = \left(\begin{array}{cc} 0 & -1 \\ 1 & 0 \\ \end{array}\right) $$この行列 I を虚数の行列表現といいます。 この行列 I の演算は虚数 i とまったく同じになります。 たとえば、次の式が成立します。
$$ I^2 = -E $$私は、この問題に出会い、次のように解釈しました。
「虚数の記号 i は、行列 I の略記なのだ」
「虚数が行列の略記である」という文の意味を説明します。 たとえば、次のような二次方程式に出会ったとします。
$$ x^2-2x + 2 = 0 $この方程式を、次のような行列 X の方程式と解釈します。
$$ X^2-2X + 2E = 0 $$そうすると、次の解が自然に得られます。
$$ X=E \pm I $$この解を次の解と解釈するのです。
$$ x=1 \pm i $$そのように解釈することで、私の疑問は氷解しました。 私は納得することができました。
複素数は、二次方程式の視点では説明しないほうがよいと、私は思います。 二次方程式の視点で虚数を見ると、 どうしても「虚数は存在しない数」という印象をもってしまいます。 虚数は行列の視点で説明したほうがよいと、私は思います。 二次方程式の視点で虚数を見れば、 数の2乗が-1になることは、まったく起こりえない現象です。 一方、行列の視点で虚数を見れば、 2乗して負の単位行列 -E になることは十分に起こりえる現象です。
そこで、行列から複素数を案内する次の記事を作りました。 記事では、先ほどの行列 I を「虚数単位行列」または 「回転単位行列」と呼んでいます。
その記事の目的は、私のように虚数で悩む人を減らすことです。 記事は行列の知識を必要としています。 そのため、記事の対象となる読者は、行列を学んだ方々となります。
私が初めて行列を学んだとき、行列の演算規則がとても奇妙に感じました。 行列の利用方法がわからないまま、ただひたすら行列の計算を練習しました。 その後、行列は一次変換に使えることがわかりました。 行列を説明するときは、 「行列は一次変換の略記である」と説明したほうがよいと私は思います。 そうすれば、行列の奇妙な演算規則はとても自然に思えるはずです。
行列は図で表現できないため、幾何学的に想像できません。 そこで、単位円が行列でどのように変換されるかを図示してみました。 単位円は行列で次のように変換されます。
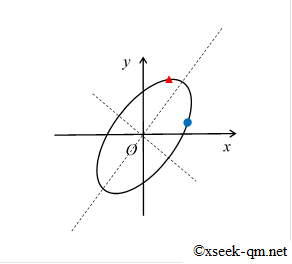
青い丸印が座標(1,0)の移動先です。赤い三角印が、座標(0,1)の移動先です。 上記の図を見ると、楕円の主軸が固有ベクトルのように見えます。 しかし、常にそうではありません。 一般的に、主軸は次の図のように固有ベクトルと異なります。
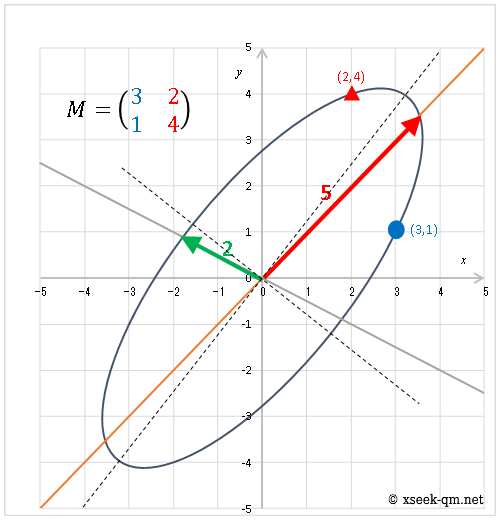
その記事の最後に述べる特異値分解は行列の理解に役立つと思います。 特異値分解により、一般の行列を、右回転、横拡大、縦拡大、左回転に分解できます。
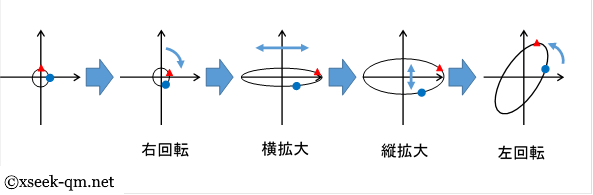
任意の行列を楕円として解釈すれば、行列を視覚的に観察できます。 目に見えない行列が目で見えることの恩恵は大きいと思います。
ある数の存在は背理法で否定できます。 たとえば、次のように表現します。
「ある数の存在を仮定し矛盾が生じるならば、その数は存在しない」
この背理法の対偶を取ってみましょう。
「ある数が存在するならば、その数の存在を仮定しても矛盾は生じない」
虚数の存在を仮定しても矛盾は生じないので、虚数は存在するといえるような気がします。 しかし、よく考えてみると、これは結論から前提条件を導いています。 論理的に正しくありません。 虚数に矛盾がないからといって、虚数が存在するとは限らないのです。
感覚的にも、数の2乗が-1になることはありえません。 そのため、どうも腑に落ちません。 なぜ、これほどまでに感覚に反するのでしょうか?
腑に落ちないという感覚を軽減する方法がひとつあります。 それは虚数を「回転単位行列の略記」と解釈する方法です。

回転単位行列とは、画像を回転する行列です。私たちは、日常的に画像を回転します。 そのため、回転操作の存在を疑うことはないと思います。 虚数とは実は回転変換のことなのです。 虚数が回転変換の略記ならば、 虚数の存在を感覚的に認められるのではないでしょうか?
虚数という名前には、「本当は実在しない、空想上の数」、という印象があります。 しかし、このページで説明したとおり、虚数は回転変換です。 回転変換が実在するのと同じぐらいしっかりと、虚数は実在しています。 「虚数は実在しない」という誤解を与えないため、 私は虚数の新しい名前を提案したいと思います。
まず、虚数を「数」と呼ぶこと自体が誤解の原因だと思います。 「数」という言葉は、日常的には「物体の個数」を意味します。 それは自然数です。 これまで数学の世界では「数」という言葉の意味を何度も拡張してきました。 しかし、言葉の意味を拡張すればするほど、その言葉の意味はどんどん希薄になっていきます。
整数は「物体の位置」と解釈できるでしょう。 実数は「物体の長さ」と解釈できるでしょう。 それらは、「数」という言葉の意味を拡張することで、「数」と呼ぶことができます。 でも虚数は違います。 それは、もはや「数」と呼ぶべきではありません。 それは、回転変換の単位と呼ぶべきものです。 私は虚数の新しい名前として、回転変換単位、または短く回転単位を提案します。
現在、教科書では虚数を次のように教えています。
「2乗して-1になる数を虚数単位と呼ぶ」
「そんな数は存在しないよ!」、と普通の人は思うはずです。 そこで、次のように教えてはどうでしょうか?
「2回の変換で、画像を180度回転する変換を回転変換単位、または回転単位と呼ぶ」
「そんな変換は存在しないよ!」、と思う人はいないはずです。 むしろ、「その変換は二種類存在するな!」、と洞察するのではないでしょうか? その二種類の変換とは、 +i と -i のことです。 生徒に、そのような洞察を与えるほど、その学習効果は高いと思います。
私は、名前というものをとても大切だと思っています。 たとえその名前が数学的に正確でなかったとしても、わかりやすい名前をつければ、 数学の好きな人が増えるのではないでしょうか?
© 2014-2015 xseek-qm.net
広告


