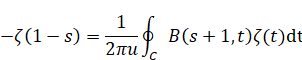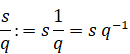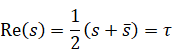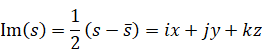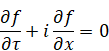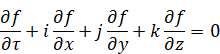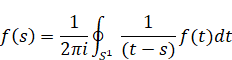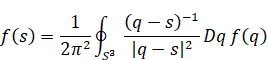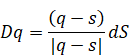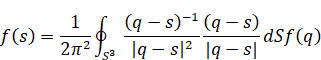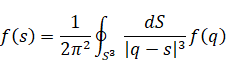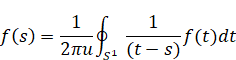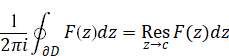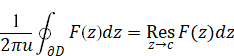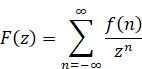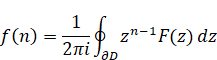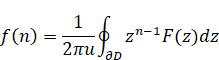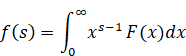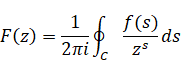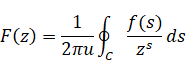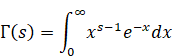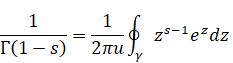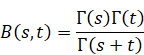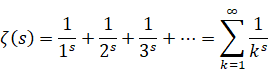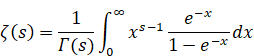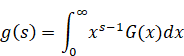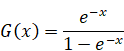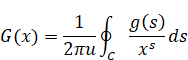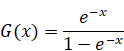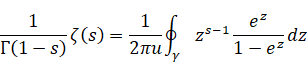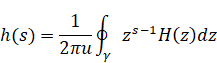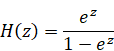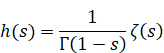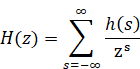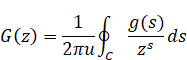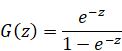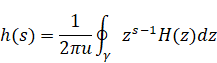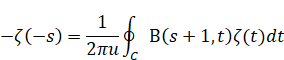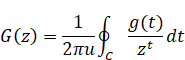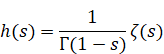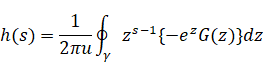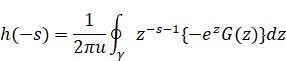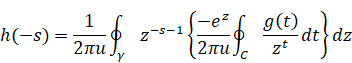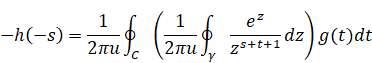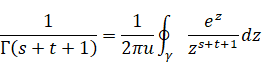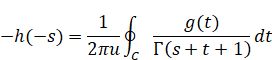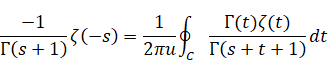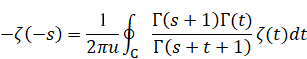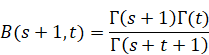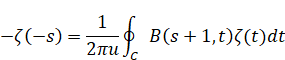四元数解析によるゼータ関数の反射積分方程式の導出
ホーム > 量子力学 > ゼータ関数とベルヌーイ数
2019/03/04
公開日 2014/5/18
K. Sugiyama[1]
四元数解析でゼータ関数の反射積分方程式を導出する。
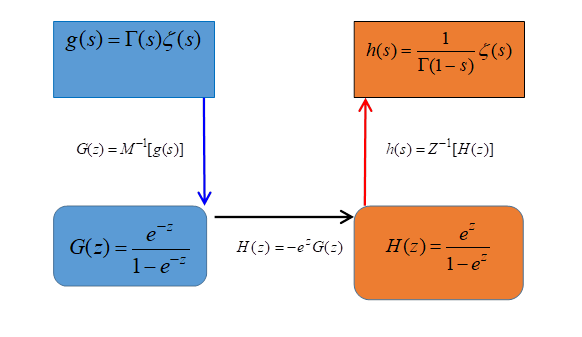
図 3-1: 導出方法の枠組み
多くの研究者が、リーマン予想の証明を試みてきたが、成功していない。このリーマン予想の証明は数学の重要な課題となっている。本論文では、リーマン予想を証明する準備として、四元数解析から、反射積分方程式の導出を試みる。
メリン逆変換より、ある母関数を得る。その母関数を指数倍し、その符号を反転することで、新しい母関数を得る。その母関数を逆Z変換し反射積分方程式を導出する。
目次
1 序論
1.1 課題
多くの研究者が、リーマン予想の証明を試みてきたが、成功していない。このリーマン予想の証明は数学の重要な課題となっている。本論文では、リーマン予想を証明する準備として、四元数解析から、反射積分方程式の導出を試みる。
1.2 課題の重要性
リーマン予想の証明は、数学における最も重要な未解決問題の一つである。
このため、多くの数学者がリーマン予想の証明を試みてきた。しかし、それらの試みは成功していない。リーマン予想を証明する方法の一つは、ゼータ関数の零点を、ある作用素の固有値と解釈することである。しかし、これまで、その作用素は見つかっていなかった。反射積分方程式は、この作用素のひとつと考えられる。このため、反射積分方程式の導出は重要な課題である。
1.3 これまでの研究動向
レオンハルト・オイラーは、1737年にゼータ関数を導入した。ベルンハルト・リーマンは1859年に、その関数の引数を複素数に拡大した。
ダフィット・ヒルベルトとゲオルグ・ポリア[2]は1914年頃に、その関数の零点は、ある作用素の固有値であろうと予想した。この予想はヒルベルト=ポリア予想と呼ばれている。
ゼエフ・ルドニックとピーター・サルナック[3]は1996年にランダム行列理論で零点の分布を研究している。黒川重信氏は1996年頃より1元体[4]を研究している。アラン・コンヌ[5]は1998年に非可換幾何学とリーマン予想の関係を示した。クリストファー・デニンガー[6]は1998年に零点の固有値解釈を研究している。
1.4 本論文の新しい導出方法
メリン逆変換より、ある母関数を得る。その母関数を指数倍し、その符号を反転することで、新しい母関数を得る。その母関数を逆Z変換し反射積分方程式を導出する。
(四元数の反射積分方程式)
|
|
(1.1) |
変数uは、単位四元数i, j, kで構成される新しい単位四元数である。
|
|
(1.2) |
|
|
(1.3) |
2 既知の内容の確認
本章では、既知の内容を確認する。
2.1 四元数
オイラーは1748年ごろに複素数を利用した。
|
|
(2.1) |
ウィリアム・ローワン・ハミルトン[7]は、1843年に四元数を発表した。
|
|
(2.2) |
四元数を次のように定義する。
|
|
(2.3) |
|
|
(2.4) |
四元数の割り算の順序を次のように定義する。
(四元数の割り算の順序)
|
|
(2.5) |
四元数共役を次のように定義する。
|
|
(2.6) |
四元数関数を次のように定義する。
|
|
(2.7) |
絶対値の二乗を次のように定義する。
|
|
(2.8) |
本論文では、次の記号を定義する。
|
|
(2.9) |
|
|
(2.10) |
2.2 四元数解析
オーギュスタン=ルイ・コーシー[8]は1814年に複素解析のため次の方程式を導入した。1851年にリーマン[9]も複素解析のために、この方程式を利用した。
(コーシー=リーマンの微分方程式)
|
|
(2.11) |
フューター[10]は1934年に、四元数解析のため、コーシー=リーマン方程式の類似として、次の方程式を導入した。
(コーシー=リーマン=フューター微分方程式)
|
|
(2.12) |
コーシーは、次の積分公式を導入した。
(コーシーの積分公式)
|
|
(2.13) |
ここでS1は周回経路である。
フューターはコーシーの積分公式の類似として次の公式を導入した。
(コーシー=フューターの積分公式)
|
|
(2.14) |
ここで、S 3は三次元閉曲面である。Dqは次のように定義する。
|
|
(2.15) |
ここでdSは三次元閉曲面S 3上の体積要素である。
上記の式を積分公式に代入し次の式を得る。
|
|
(2.16) |
|
|
(2.17) |
四元数解析の詳細は、1979年のサドベリの論文[11]に記載されている。
上記の式には四元数の絶対値が含まれる。本論文は、四元数の絶対値を含まない次の新しい公式を導入する。
(四元数に対するコーシーの積分公式)
|
|
(2.18) |
ここでS1は四元数空間における積分経路である。
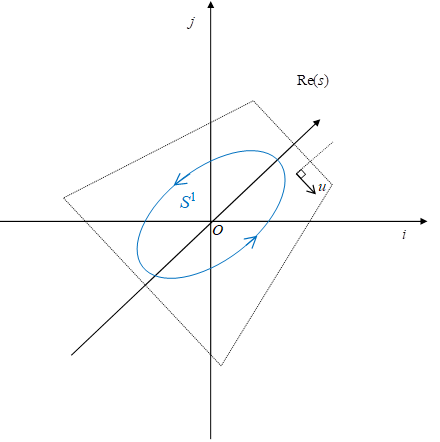
図 2.1: 四元数空間における積分経路S1
本論文は、上記の図において、積分経路S1を含む平面を単位四元数平面と呼ぶ。四元数は非可換だが、単位四元数平面上の四元数は可換である。そのため、単位四元数平面上の積分では四元数の非可換性を無視できる。
変数uは、単位四元数i, j, kで構成される新しい単位四元数である。
|
|
(2.19) |
|
|
(2.20) |
単位四元数平面上の任意の単位四元数qは次のように表現できる。
|
|
(2.21) |
2.3 コーシーの留数定理
オーギュスタン=ルイ・コーシーは、1831年に留数定理[12]を発表した。
関数F (z)が領域Dに孤立特異点cを持つとする。この時、領域Dを囲む単純閉曲線∂Dについて次の式が成立する。
(留数定理)
|
|
(2.22) |
四元数の留数定理を次のように定義する。
(四元数の留数定理)
|
|
(2.23) |
ここで、変数uは単位四元数である。
2.4 フレビッツのZ変換
ビトルド・フレビッツ[13]は1947年にZ変換を発表した。関数F(z)が領域D = {0<|z|<R}で正則ならば、その領域内で広義一様収束する級数に変換できる。
(Z変換)
|
|
(2.24) |
|
|
(2.25) |
|
|
(2.26) |
逆Z変換を次のように定義する。
(逆Z変換)
|
|
(2.27) |
|
|
(2.28) |
四元数の逆Z変換を次のように定義する。
(四元数の逆Z変換)
|
|
(2.29) |
|
|
(2.30) |
ここで、変数uは回転単位四元数である。
2.5 メリン変換
ハジャルマー・メリン[14]は、1904年にメリン変換を発表した。
(メリン変換)
|
|
(2.31) |
|
|
(2.32) |
複素数のメリン逆変換を周回積分で次のように定義する。
(メリン逆変換)
|
|
(2.33) |
|
|
(2.34) |
一方、四元数のメリン逆変換を周回積分で次のように定義する。
(四元数のメリン逆変換)
|
|
(2.35) |
|
|
(2.36) |
ここでCは四元数空間における積分経路である。変数uは回転単位四元数である。
積分経路Cは被積分関数のすべての極を囲む。例として積分経路C を次のようにとる。白丸は極である。
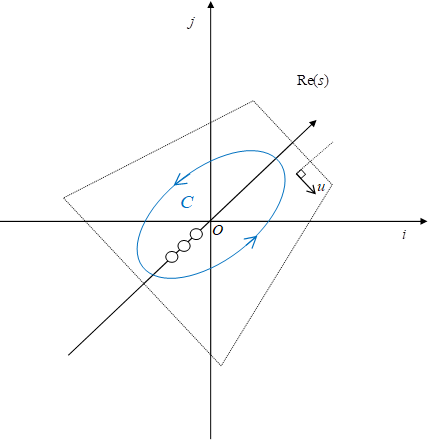
図 2.2: 四元数空間における積分経路C
2.6 オイラーのガンマ関数
レオンハルト・オイラー[15]は1729年に階乗の一般化としてガンマ関数を導入した。
(ガンマ関数の積分定義式)
|
|
(2.37) |
ガンマ関数の四元数の周回積分は次のとおり。
(ガンマ関数の周回積分)
|
|
(2.38) |
ここで、変数uは単位四元数である。
積分経路γを次の図に示す。白丸は極を意味する。
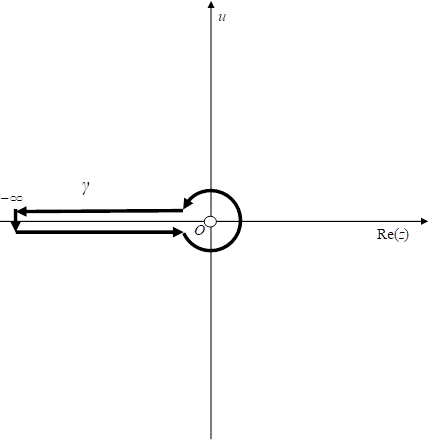
図 2-3: ガンマ関数の積分経路
2.7 オイラーのベータ関数
レオンハルト・オイラーは、1768年に彼の著書[16]でベータ関数を導入した。ベータ関数は次のように、ガンマ関数で表現できる。
(ベータ関数の定義式)
|
|
(2.39) |
2.8 リーマンのゼータ関数
ベルンハルト・リーマン[17]は、1859年にゼータ関数を導入した。
(ゼータ関数)
|
|
(2.40) |
ゼータ関数はガンマ関数で次のように表現される。
(ゼータ関数)
|
|
(2.41) |
上記の式を次のメリン変換と解釈する。
(メリン変換)
|
|
(2.42) |
|
|
(2.43) |
|
|
(2.44) |
|
|
(2.45) |
その関数のメリン逆変換は次のとおりである。
(メリン逆変換)
|
|
(2.46) |
|
|
(2.47) |
|
|
(2.48) |
|
|
(2.49) |
変数uは単位四元数である。
ゼータ関数の解析接続は次のとおりである。
(ゼータ関数の解析接続)
|
|
(2.50) |
上記の式を、次の逆Z変換と解釈する。
(逆Z変換)
|
|
(2.51) |
|
|
(2.52) |
|
|
(2.53) |
|
|
(2.54) |
積分経路γを次の図に示す。白丸は極を意味する。
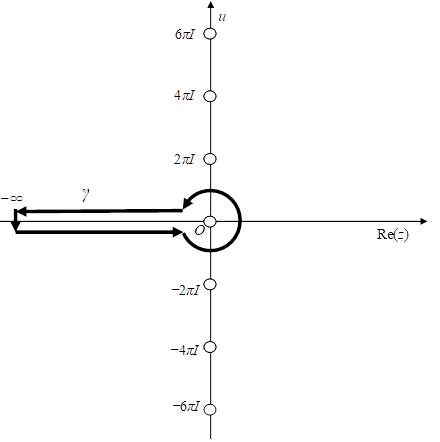
その関数のZ変換は次のとおり。
(Z変換)
|
|
(2.55) |
|
|
(2.56) |
|
|
(2.57) |
|
|
(2.58) |
メリン変換とZ変換の母関数は次の関係を持つ。
|
|
(2.59) |
|
|
(2.60) |
3 反射積分方程式の導出
3.1 導出方法の枠組み
ゼータ関数のメリン逆変換は次のとおり。
|
|
(3.1) |
|
|
(3.2) |
|
|
(3.3) |
|
|
(3.4) |
その関数の逆Z変換は次のとおり。
|
|
(3.5) |
|
|
(3.6) |
|
|
(3.7) |
|
|
(3.8) |
メリン変換とZ変換の母関数は次の関係を持つ。
|
|
(3.9) |
|
|
(3.10) |
導出方法の枠組みは次のとおり。

図 3-1: 導出方法の枠組み
上記の枠組みで、反射積分方程式を得ることができる。
(反射積分方程式)
|
|
(3.11) |
本論文は、この導出方法を説明する。
3.2 ゼータ関数の反射積分方程式の導出
ゼータ関数のメリン逆変換は次のとおり。
|
|
(3.12) |
|
|
(3.13) |
|
|
(3.14) |
|
|
(3.15) |
メリン逆変換では、積分経路Cは被積分関数のすべての極を囲む必要がある。そこで積分経路Cを次のように取る。白丸は極である。
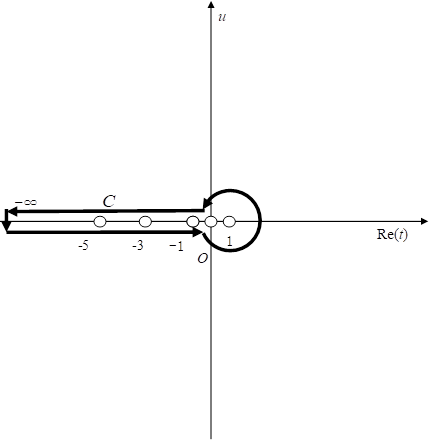
図 3-2: メリン逆変換の積分経路
一方、その関数の逆Z変換は次のとおり。
(逆Z変換)
|
|
(3.16) |
|
|
(3.17) |
|
|
(3.18) |
|
|
(3.19) |
積分経路 γ は次の図のとおり。白丸は極を意味する。
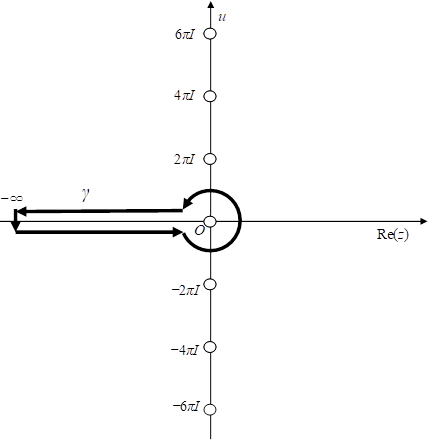
図 3-3: ゼータ関数の積分経路
逆Z変換の式を次のように変形する。
|
|
(3.20) |
上記の式のsを−sに置き変える。
|
|
(3.21) |
上記の式にメリン逆変換の式を代入すると下記式を得る。
|
|
(3.22) |
単位四元数平面上の四元数は可換である。本節では単位四元数平面に存在する変数で積分するため、単位四元数平面上の積分では四元数の非可換性を無視できる。
変数 z について積分するため、次のように式を変形する。
|
|
(3.23) |
上記の式に、次の式を適用する。
(ガンマ関数の周回積分)
|
|
(3.24) |
その結果、次の式を得る。
|
|
(3.25) |
|
|
(3.26) |
|
|
(3.27) |
次のベータ関数を利用して式を簡略化する。
|
|
(3.28) |
すると下記式となる。
(反射積分方程式)
|
|
(3.29) |
上記の式の右辺はs階後退差分のネールント=ライス積分となっている[18]。
積分経路C は次のとおり。白丸は極である。

図 3-4: ゼータ関数の反射積分方程式の積分経路
4 結論
本論文では、次の結果を得た。
・反射積分方程式を導出した。
5 今後の課題
今後の課題は次のとおり。
- 反射積分方程式の固有値を調べる。