マンデルブロ集合とは、次の漸化式で zn が無限大に発散しない複素数 c の集合です。
コスタス・シメオニディス氏のマンデルブロ集合を描画するページをGNUライセンスにもとづいて改変し、 アニメーション機能を追加して次のページを作りました。 マンデルブロ集合の内部は本来ならば黒色ですが、ここでは複素数の値を色で描画しています。
マウスをドラッグし四角形を作れば、その領域を拡大できます。 反復回数とは再帰計算の反復回数です。初期状態の反復回数は16です。 [Start]ボタンを押すと、反復回数が増大するアニメーションを表示します。 反復回数増大に対応してマンデルブロ集合が構成される様子を観察できます。
原点付近のマンデルブロ集合を拡大すると、 次のような画像を見ることができます。
マンデルブロ集合の渦巻きを次のページで見ることができます。
マンデルブロ集合の全景から、画像の場所へアニメーションで降下します。
マンデルブロ集合は、次の漸化式で構成しました。
では、次の指数関数の漸化式でも構成できるでしょうか？
上記の漸化式でも、構成できます。次のページで確認できます。
初期状態の反復回数は4です。 [Start]ボタンを押すと、反復回数が増大するアニメーションを表示します。
原点付近を拡大すると、次のような画像を見ることができます。
指数関数のマンデルブロ集合の渦巻きを次のページで見ることができます。 計算時間が長いため注意願います。
ゼータ関数とは、次の級数で表現される関数です。
$$ \zeta(s)=\frac{1}{1^s} + \frac{1}{2^s} + \frac{1}{3^s} + \cdots $$そのグラフを次のページで確認できます。
画面の描画にはJavaScriptのCanvasとWeb Workersを使用しました。 項数とは計算式の項数です。初期状態の項数は16です。 [Start]ボタンを押すと、項数が増大するアニメーションを表示します。 項数増大に対応して零点が構成される様子を観察できます。
説明：
マンデルブロ集合は、次の漸化式で構成しました。
次のゼータ関数の漸化式でも構成できるでしょうか？
上記の漸化式でも、構成できます。次のページで確認できます。
反復回数の[Start]ボタンを押すと、反復回数が増大するアニメーションを表示します。 項数の[Start]ボタンを押すと、項数が増大するアニメーションを表示します。
ゼータ関数のマンデルブロ集合は、ケンブリッジ大学のウーンが1998年に紹介しています。
零点付近を拡大すると、次のような画像を見ることができます。 計算時間が長いため注意願います。
ゼータ関数のマンデルブロ集合の渦巻きを次のページで見ることができます。 計算時間が非常に長いため注意願います。
上記の画像は花のように見えます。
次の表に示すように、それぞれのマンデルブロ集合にはよく似た画像があります。
| F (z) | z 2 | ez | ζ(z ) |
|---|---|---|---|
| 全景 | |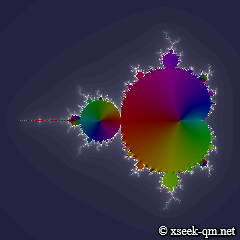
|
|
| 原点 零点 付近 |
|
|
|
| 渦巻 き |
|
|
|
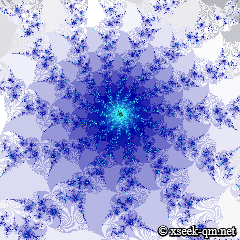私は、次のことが原因だと推測します。
それらの集合の物理的意味とはなんでしょうか？
マンデルブロ集合の一点は、無限に発散するか収束します。 一方、宇宙は、無限に膨張するか収縮します。 マンデルブロ集合のある一点は、ある宇宙と対応しているのではないでしょうか？
次の計算式は収束がよくありません。
$$ \zeta(s)=\frac{1}{1^s} + \frac{1}{2^s} + \frac{1}{3^s} + \cdots $$そのため、次の計算式で計算しています。
各計算式の計算精度は次のページで確認できます。
それぞれの計算式を次節以降で説明します。
オイラーは、オイラー＝マクローリンの和公式でゼータ関数の漸近展開を導入しました。 グラフのページでボタン[ζ_AE]を押せば確認できます。
$$ \zeta_{AE}(s)=\sum_{k=1}^{q-1}\frac{1}{k^s} + \sum_{k=0}^{r} \frac{B_k}{k!}\;\;\frac{\Gamma(s+k-1)}{\Gamma(s)q^{s + k-1}} $$ここで、 Bk はベルヌーイ数です。 本ページではベルヌーイ数として ベルヌーイ多項式の Bk(1) を使用します。 上記の計算式の q が項数です。また、 r = q で計算しています。 項数が14以上、 s の実部が-10以下の領域では計算誤差が大きいため、次の計算式で計算しています。
$$ \zeta(1-s) = \frac{2}{(2\pi)^s}\;\;\Gamma(s)\;\;\cos \Bigl(\frac{\pi}{2}s \Bigr) \; \zeta(s) $$上記の計算式は、数学者リーマンが1859年に発表した関数等式です。 「リーマンの関数等式」と呼ばれています。
クノップは1930年ごろに次の式を予想しました。同式はハッセによって1930年に証明されました。 グラフのページでボタン[ζ_KH]を押せば確認できます。
$$ \zeta_{KH}(s)=\frac{1}{1-2^{1-s}}\sum_{n=0}^q\frac{1}{2^{n + 1}} \sum_{k=0}^{n}{n \choose k}\frac{(-1)^k}{(k + 1)^s} $$項数が27以上で s の実数部分が-7以下の領域では計算誤差が大きいため、 リーマンの関数等式を使用しています。
ピーター・ボールウェインは2000年に次の計算式を発表しました。 グラフのページでボタン[ζ_PB]を押せば確認できます。
$$ \zeta_{PB}(s)=\frac{1}{1-2^{1-s}} \;\;\;\frac{-1}{d_q} \sum_{k=0}^{q-1}(d_k-d_q)\frac{(-1)^k}{(k + 1)^s} $$項数が32以上で s の実数部分が-7以下の領域では計算誤差が大きいため、リーマンの関数等式を使用しています。
©2013, xseek-qm.net
広告
