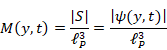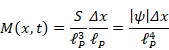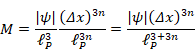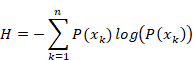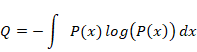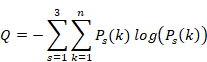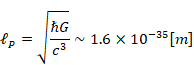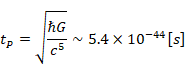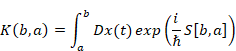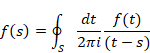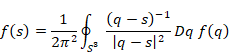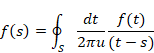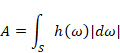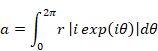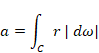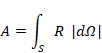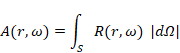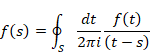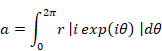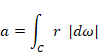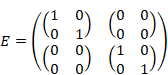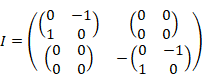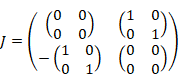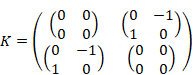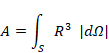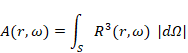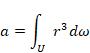多世界解釈と確率論によるボルンの規則の導出
ホーム > 量子力学 > 量子力学の確率解釈導出
2019/02/21
公開日 2012/09/26
K. Sugiyama[1]
ボルンの規則とは、電子のような小さな粒子を観測する確率が、波動関数の絶対値の2乗に比例するという規則である。本論文では、多世界解釈でボルンの規則の導出を試みる。
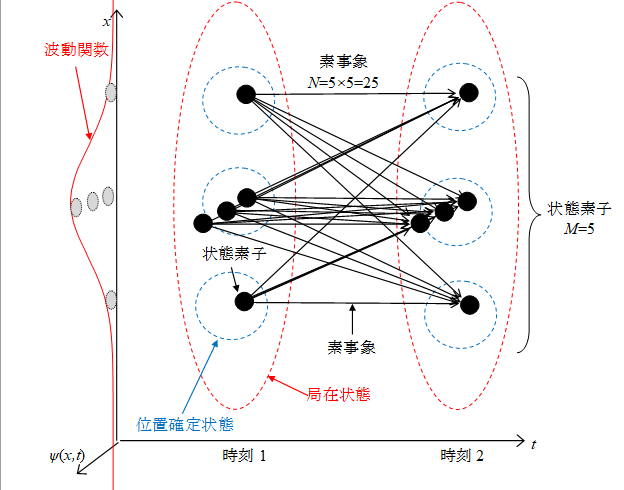
図 3-6: 経路積分の網目構造によるボルンの規則の導出
多くの研究者が多世界解釈でボルンの規則(ボルンの法則または確率解釈)の導出を試みてきた。しかし、誰も成功していない。このためボルンの規則の導出は多世界解釈の重要な課題となっていた。本論文では新しい方法として、量子論に確率論の素事象(または根元事象)を導入し、ボルンの規則導出を試みる。
波動関数の絶対値を多様体の表面積とする。その多様体の表面上の位置を素位置とする。素位置に存在する粒子を状態素子とする。状態素子が素位置に存在する状態を素状態とする。素状態から素状態への遷移を素事象とする。
確率は素事象の本数に比例し、事象素の本数は素状態の個数の二乗となる。素状態の個数は多様体の表面積に比例し、多様体の表面積は波動関数の絶対値である。したがって、確率は波動関数の絶対値の二乗に比例する。
目次
1 序論
1.1 課題
ボルンの規則によると、粒子の観測確率は波動関数の絶対値の2乗に比例する。本論文の課題は、事象の個数を数えることでボルンの規則を導出することである。
1.2 課題の重要性
波動関数の収縮とボルンの規則は量子力学の原理である。多世界解釈は、波動関数の収縮を量子力学から除いたが、ボルンの規則を除くことができなかった。このため、多くの研究者がボルンの規則の導出を試みてきた。しかし、それらの試みは成功しなかった。このため、確率を導出することが重要な課題となっていた。
1.3 これまでの導出方法
ヒュー・エヴェレット3世[2]は1957年に、多世界解釈でボルンの規則が導出できると主張した。その後も多くの研究者がエヴェレットとは異なる方法で、ボルンの規則を導出したと主張してきた。ジェームズ・ハートル[3]が1968年に、ブライス・ドウィット[4]が1970年に、ニール・グラハム[5]が1973年に主張している。しかし、それらの導出方法には不十分な点があることをエイドリアン・ケント[6]が1990年に指摘している。その後、デイヴィッド・ドイッチュ[7]が1999年にボルンの規則の導出を試みている。和田純夫氏[8]も2007年にそれを試みた。しかし、研究者の間で合意の得られたボルンの規則の導出方法は存在していない。
1.4 本論文の新しい導出方法
確率論において、我々は確率を素事象(根元事象)の概念で説明してきた。そのため、量子論の確率も同じ概念で説明できる可能性がある。そこで、本論文では新しい方法として、量子論に素事象の概念を導入しボルンの規則の導出を試みる。
2 これまでの導出方法とその問題点
2.1 ボルンの規則
マックス・ボルン[9]は1926年にボルンの規則を提唱した。それは、ボルンの法則または確率解釈とも呼ばれている。ボルンの規則は量子力学の基本原理である。量子力学では、粒子の状態は波動関数ψ(x)で表現される。波動関数の例を次の図に示す。
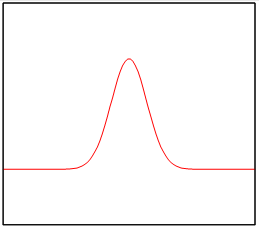
図 2-1: 波動関数の例
粒子の観測確率は波動関数の絶対値の2乗に比例する。位置 xにある粒子の観測確率 P(x) を次のように表現する。
|
|
(2.1) |
量子力学の一般的な解釈であるコペンハーゲン解釈によれば、波動関数は物理的に実在しないため、観測前の粒子の状態を記述できない。しかし波動関数は物理的に実在している可能性がある。波動関数の実在を前提とする解釈の1つが多世界解釈である。
2.2 エヴェレットの多世界解釈
エヴェレットは宇宙の波動関数を取り扱うため、1957年に多世界解釈を提唱した。彼は測度でボルンの規則の導出を試みた。
例として、シュテルン=ゲルラッハの実験を考える。我々は任意の方向のスピンの状態を、z軸についてスピン上向き状態とz軸についてスピン下向き状態の重ね合わせで表現できる。したがって、電子のスピンの状態ベクトルは、z軸についてのスピン固有ベクトルで次のように表現できる。
|
|
(2.2) |
係数a と ak は複素数である。ここで、 |ψ> と |z+>, |z−> は次のように規格化されている。
|
|
(2.3) |
|
|
(2.4) |
|
|
(2.5) |
エヴェレットは確率を導出するため測度という新しい概念を導入した。彼は測度を正の関数m(a) で表現した。彼は、この測度に対し次の等式を要求した。
|
|
(2.6) |
この要求を正当化する理由としてエヴェレットは確率保存則をあげている。この等式を満たす関数は、正の定数 c を用いて次のように書く。
|
|
(2.7) |
|
|
(2.8) |
|
|
(2.9) |
上記の式は1957年にアンドリュー・グリーソン[10]が一般的に証明している。その証明は『グリーソンの定理』と呼ばれている。エヴェレットは無限回の測定を考察し、測度が確率と同等にふるまうと結論した。しかし、エヴェレットの多世界解釈には基底問題と確率問題がある。それらについて次の節で説明する。
2.2.1 多世界解釈の基底問題
ある特定の基底で測度を定義する場合、その特定の基底を選択する方法を示す必要がある。しかし、エヴェレットは、その論文で特定の基底を選択する方法を示さなかった。
電子の波動関数をz軸のスピンの固有状態の基底で次のように表現できる。
|
|
(2.10) |
z軸のスピンの固有状態の測度は次のように表現できる。
|
|
(2.11) |
|
|
(2.12) |
一方、電子の波動関数をx軸のスピンの固有状態の基底で表現することもできる。
|
|
(2.13) |
x軸のスピンの固有状態の測度は次のように表現できる。
|
|
(2.14) |
|
|
(2.15) |
もしエヴェレットの測度が物理的に実在する量ならば、固有状態の基底の選択で変化すべきではない。なぜなら、物理的に実在する量は、その量を観測する方法に依存しないからである。したがって、我々は特定の基底を選択する方法を必要とする。しかしエヴェレットはその方法を示さなかった。
2.2.2 多世界解釈の確率問題
エヴェレットは、測度理論でボルンの規則の導出を試みた。その際、エヴェレットは測度に物理的な意味を与えなかった。しかし、測度の等式に対し確率保存則を要求することは、測度を確率と定義することと同値である。そのため無限回の測定で測度が確率として振る舞うことを示すことは循環論法となっている。
もし世界の個数が測度に比例するならば、世界の個数が測度に比例する仕組みを明らかにする必要がある。もし世界の個数が測度に比例しないならば、世界の出現確率が測度に比例する仕組みを説明する必要がある。
3 新しい導出方法
3.1 多世界解釈における素事象
本論文では多世界解釈を採用することにより量子力学に素事象を導入する。
量子論の事象を素事象の集合と解釈すれば、事象の確率を、その事象に属する素事象の個数を数えることで導出できる。ある観測で事象 R または事象 B が発生する場合、多世界解釈では、ある歴史は、事象Rが発生した歴史と、事象Bが発生した歴史に分岐する。
たとえば、事象Rの素事象の個数が3個、事象Bの素事象の個数が2個の場合、事象Rの発生確率は3/5となる。
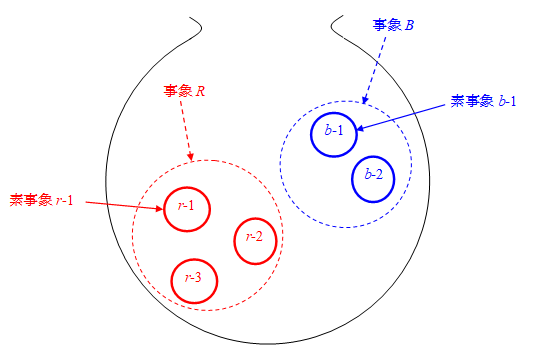
図 3-1: 多世界解釈では歴史は素歴史の集合
素事象の具体的な導入方法は次節以降で説明する。
3.2 多世界解釈における素状態
この論文では、配位空間における多粒子系の波動関数(多粒子波動関数)において、多粒子の位置が確定した状態(位置固有状態)を位置確定状態、または確定状態と呼ぶこととする。
実際の実験では、粒子は狭い範囲に広がっている。したがって、実際の状態は、配位空間内のある狭い範囲に拡散している。このような状態は確定状態の集合とみなせる。そこで、このような状態を「局在状態」と呼ぶこととする。
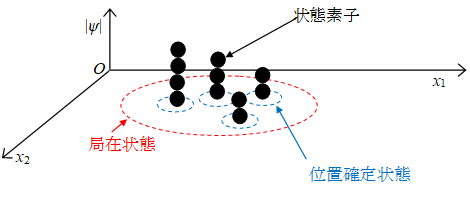
図 3-2: 多世界解釈の素状態
波動関数の絶対値を多様体の表面積とする。その多様体の表面上の位置を素位置とする。素位置に存在する粒子を状態素子とする。状態素子が素位置に存在する状態を素状態とする。
本論文の議論対象に関して言えば、1粒子の波動関数を使って、多粒子波動関数を使った議論と同じ議論をすることができる。したがって、本論文では、多粒子波動関数ではなく1粒子の波動関数で議論する。
3.3 量子論への素状態の導入
波動関数 ψ(x) をディラックのデルタ関数で次のように表現する。
|
|
(3.1) |
状態ψ(x')δ(x − x') を、その粒子の位置 x が位置x'に確定した状態すなわち「確定状態」とみなす。状態δ(x − x')を素状態とみなす。素状態はK. Sugiyama[11]が1999年に導入した。
仮想的な高次元のユークリッド空間を「素領域」で分割し、その格子点を素状態とする。確定状態を1次元球面、または3次元球面とし、その球面上の格子点をその確定状態の素状態とする。
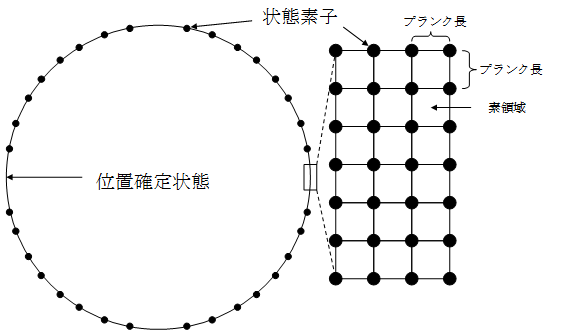
図 3-3: 多世界解釈の素状態
多様体の表面積 |S| が波動関数の絶対値 |ψ (y, t)| であるため、素状態の個数
M(y, t) は、プランク長 ![]() で次のように表現できる。
で次のように表現できる。
|
|
(3.2) |
3.4 経路積分の場への適用
場の量子論では経路積分を場に適用する。一方、状態素子は場を構成している。したがって、我々は経路積分を状態素子に適用する。
波動関数ψの高さを引数とするような新しい波動関数Ψを導入する。
|
|
(3.3) |
「位置的物理量」である位置xに対しては「経路積分の網目構造」がある。(8.5節を参照) そのため「位置的物理量」である場ψに対しても、次の図のように「経路積分の網目構造」を適用する。
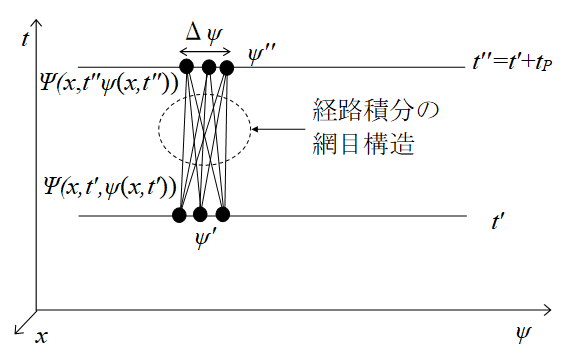
図 3-4: 経路積分の網目構造の場自体への適用
上記の図において、範囲がΔψより小さい位置ψに対して「経路積分の網目構造」を適用する。
3.5 量子論への素事象の導入
本論文では、素事象という新しい概念を量子論に導入する。
量子論では、事象は、ある状態から別の状態への遷移として表現する。そのため、素事象を、素状態から素状態への遷移として表現する。
仮に点Aから点Bへの矢印が存在すれば、逆に点Bから点Aへの矢印も存在する。点の個数がM個ならば、矢印の本数はM 2本となる。別の言い方をすれば、素状態の個数がM個であれば、素事象の本数は M 2 本となる。
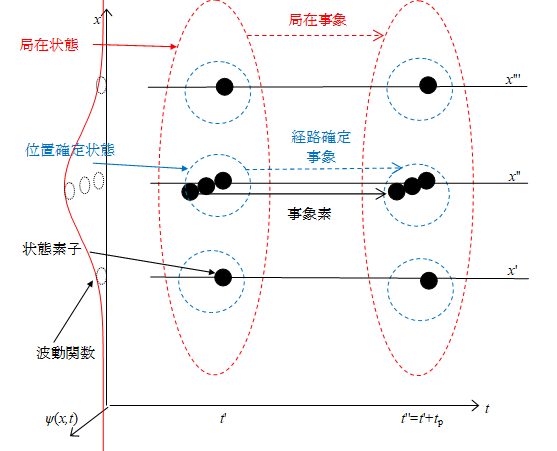
図 3-5: 多世界解釈の素状態と素事象
本論文の事象素が、確率論の素事象(または根元事象)と同じ性質を持つと仮定する。つまり、ある事象の発生確率は、その事象が含む素事象の本数に比例する。
また、確定状態から確定状態への遷移を経路確定事象または確定事象と定義する。確定事象は素事象の集合である。
実際の状態は不確定性原理により局在している。このような状態を「局在状態」と呼ぶこととする。また、局在状態から局在状態へ遷移する事象を局在事象と定義する。
離散時空に経路積分を適用すると、確定状態からの長距離遷移が発生する。しかし、局在状態により長距離遷移は抑制される。これは長距離遷移する局在事象が含む素事象が非常に少ないことを意味する。
素状態と素事象の存在は、存在確率と、発生確率が異なることを示唆する。もし、ある状態の素状態がm個ならばその状態の存在確率はmに比例する。もし、ある事象の素事象がn本ならば、その事象の発生確率はnに比例する。
3.6 ボルンの規則の導出
本節では確率の導出方法を説明する。
粒子の観測確率 P(x, t) は波動関数 ψ(x, t) で次のように表現される。
|
|
(3.4) |
一方、確率 P はラプラスの確率の計算方法に基づいて、次のように表現される。
|
|
(3.5) |
ここで Na はすべての素事象の本数であり、N は期待する素事象の本数である。Na が Nより十分大きいとすれば、確率 P は N に比例する。
|
|
(3.6) |
実際の状態は局在状態である。局在状態には「経路積分の網目構造」を適用する。局在状態では、長距離遷移は発生しないため、最小時間 tP 後の遷移距離は小さい。
局在状態 ψ (x', t') Δx にある素状態の個数 M (x', t') は、多様体の表面積に比例する。この多様体の表面上の位置に「経路積分の網目構造」が適用される。
最小時間後の多様体は、元の多様体とほとんど同じなので、同じ多様体で近似できる。多様体の表面上の素状態の個数 M (x, t) は次のとおり。
|
|
(3.7) |
したがって、Δxがほとんど一定ならば素状態の個数は波動関数の絶対値に比例する。
|
|
(3.8) |
不確定性原理により、運動量の偏差Δpがほとんど一定ならばΔxはほとんど一定である。したがって、素状態の個数Mはプランク秒tPの間ではほとんど変化しない。
|
|
(3.9) |
素事象の本数 N は時刻1 のすべての素状態とプランク秒tP後の時刻2 のすべての素状態の間の遷移の個数である。そのため、素事象の本数 N は素状態の個数 M の2乗となる。
|
|
(3.10) |
それらの素事象を次の図のように表現する。
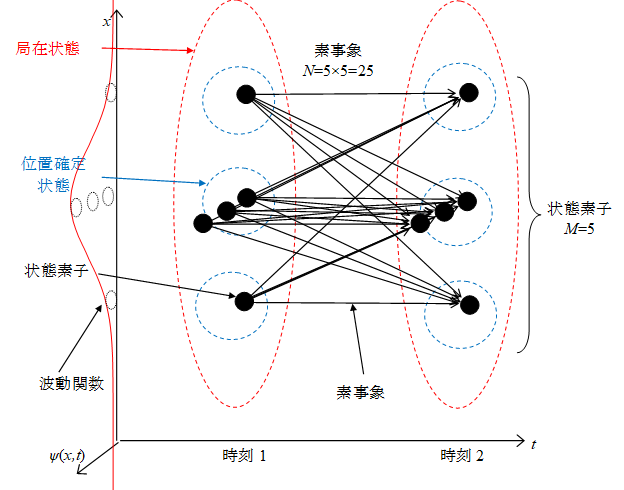
図 3-6: 経路積分の網目構造によるボルンの規則の導出
確率Pは素事象の本数Nに比例する。
|
|
(3.11) |
一方、素事象の本数Nは、素状態の個数Mの2乗と等しい。
|
|
(3.12) |
素状態の個数Mは波動関数の絶対値に比例する。
|
|
(3.13) |
そのため、確率Pは波動関数の絶対値の2乗に比例する。
|
|
(3.14) |
上記の方法により、ボルンの規則を導出した。
4 結論
多世界解釈と確率論で、ボルンの規則の導出方法を説明した。
確率は素事象の本数に比例する。素事象は素事象である。素事象の本数は素状態の個数の2乗となる。なぜならば素状態には「経路積分の網目構造」が適用されるためである。素状態の個数は波動関数の絶対値に比例する。したがって、確率は波動関数の絶対値の2乗に比例する。
5 補足
5.1 多粒子波動関数の補足
宇宙を対象とする「素状態」「確定状態」「局在状態」をそれぞれ「世界素子」「確定世界」「局在世界」と呼ぶこととする。
また、宇宙を対象とする「素事象点」「確定事象」「局在事象」をそれぞれ「素歴史」「確定歴史」「局在歴史」と呼ぶこととする。
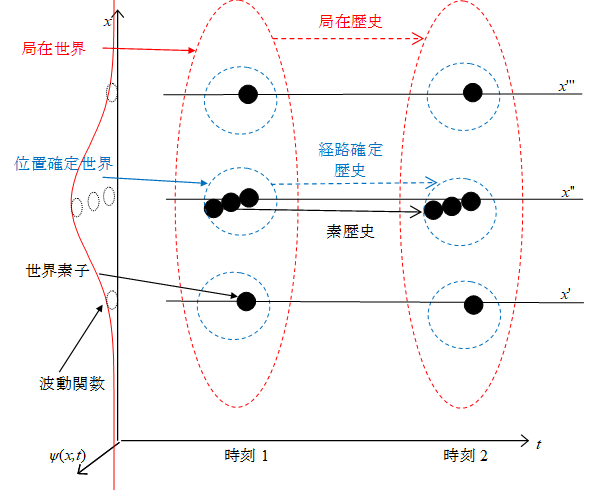
図 5-1: 多世界解釈の素歴史と世界素子
多粒子波動関数の配位空間の一点を、宇宙にあるすべての素粒子の位置が確定した状態と解釈する。そのような状態は「確定世界」である。
古典力学的観点では確定世界は私たちの世界である。量子力学的観点では局在世界が、普段私たちが生活している世界である。
宇宙の多粒子波動関数の絶対値は、ほとんどの領域でほぼゼロだと推測する。大きな絶対値を取る領域は網の目のように局在しているだろう。
5.2 ボルンの規則の導出方法の補足
多世界解釈でボルンの規則を導出する最も単純な方法は、世界の数を確率に対応させることである。
事象Aの発生確率が事象Bよりも高いならば、事象Aが発生した世界の個数は、事象Bが発生した世界の個数よりも多いと推定する。
たとえば、地球とまったく同じ100個の惑星を作るとする。80個の惑星で事象Aが発生し、20個の惑星で事象Bが発生すれば、事象Aの発生確率は80%と解釈する。
しかし、世界を数える方法が明らかでない。そこで、事象Aが発生した局在世界が含んでいる世界素子の個数を数えることとする。
局在世界の世界素子の個数Mは、事象Aが発生した波動関数ψで、次のように表現する。
|
|
(5.1) |
Δxは位置の偏差、nは全粒子の個数である。このように世界素子の個数は波動関数の絶対値に比例する。
|
|
(5.2) |
一方、確率は波動関数の絶対値の2乗に比例する。そのため、確率を世界素子の個数で説明できない。
この問題を解決するため、歴史の数で確率を説明する。事象Aが発生した局在歴史の素歴史の本数Nは次の式で計算する。
|
|
(5.3) |
確率は素歴史の数に比例する。
|
|
(5.4) |
素歴史の数は世界素子の数の2乗になる。
|
|
(5.5) |
一方、世界素子の数は波動関数の絶対値に比例する。
|
|
(5.6) |
そのため、確率は波動関数の絶対値の2乗に比例する。
|
|
(5.7) |
5.3 多世界解釈の基底問題の補足
多世界解釈において、波動関数に特定の基底が存在しないことは問題である。
たとえば、電子のスピンをシュテルン=ゲルラッハの実験で測定するケースを考える。この実験では、磁場勾配をかけてスピンを測定する。この磁場勾配の方向でスピンの基底が決まるためスピンには特定の基底が存在しない。
本論文では波動関数の特定の基底として位置を選択した。特定の基底として運動量を選ぶこともできたが、そうはしなかった。なぜなら、運動量の基底は、位置を基底とした素状態の集合で表現するためである。
スピンについては、特定の基底を選択する方法がない。そのため、スピンの基底の選択によって、測度が変わるという問題が生じる。その問題の原因は、ひとつの素状態が、スピン上向きの粒子がある状態を構成しているという解釈にある。
スピンが、3次元球面の回転で導出できることは次の論文で示した。
・3次元球面の回転によるスピン1/2の二価性と角運動量の導出 [2013/5]
スピンが3次元球面の回転ならば、多くの素状態がスピン上向きの粒子のある状態を構成していると解釈できる。スピンの基底の選択は、この3次元球面の観測軸を変えることに相当する。観測軸が、スピン上向き状態の状態に属す素状態の集合と、スピン下向き状態に属す素状態の集合を決定する。従って、多世界解釈の基底問題は三次元球面の回転で解決できる。
5.4 多世界解釈の時間の補足
多粒子波動関数の配位空間の点ごとに、すべての粒子の位置が異なる。このため、配位空間の点ごとに時刻を定義する。配位空間の点は、確定世界に対応するため、時刻は確定世界を分類するパラメータと解釈する。
配位空間内で確定世界は最小距離を連続して遷移する。われわれはその遷移を時間と感じていると推測する。
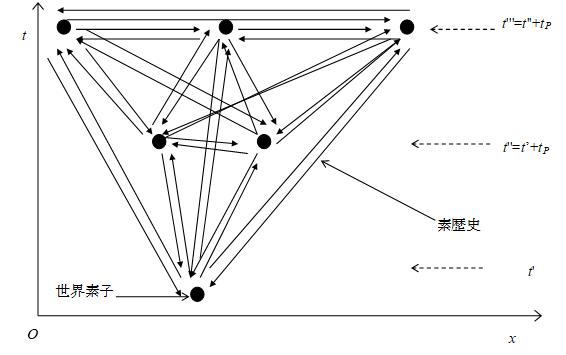
図 5-2: 多世界解釈と時間の矢
ある方向の遷移が存在すれば、その逆方向の遷移も存在する。しかし、過去の世界素子よりも未来の世界素子が圧倒的に多いため、われわれの世界素子が常に未来の世界素子に遷移しているように感じる。このように多世界解釈は、時間の矢を説明する。
5.5 長距離遷移の補足
本論文では、1カ所に局在している1個の粒子を考えてきた。ここで、ある時刻に1カ所に局在している1個の粒子の波動関数を考えよう。その波動関数が分離し、2カ所に局在したとする。このような局在状態を「多局在状態」と呼ぶこととする。この時、何が発生するだろうか?
任意の2つの素状態の間に素事象が存在する。世界が無秩序とならないのは局在状態により長距離遷移が抑止されるためである。2つの局在状態の間の局在事象の個数は、その2つの局在状態に含まれる素状態の個数だけで決定される。
したがって、二つの離れた「多局在状態」があれば、二つの局在状態の間で遷移が発生する。
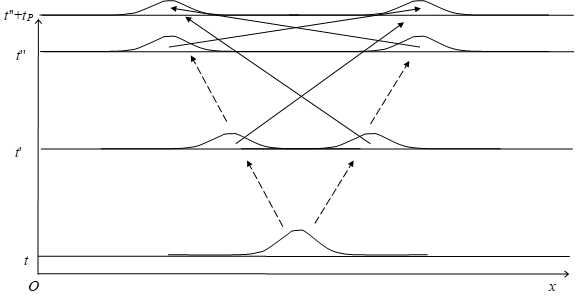
図 5-3: 局在長距離遷移
この現象を「局在長距離遷移」または「局在転移」と名づける。
では、異なる時刻の局在状態間で局在転移は発生するだろうか?
この場合においても、任意の2つの素状態の間に素事象が存在するため、局在転移が発生する。
EPR相関を利用して情報を送ることができないため、この局在転移は情報を送らないと推論する。
5.6 観測に関する補足
観測とは次に示す不確定情報量Qを確定情報量(エントロピー)Hに変換する操作である。
観測済みの情報に対して、確定情報量(エントロピー)Hを定義する。
(確定情報量)
|
|
(5.8) |
未観測の波動関数 ψ (x) に対する不確定情報量Qを次にように定義する。
(不確定情報量)
|
|
(5.9) |
|
|
(5.10) |
未観測のk番目の粒子の角運動量に対する不確定情報量Qを次にように定義する。
(不確定情報量)
|
|
(5.11) |
|
|
(5.12) |
|
|
(5.13) |
|
|
(5.14) |
そして、次の一般情報量G(単位:bit)を定義する。
(一般情報量)
|
|
(5.15) |
この一般情報量は保存する。
(一般情報量の保存則)
|
|
(5.16) |
熱力学第二法則により、確定情報量(エントロピー)は常に増大する。
(確定情報量の増大則)
|
|
(5.17) |
しかし、不確定性原理のため、確定情報量には次の上限が存在する。
(確定情報量の上限値)
|
|
(5.18) |
すべての粒子のx方向の角運動量が確定した時、y方向およびz方向の角運動量が不確定となる。
波動関数が収縮すると、確定情報量が増大する。
波動関数が拡散(反収縮)すると、不確定情報量が増大する。
ある状態を不確定状態にすると、不確定情報量が増大する。
6 今後の課題
今後の課題は次の通りである。
(1) 原理の考察
(2) 場の量子論のための定式化
(3) 離散空間の考察
(4) 相対論的力学のための定式化
(5) 重力理論のための定式化
これらの課題のうちのいくつかについて次章以降で考察する。
7 今後の課題の考察
7.1 原理の考察
階層原理と事象原理を考察する。
7.1.1 階層原理
次の階層原理を提案する。
(1) 波動関数は四元数の関数である。
(2) 粒子の閉経路と波動関数の直積が別の宇宙である。
(3) 別の宇宙の波動関数も四元数の関数である。
階層原理に基づく理論を階層論と呼ぶこととする。
7.1.2 事象原理
次の事象原理を提案する。
(1) 素事象とはある素状態から別の素状態への遷移である。
(2) ある事象の発生確率は、その事象が含む素事象の本数に比例する。
事象原理に基づく理論を事象論と呼ぶこととする。
7.2 場の量子論のための定式化の考察
確定状態は、波動関数の位相と絶対値を持つ。そのため、確定状態に対して、「局在状態による長距離遷移の抑止」の論理が使える。一方、素状態は、波動関数の位相と絶対値を持たない。そのため、素状態に対しては、「局在状態による長距離遷移の抑止」の論理が使えない。この問題を解決するため、場の量子論について考察する。
量子力学では、粒子の位置と運動量が交換関係を持つ。これは粒子の位置が広がっていることを意味する。一方、場の量子論では、波動関数の振幅と一般運動量が交換関係を持つ。これは波動関数の振幅が広がっていることを意味する。
そこで次の新しい関数を提案する。
|
|
(7.1) |
場の第二量子化で得た波動関数であるため、この関数を第二波動関数と呼ぶ。第二波動関数は第二宇宙に存在する。第一宇宙の素状態は、第二宇宙の確定状態である。従って「局在状態による長距離遷移の抑止」を素状態に使うことができる。
8 付録: これまでの考え方の確認
8.1 ホイーラーとデウィットの宇宙波動関数
ジョン・ホイーラーとブライス・デウィット[12]は、1967年に宇宙波動関数を提唱した。その波動関数はハミルトニアン演算子 H とケットベクトル |ψ> を用いて次のように表現される。
|
|
(8.1) |
このケットベクトル |ψ> は通常の関数ではなく汎関数である。
汎関数は数学的には多変数関数とほとんど同等である。汎関数での議論は難しいため、本論文では多変数関数で議論する。次の節で、多変数関数である多粒子波動関数について説明する。
8.2 バーバーの宇宙の多粒子波動関数
ジュリアン・バーバー[13]は1999年に著書『時間の終焉』で宇宙を多粒子系の波動関数(多粒子波動関数)で表現した。
宇宙に素粒子がn個あり、k番目の素粒子の位置を
rk = (xk, yk, zk ) とする。このとき、多粒子波動関数ψは次のように表現される。
|
|
(8.2) |
多粒子の位置を表現した多次元空間を配位空間と呼ぶ。
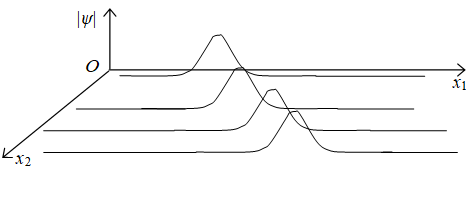
図 8-1: 多粒子波動関数
配位空間の一点は、すべての粒子の位置を表現するため、配位空間は過去、現在、未来の物理的に可能なすべての世界を表現する。別の言い方をすれば、多粒子波動関数は、多世界解釈におけるすべての可能な世界を表現する。
ある世界のすべての粒子の配置が決まれば、その世界の時計の状態が決まる。その世界の時計の状態が決まれば、その世界の時計の時刻が決まる。そのため、多粒子波動関数の引数に時刻は不要となる。
波動関数の基底として位置または運動量を選択できる。本論文は位置を基本的な基底として選択する。なぜなら、常に我々は実験で最終的に位置を観測するからである。
場の量子論では粒子数が変化する。このため多粒子波動関数は量子場を表現できない。量子場を表現するため、我々は汎関数を必要とする。一方、汎関数は多変数関数で近似的に表現できる。そこで、簡単に議論するため、本論文では、多変数関数である多粒子波動関数を使用する。
配位空間内で、それぞれの世界を観測する確率 P を次の式で表現する。
|
|
(8.3) |
確率がこの式で表現される理由を考察するため、次節では確率論の考え方を確認する。
8.3 ラプラスの確率論
ピエール=シモン・ラプラス[14]は1814年に古典的確率論をまとめた。彼は次のような、確率の計算方法を示した。
任意の一つの場合が他の場合よりも頻繁に起きると推論させる事実が存在しない時、すなわち、任意の一つの場合が同様に確からしい時、期待する事象の確率は、期待する事象に都合のよい場合の個数と、可能なすべての場合の個数の比となる。
この「同様に確からしい」場合が、確率論における素事象である。すべての素事象の発生確率は等しい。
素事象は根元事象とも呼ばれる。本論文では「同様に確からしい」場合を素事象と呼ぶ。
すべての素事象の個数を Na とし、ある事象の素事象の個数を N とする。このとき、その事象の発生確率 P は次の式で表現される。
|
|
(8.4) |
|
|
(8.5) |
たとえば、袋に5個の玉が入っているとする。5個のうち3個を赤玉、2個を青玉とする。赤い玉を取り出す事象の確率をPとする。このとき、確率Pは3/5となる。
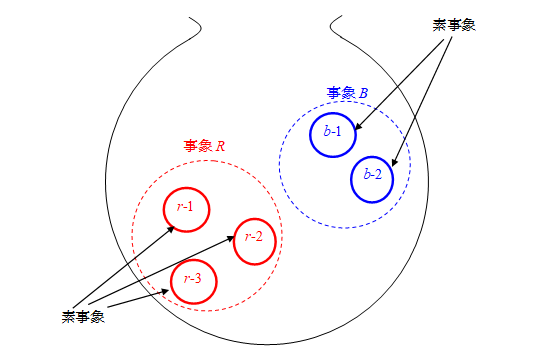
図 8-2: 事象は素事象の集合
この理由は素事象の概念を用いて説明される。確率論では、個々の玉を取り出す事象が素事象である。事象は素事象の集合と解釈する。
ボルンの規則を導出するためには、量子論における素事象を発見する必要がある。確率論の素事象は一般に、それ以上分けることができないため、量子論の素事象もそれ以上分けることができないことが期待される。
8.4 ペンローズのスピンネットワーク
ロジャー・ペンローズ[15]は1971年にスピンネットワークを提唱した。スピンネットワークでは、時空は離散的であり、空間は点と点を線で結んだグラフで表現される。このグラフはスピンネットワークと呼ばれる。時空が離散的であるため、時空は最小距離と最小時間を持つ。
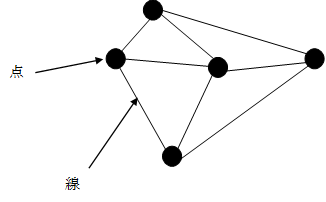
図 8-3: ペンローズのスピンネットワーク
本論文は、スピンネットワークは利用しないが、この理論と同様に時空が離散的すなわち不連続であることと、空間が点と点を線で結んだグラフであることを仮定する。本論文では、最小距離をプランク長
![]() と仮定する。また最小時間をプランク時間
tP と仮定する。
と仮定する。また最小時間をプランク時間
tP と仮定する。
|
|
(8.6) |
|
|
(8.7) |
プランク長で構成した最小の領域を素領域と呼ぶこととする。
時空が不連続であれば、連続な時空を前提に構築していた理論を再検討する必要がある。そこで、次節では、経路積分が不連続な時空でどうなるかについて再検討する。
8.5 ファインマンの経路積分
リチャード・ファインマン[16]は1948年に経路積分を提唱した。経路積分は新しい量子化方法を提供する。経路積分では、粒子が取りうるすべての経路の和を取る。
位置aから位置bへの確率振幅K(b, a)は次のように表現される。
|
|
(8.8) |
確率振幅K(b, a)は伝播関数(プロパゲータ)と呼ばれている。記号Dx(t) はすべての経路に対する確率振幅の和を表現している。波動関数は伝播関数で次のように表現される。
|
|
(8.9) |
経路積分では粒子が位置 a から位置 b に移動する事象を伝播関数 K(b, a) に対応させている。時刻taの波動関数に伝播関数 K(b, a) を乗じ積分することで、時刻 tb の波動関数を求める。
経路積分では、次の図に示すように、普通の経路 α のようなものだけでなく、短時間に長距離を移動する経路 β も存在する。このような経路は、光速を超えることもある。そのためこのような経路は、特殊相対性理論に反するため許されない。このような経路の移動を本論文では長距離遷移と呼ぶこととする。
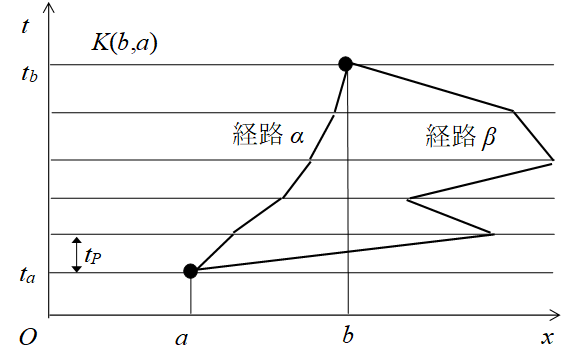
図 8-4: ファインマンの経路積分
一般に経路積分の教科書では、次のように説明している。経路 α に近い微小に異なる経路の和は大きくなる。一方、経路 β に近い微小に異なる経路の和は小さくなる。このため、長距離遷移は抑制され、経路 β は残らない。
それでは、最小時間 tP 後の場合には、何が起こるだろうか?位置 a から位置 b までの最小時間 tP 後の伝播関数 K(b, a)は次のように表現する。
|
|
(8.10) |
本論文では時間の不連続性を仮定している。最小時間は、それ以上分割できないため、出発地点と到着地点が決まっている場合には微小に異なる経路を取ることができない。このため、長距離遷移は抑制されず、経路βは残る。
したがって、もし、離散時空に経路積分を適用し、粒子の位置がディラックのデルタ関数のように決定されていたら、最小時間tP秒後に長距離遷移が生じる。
|
|
(8.11) |
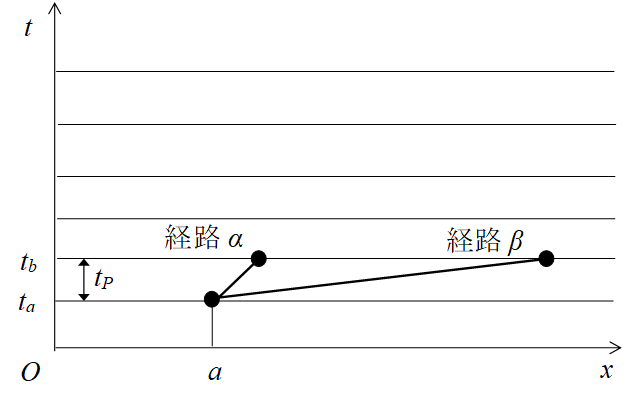
図 8-5: 経路積分における長距離遷移
しかし、実際に長距離遷移を観測することはない。この理由は、粒子の位置が次の図のように正規分布で分布しているためであると推論する。
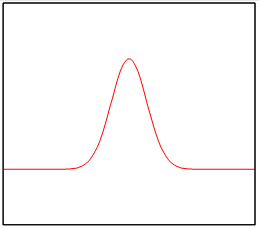
図 8-6: 局在状態の波動関数
そのため、位置xは、偏差Δxで分布し、運動量pも偏差Δpで分布する。不確定性原理によりΔxとΔpの積はプランク定数
![]() に近い。
に近い。
|
|
(8.12) |
正規分布している波動関数の状態を本論文では局在状態と呼ぶこととする。
運動量pを持つ粒子の波動関数は次のように表現できる。
|
|
(8.13) |
この粒子の質量をm、速度をvとする。その運動量は次のとおり。
|
|
(8.14) |
この式を波動関数に代入すると次の式を得る。
|
|
(8.15) |
速度vは、移動距離xとプランク時間tPで次のように表現できる。
|
|
(8.16) |
この式を波動関数に代入すると次の式を得る。
|
|
(8.17) |
上記の式より、短距離において波動関数の波長は長い。一方、長距離において波動関数の波長は短い。
そのため、短距離では、局在状態の経路積分の和は大きくなる。一方、長距離では、局在状態の経路積分の和は小さくなる。このような現象を本論文では「局在状態による長距離遷移の抑止」と呼ぶこととする。
局在状態では、最小時間tP秒後に長距離遷移は発生しない。そのため、局在状態は、tP秒後も近くに局在している。このため、次の図のような経路積分の網目構造が実現していると推論する。
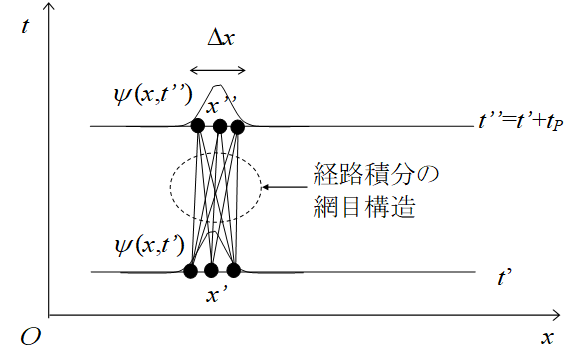
図 8-7: 経路積分の網目構造
本論文では、この経路の網目構造を、「経路積分の網目構造」と呼ぶこととする。
状態Aから状態Bへ遷移する事象ABがあるとする。状態Aに位置が3個あり、状態Bに位置が3個あれば、事象ABには経路が3 × 3 = 9本ある。
「経路積分の網目構造」では経路の本数は位置の個数の2乗となる。一方、ボルンの規則によれば、確率は波動関数の絶対値の2乗となる。本論文では、これらの2乗の類似性を議論する。
8.6 ディラックの場の量子論
ポール・ディラック[17]は、電磁波の放射と吸収を説明するため、1927年に場の量子論を提唱した。1次元の場合、場の量子論の基本交換関係[18]は次のように表現される。
|
|
(8.18) |
ここでψは場であり、 π は場 ψ の共役な演算子である。変数 x, y は位置、関数 δ はディラックのデルタ関数である。
この交換関係は、次の位置 x と運動量 p の交換関係と似ている。
|
|
(8.19) |
このことは、場ψが位置xと同様に位置的な性質を持つ物理量であることを示唆する。このような物理量を本論文では「位置的物理量」と呼ぶこととする。
位置 x に対する第一量子化によって場 ψ(x) を得た。一方、場ψは位置xのような「位置的物理量」である。このため、場 ψ(x) に対する第二量子化によって新しい場 Ψ(x, ψ(x)) を得る。この場Ψ(x, ψ(x)) を「第二波動関数」と呼ぶこととする。第二波動関数Ψ(x, ψ(x)) は次の図のように表現される。
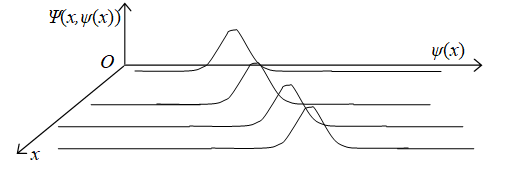
図 8-8: 第二波動関数
第二波動関数Ψ(x, ψ(x))は、汎関数Φ[ψ(x)] と解釈できる。汎関数Φ[ψ(x)]は多粒子波動関数 ψ (x1, x2, x3, …, xn) で近似できる。簡単に議論するため、本論文では多粒子波動関数を使用する。
8.7 カルツァ=クライン理論
テオドール・カルツァ[19]は1921年に、オスカル・クライン[20]は1926年に、重力と電磁気力を統一するため、1次元の円のような余剰空間を提唱した。この理論は、カルツァ=クライン理論と呼ばれている。
通常の4次元時空M4と1次元の円状の余剰空間S1で、新しい時空M4×S1を次のように表現する。
|
|
(8.20) |
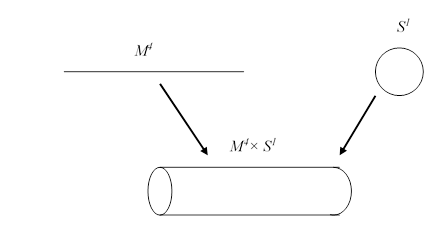
図 8-9: カルツァ=クライン理論
9 付録: これまでの考え方の確認(その2)
9.1 オイラーの公式
オイラーは1748年に次の公式を発表した。
(オイラーの公式)
|
|
(9.1) |
虚数iは次の式を満たす。
|
|
(9.2) |
複素数を次のように表現する。
|
|
(9.3) |
|
|
(9.4) |
複素共役を次のように表現する。
|
|
(9.5) |
複素関数を次のように表現する。
|
|
(9.6) |
複素数の絶対値の二乗は次のように表現できる。
|
|
(9.7) |
本論文では、次の記号を用いる。
|
|
(9.8) |
|
|
(9.9) |
9.2 コーシー=リーマンの方程式
オーギュスタン=ルイ・コーシー[21]は1814年に複素解析のため次の方程式を導入した。1851年にリーマン[22]も複素解析のために、この方程式を利用した。
(コーシー=リーマンの方程式)
|
|
(9.10) |
上記の公式を次のように短く表現する。
(コーシー=リーマンの方程式)
|
|
(9.11) |
コーシーは、次の公式を導入した。
(コーシーの積分公式)
|
|
(9.12) |
S は周回経路である。
9.3 ハミルトンの四元数
ウィリアム・ローワン・ハミルトン[23]は、1843年に四元数を発表した。
|
|
(9.13) |
四元数を次のように表現する。
|
|
(9.14) |
|
|
(9.15) |
四元数共役を次のように表現する。
|
|
(9.16) |
四元数関数を次のように表現する。
|
|
(9.17) |
四元数の絶対値の二乗を次のように表現する。
|
|
(9.18) |
本論文では次の記号を用いる。
|
|
(9.19) |
|
|
(9.20) |
9.4 コーシー=リーマン=フューターの方程式
フューター[24]は1934年に、四元数解析のため次の方程式を導入した。
(コーシー=リーマン=フューターの方程式)
|
|
(9.21) |
上記の公式を次のように短く表現する。
(コーシー=リーマン=フューターの方程式)
|
|
(9.22) |
|
|
(9.23) |
フューターは、次の公式を導入した。
(コーシー=フューターの積分公式)
|
|
(9.24) |
ここで、S3 は3次元閉曲面である。四元数解析の詳細は、1979年のアンソニー・サドベリーの論文[25]に記載されている。
本論文は、次の公式を使用する。
(四元数の積分公式)
|
|
(9.25) |
ここで、uは単位四元数である。
四元数の積分公式についての詳細は次の論文を参照。
・四元数解析によるゼータ関数の反射積分方程式の導出 [2014/5/18]
https://xseek-qm.net/Quaternion.htm
9.5 カルタンの微分形式
エリ・カルタン[26]は、座標に依存しない方法で多様体を記述するため、1899年に微分形式を定義した。
微分形式 dω は無限小だが、本論文は有限小の差分形式 δω を用いる。
多様体 S の表面積 A を次のように表現する。
|
|
(9.26) |
多様体 S の差分形式 δS を次のように表現する。
|
|
(9.27) |
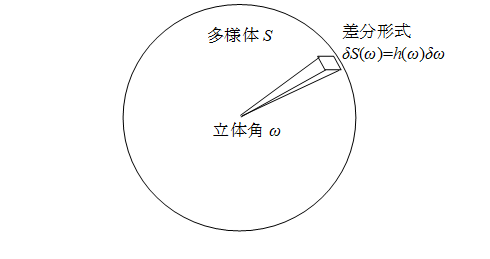
図 9-1: 多様体
ここで、多様体S1の差分形式δS1を次のように表現する。
|
|
(9.28) |
また、別の多様体S2の差分形式δS2を次のように表現する。
|
|
(9.29) |
多様体S1とS2の重ね合わせとして多様体Sを得る。
|
|
(9.30) |
波動関数の重ねあわせでは、位置ごとに波動関数の複素数を加算している。そのため、多様体の重ねあわせでは、立体角ごとに表面積を加算すると推測する。
そこで、多様体Sの差分形式δSを次のように表現する。
|
|
(9.31) |
したがって、球面調和関数に対し次の式が成立する。
|
|
(9.32) |
上記の式で多様体の重ねあわせを定義する。
10 付録: 階層宇宙
10.1 2次元時空の宇宙
10.1.1 2次元時空の閉じた経路
2次元時空の宇宙 U を考える。
粒子の世界線 s を複素数で、次のように表現する。
|
|
(10.1) |
|
|
(10.2) |
この粒子の波動関数を次のように表現する。
|
|
(10.3) |
この粒子が対生成し対消滅したとする。
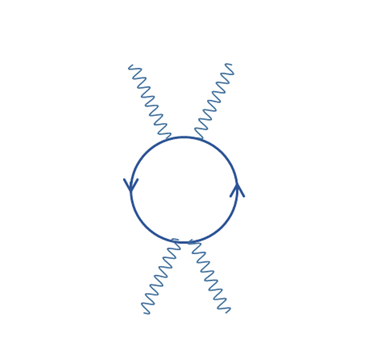
図 10-1: 対生成と対消滅
この閉じた経路sを半径rの円Cで次のように表現する。
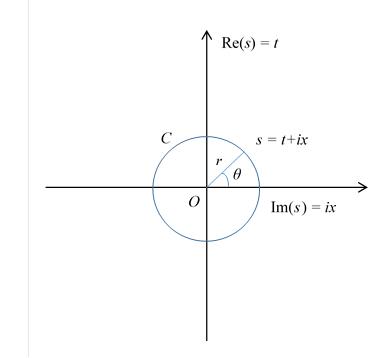
図 10-2: 閉経路C
この閉経路Cは次のように表現できる。
|
|
(10.4) |
この閉経路Cの周長 a は次のように表現できる。
|
|
(10.5) |
ここで複素立体角 ω を導入する。
|
|
(10.6) |
|
|
(10.7) |
閉経路Cは次のように表現できる。
|
|
(10.8) |
すると、周長aは次のように表現できる。
|
|
(10.9) |
周長aの差分形式を次のように表現する。
|
|
(10.10) |
10.1.2 波動関数の絶対値の導入
カルツァ=クライン理論と同様に余剰空間として円Sを導入する。
円S上の点を複素数の行列表現で次のように表現する。
|
|
(10.11) |
|
|
(10.12) |
|
|
(10.13) |
|
|
(10.14) |
この円を振幅円、または振幅1次元球面と呼ぶ。
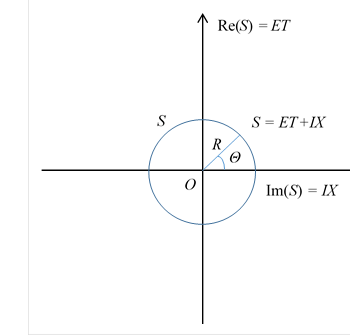
図 10-3: 振幅1次元球面S
振幅1次元球面Sの周長 A は半径Rと複素立体角 Ω で次のように表現できる。
|
|
(10.15) |
半径Rがrとω の関数ならば、周長 A もrと ω の関数となる。
|
|
(10.16) |
球面Sの差分形式δSで次のように表現する。
|
|
(10.17) |
周長 A を波動関数の絶対値と解釈する。
|
|
(10.18) |
10.1.3 波動関数の位相の導入
波動関数の位相を導入するため、この球面を回転角度 Φ で回転する。ω に依存する回転変換 P で球面 S を球面 S’ に変換する。
|
|
(10.19) |
ω に依存する回転角度 Φ の回転変換を次のように定義する。
|
|
(10.20) |
関数 Φ (ω)を自然数nで次のように表現する。
|
|
(10.21) |
この回転角度 Φ を波動関数の位相と解釈する。
|
|
(10.22) |
回転変換で球面Sの差分形式を次のように変換する。
|
|
(10.23) |
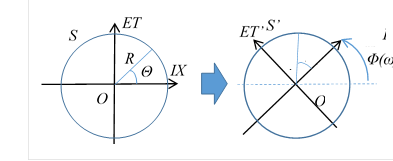
図 10-4: 振幅1次元球面Sの回転
球面S1と球面S2の重ね合わせを次のように定義する。
|
|
(10.24) |
球面と、180度回転した球面の重ね合わせは0になる。
|
|
(10.25) |
|
|
(10.26) |
粒子の閉経路Cと球面Sの直積は円環(トーラス) Tとなる。
|
|
(10.27) |
|
|
(10.28) |
|
|
(10.29) |
この円環Tを円環世界面と呼ぶ。
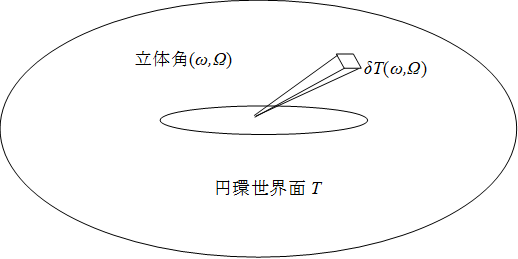
図 10-5: 円環世界面
ここで、次の新しい立体角νを導入する。
|
|
(10.30) |
ここで、次の新しい半径ρを導入する。
|
|
(10.31) |
ここで、次の新しい関数f (ρ, ν) を導入する。
|
|
(10.32) |
この関数 f (ρ, ν) を使って、円環世界面Tを次のように表現する。
|
|
(10.33) |
次の図のように、円環世界面は螺旋円環(らせんえんかん)のようにねじれている。
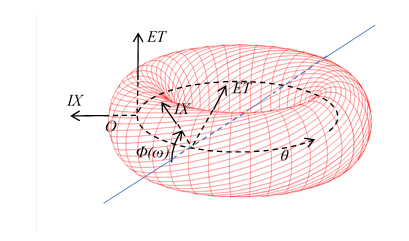
図 10-6: 円環世界面は螺旋円環のようにねじれている。
この円環世界面の次元は、宇宙の次元と同じである。なぜなら、本節の宇宙は2次元時空だからである。
ここで驚くべきアイデアを使う。
この円環世界面を新しい時空と解釈する。これを円環時空と呼ぶ。この円環時空を一つの独立した宇宙とみなす。その宇宙を第二宇宙と呼称する。
第二宇宙に、本節と同様の議論を適用することで、第三、第四の宇宙を構成できる。同じ方法を繰り返すことで多くの宇宙を構成できる。これらの宇宙を階層宇宙と呼ぶ。
10.1.4 階層宇宙
階層宇宙の図を次に示す。
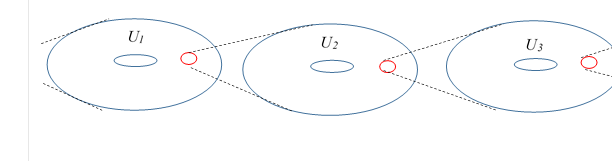
図 10-7: 階層宇宙
上記の階層宇宙を次の記号で表現する。
|
|
(10.34) |
10.1.5 方程式
位置sを複素数で次のように表現する。
|
|
(10.35) |
すると波動関数は複素関数となる。
|
|
(10.36) |
この複素関数を解析関数と仮定する。
解析関数はコーシー=リーマンの方程式を満たす。
(コーシー=リーマンの方程式)
|
|
(10.37) |
この方程式を経路微分方程式と呼ぶ。
共役を次のように定義する。
|
|
(10.38) |
すると、経路微分方程式は次のように短く書ける。
|
|
(10.39) |
解析関数はコーシーの積分公式を満たす。
(コーシーの積分公式)
|
|
(10.40) |
S は周回経路である。
コーシーの積分公式を、ファインマン経路積分の経路積分方程式と解釈する。
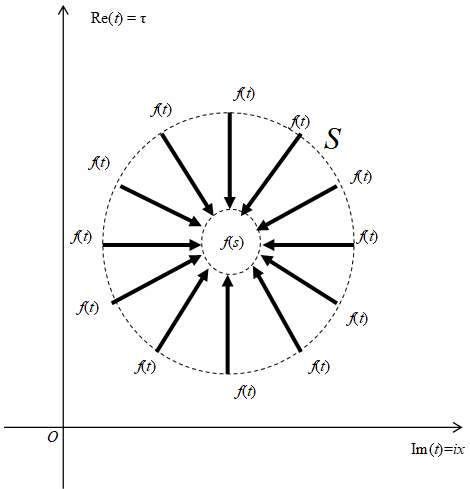
図 10-8: ファインマン経路積分の経路積分方程式
円S上の粒子が、位置tから位置sまで直接、長距離遷移すると解釈する。
従来のファインマンの経路積分と異なるこの新しい解釈を時空視点経路積分と呼ぶこととする。
各宇宙の波動関数は複素関数である。したがって、これらの方程式は、各宇宙の波動関数に適用できる。
10.2 4次元時空の宇宙
10.2.1 4次元時空の閉じた経路
4次元時空の宇宙 U を考える。
粒子の世界線を四元数sで、次のように表現する。
|
|
(10.41) |
|
|
(10.42) |
この粒子の波動関数を次のように表現する。
|
|
(10.43) |
この粒子が対生成し対消滅したとする。
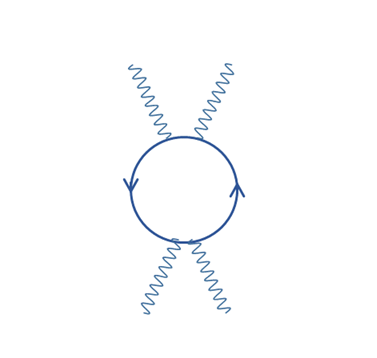
図 10-9: 対生成と対消滅
この閉じた経路sを半径rの円Cで次のように表現する。
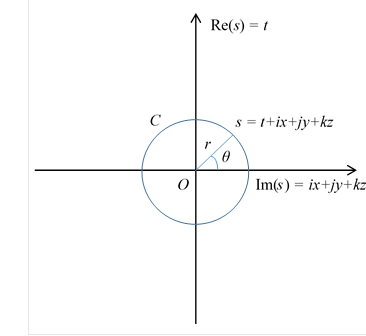
図 10-10: 閉経路C
この閉経路Cは次のように表現できる。
|
|
(10.44) |
この閉経路Cの周長aは次のように表現できる。
|
|
(10.45) |
ここで四元数立体角 ω を導入する。
|
|
(10.46) |
|
|
(10.47) |
閉経路Cは次のように表現できる。
|
|
(10.48) |
すると、周長aは次のように表現できる。
|
|
(10.49) |
周長aの差分形式で次のように表現する。
|
|
(10.50) |
10.2.2 波動関数の絶対値の導入
カルツァ=クライン理論と同様に余剰空間として3次元球面Sを導入する。
3次元球面上の点Sを四元数の行列表現で、次のように表現する。
|
|
(10.51) |
|
|
(10.52) |
|
|
(10.53) |
|
|
(10.54) |
|
|
(10.55) |
|
|
(10.56) |
この球面を振幅3次元球面と呼ぶ。
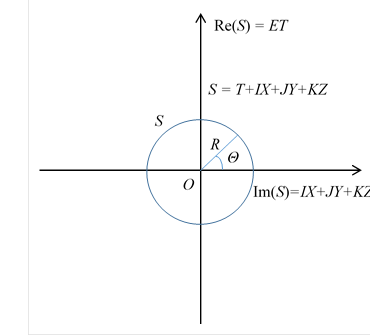
図 10-11: 振幅3次元球面S
この振幅3次元球面Sの表面積Aは半径Rと立体角Ω で次のように表現できる。
|
|
(10.57) |
半径Rがrとω の関数ならば、周長Aもrとω の関数となる。
|
|
(10.58) |
球面Sを差分形式δSで次のように表現する。
|
|
(10.59) |
周長Aを波動関数の絶対値と解釈する。
|
|
(10.60) |
10.2.3 波動関数の位相の導入
波動関数の位相を導入するため、この球面を回転角度 Φ で回転する。ω に依存する回転変換 P で球面 S を球面 S’ に変換する。
|
|
(10.61) |
ω に依存する回転角度Φの回転変換を次のように定義する。
|
|
(10.62) |
関数Φ(ω )を自然数nで次のように表現する。
|
|
(10.63) |
この回転角度Φを波動関数の位相と解釈する。
|
|
(10.64) |
回転変換で球面Sの差分形式を次のように変換する。
|
|
(10.65) |
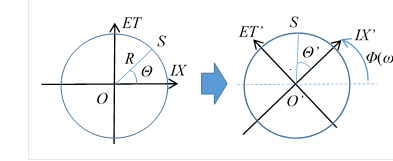
図 10-12: 振幅3次元球面Sの回転
球面S1と球面S2の重ね合わせを次のように定義する。
|
|
(10.66) |
球面と、180度回転した球面の重ね合わせは0になる。
|
|
(10.67) |
|
|
(10.68) |
粒子の閉経路Cと球面Sの直積は円環(トーラス)のような多様体 Tとなる。
|
|
(10.69) |
|
|
(10.70) |
|
|
(10.71) |
この多様体Tを円環世界面と呼ぶ。
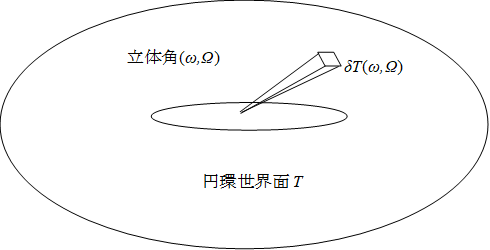
図 10-13: 円環世界面
ここで、次の新しい立体角νを導入する。
|
|
(10.72) |
ここで、次の新しい半径ρを導入する。
|
|
(10.73) |
ここで、次の新しい関数f (ρ, ν)を導入する。
|
|
(10.74) |
この関数 f (ρ, ν) を使って、円環Tを次のように表現する。
|
|
(10.75) |
次の図のように、円環世界面は螺旋円環のようにねじれている。
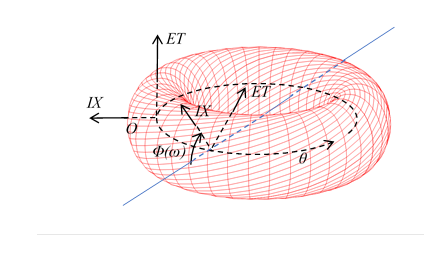
図 10-14: 円環世界面は螺旋円環のようにねじれている。
この円環世界面の次元は、宇宙の次元と同じである。なぜなら、本節の宇宙は4次元時空だからである。
ここで驚くべきアイデアを使う。
この円環世界面を新しい時空と解釈する。これを円環時空と呼ぶ。この円環時空を一つの独立した宇宙とみなす。その宇宙を第二宇宙と呼称する。
第二宇宙に、本節と同様の議論を適用することで、第三、第四の宇宙を構成できる。同じ方法を繰り返すことで多くの宇宙を構成できる。これらの宇宙を階層宇宙と呼ぶ。
10.2.4 階層宇宙
階層宇宙の図を次に示す。
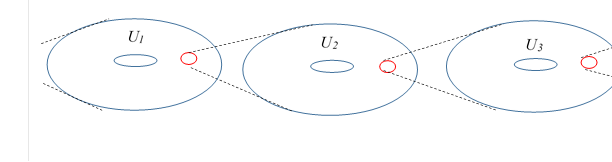
図 10-15: 階層宇宙
上記の階層宇宙を次の記号で表現する。
|
|
(10.76) |
10.2.5 方程式
位置sを四元数で次のように表現する。
|
|
(10.77) |
すると波動関数は四元数関数となる。
|
|
(10.78) |
この四元数関数を解析関数と仮定する。
解析関数はコーシー=リーマン=フューターの方程式を満たす。
(コーシー=リーマン=フューターの方程式)
|
|
(10.79) |
以下、経路微分方程式と呼称する。
共役を次のように定義する。
|
|
(10.80) |
すると、上記の式は次のように短く書ける。
|
|
(10.81) |
解析関数は次の積分公式を満たす。
(四元数の積分公式)
|
|
(10.82) |
ここで、u は単位四元数である。
四元数の積分公式は、ファインマンの経路積分の経路積分方程式と解釈できる。
その解釈を次の図に示す。
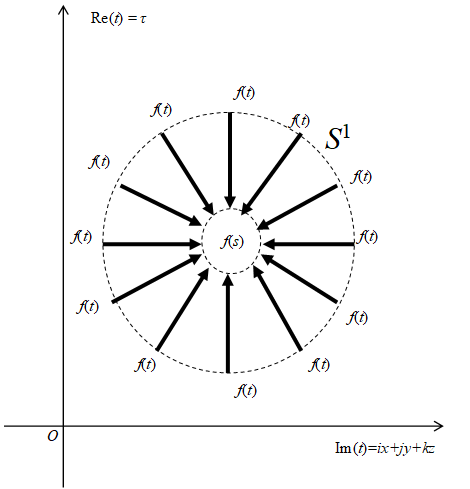
図 10-16: ファインマンの経路積分と経路積分方程式
円S1上の粒子が、位置tから位置sまで直接、長距離遷移すると解釈する。
従来のファインマンの経路積分と異なるこの新しい解釈を時空視点経路積分と呼ぶこととする。
各宇宙の波動関数は四元数関数である。したがって、これらの方程式は、各宇宙の波動関数に適用できる。
10.3 通常空間
通常時空Uの表面積aは次のとおり。
|
|
(10.83) |
通常時空Uの差分形式は次のとおり。
|
|
(10.84) |
ここで、r3を関数 f (ω) に置き換える。
|
|
(10.85) |
すると次のように書ける。
|
|
(10.86) |
この式は次の図のように解釈できる。これを多様体視点と呼ぶ。
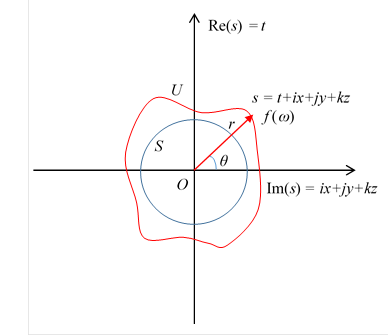
図 10-17: 通常空間Uの多様体視点
ここで式を新しい関数 f (r, ω ) で次のように書き換える。
|
|
(10.87) |
この式は次の図のように解釈できる。
これを球面調和関数視点と呼ぶ。
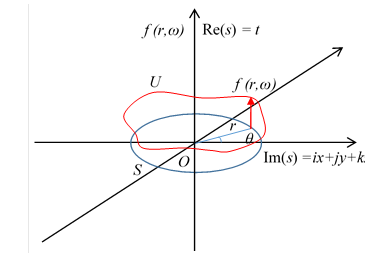
図 10-18: 通常空間Uの球面調和関数視点
球面調和関数視点では、関数 f (r,ω) を球面調和関数とみなすことができる。
球面調和関数 f (r,ω) は球座標のラプラス方程式の解である。
したがって、球面調和関数 f (r,ω) は次のラプラス方程式を満たす。
|
|
(10.88) |
ここで次の記号を用いた。
|
|
(10.89) |
|
|
(10.90) |
10.4 波動時空
通常時空Uを、半径rと立体角ω で次のように表現する。
|
|
(10.91) |
振幅3次元球面Sを、半径Rと立体角Ω で、次のように表現する。
|
|
(10.92) |
通常空間Uと振幅3次元球面Sの直積空間である波動時空Wを次のように定義する。
|
|
(10.93) |
|
|
(10.94) |
ここで、新しい立体角を導入する。
|
|
(10.95) |
ここで、新しい半径を導入する。
|
|
(10.96) |
ここで新しい関数を導入する。
|
|
(10.97) |
すると波動時空は次のように書ける。
|
|
(10.98) |
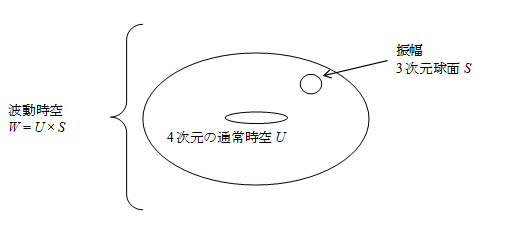
図 10-19: 波動時空
球面調和関数 g(ρ, ν) は球座標のラプラス方程式の解である。したがって、球面調和関数 g(ρ, ν) は次のラプラス方程式を満たす。
|
|
(10.99) |
ここで次の記号を用いた。
|
|
(10.100) |
|
|
(10.101) |
|
|
(10.102) |
|
|
(10.103) |
11 付録: 用語
11.1 用語定義
用語を次の表のように定義する。
表 11-1: 通常空間と波動空間
|
用語 |
定義 |
|
通常空間 |
通常の3次元空間 |
|
波動空間 |
波動関数の絶対値を表面積とする球面 |
表 11-2: 素状態など
|
分類 |
用語 |
定義 |
|
確定 |
確定位置 |
通常空間の位置 |
|
確定 |
確定状態 |
一粒子が確定位置に存在する状態 |
|
確定 |
確定世界 |
全粒子が確定位置に存在する状態 |
|
確定 |
確定状態粒子 |
確定状態にある一粒子 |
|
確定 |
確定世界粒子 |
確定状態にある全粒子 |
|
確定 |
確定経路 |
確定位置から確定位置への経路 |
|
確定 |
確定事象 |
確定状態から確定状態への遷移 |
|
確定 |
確定歴史 |
確定世界から確定世界への遷移 |
|
素 |
素位置 |
通常空間と波動空間の直積空間の位置 |
|
素 |
素状態 |
一粒子が素位置に存在する状態 |
|
素 |
素世界 |
全粒子が素位置に存在する状態 |
|
素 |
素状態粒子 |
素状態にある一粒子 |
|
素 |
素世界粒子 |
素状態にある全粒子 |
|
素 |
素経路 |
素位置から素位置への経路 |
|
素 |
素事象 |
素状態から素状態への遷移 |
|
素 |
素歴史 |
素世界から素世界への遷移 |
|
局在 |
局在位置 |
正規分布した確定位置 |
|
局在 |
局在状態 |
一粒子が局在位置に存在する状態 |
|
局在 |
局在世界 |
全粒子が局在位置に存在する状態 |
|
局在 |
局在状態粒子 |
局在状態にある一粒子 |
|
局在 |
局在世界粒子 |
局在状態にある全粒子 |
|
局在 |
局在経路 |
局在位置から局在位置への経路 |
|
局在 |
局在事象 |
局在状態から局在状態への遷移 |
|
局在 |
局在歴史 |
局在世界から局在世界への遷移 |
素状態粒子は、状態素子と略す。
素世界粒子は、世界素子と略す。
11.2 用語整理
表 11-3: 用語整理
|
分類 |
確定 |
素 |
局在 |
|
位置 |
確定位置 |
素位置 |
局在位置 |
|
状態 |
確定状態 |
素状態 |
局在状態 |
|
世界 |
確定世界 |
素世界 |
局在世界 |
|
状態粒子 |
確定状態粒子 |
素状態粒子 |
局在状態粒子 |
|
世界粒子 |
確定世界粒子 |
素世界粒子 |
局在世界粒子 |
|
経路 |
確定経路 |
素経路 |
局在経路 |
|
事象 |
確定事象 |
素事象 |
局在事象 |
|
歴史 |
確定歴史 |
素歴史 |
局在歴史 |
12 謝辞
本論文を作成するにあたり、貴重な助言を頂いた、TYさんとNSさんに心より感謝いたします。