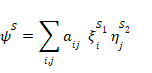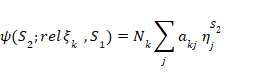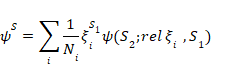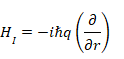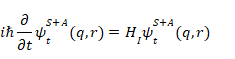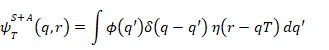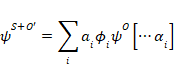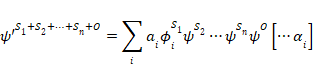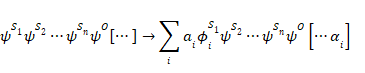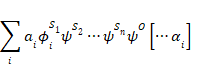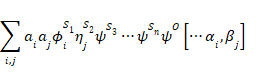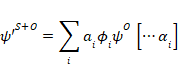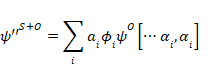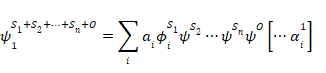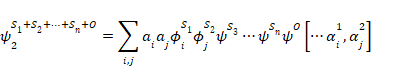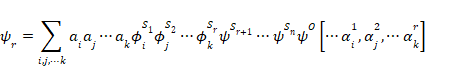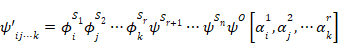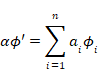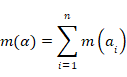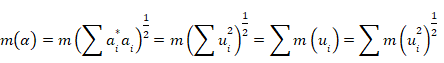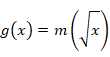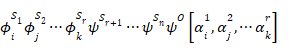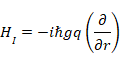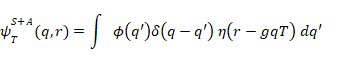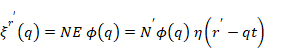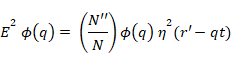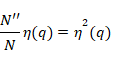エヴェレットの多世界解釈の論文

2019/11/24

[リスト]

公開日 2019/2/11

K. Sugiyama

多世界解釈の元になったエヴェレットの論文は翻訳されていないため、読んだことがない方も多いと思います。そこで彼の論文を翻訳し公開することにしました。本論文は多世界解釈の基本事項を理解するうえで役立つものと考えます。

元の論文の4章と5章の内容は、節に分離されていませんが、理解のしやすさを考慮し節で分離しました。以下、分離した各節について簡単に解説します。

4.1 相対状態の定式化

相対状態とは、観測者と観測対象の複合系において、観測者からみた波動関数を複合系から切り取ったものです。次の図のように系S₁のk番目の固有状態から見た、系S₂の固有状態の番号jについての波動関数が相対状態となります。

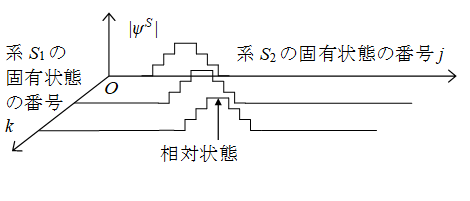
多粒子波動関数

図1: 相対状態

4.2 フォン・ノイマンの測定過程

フォン・ノイマンの測定過程とは、測定対象物の位置によって、測定器の針が移動する過程のことです。次の図のように最初、測定器の針の位置rの波動関数はゼロ付近に集中していますが、測定によりqの値に依存して広がります。

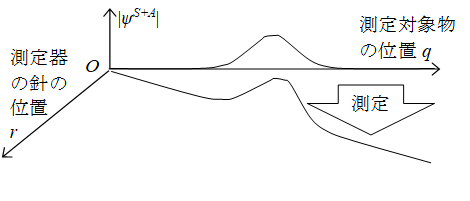
多粒子波動関数

図2: フォン・ノイマンの測定過程

5.1 観測者の記憶系列

観測者の記憶系列とは、一連の観測結果が記録された記憶装置のことです。この記憶装置は波動関数のように重ね合わせられるため、量子コンピュータの量子ビット列を思い浮かべるのがよいと考えます。次の図のように、量子ビットをn個並べ、測定するたびにその結果を量子ビットに記録します。その結果、観測者の記憶系列は波動関数となります。

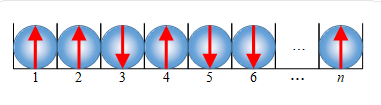
多粒子波動関数

図3: 観測者の記憶系列

5.2 観測者の分岐

記憶系列の異なる観測者は、異なる経験をしてきました。それは観測者が分岐したことを意味します。分岐した観測者は各世界に同時に存在することとなります。

5.3 測度の導入

エヴェレットは、1957年に発表されたグリーソンの定理と同様の方法で測度を導入しました。この測度を一意に定義するには、基底を一意に選択する方法が必要です。しかし、スピンなどでは適当な方法のないことが、1990年のエイドリアン・ケントの論文で批判されました。(多世界解釈の基底問題)

5.4 測度と確率の対応関係

記憶系列の測度というものを考えた場合、測定回数を増やすと、ある特定のケースを除き、ほとんどのケースで測度がゼロとなります。残ったある特定のケースでは、分布がボルンの規則と一致するという論法をエヴェレットは採用しました。確かにこの論法は正しいですが、測度の物理的意味が明確でありません。実際、1990年のエイドリアン・ケントの論文ではこの点を批判しました。(多世界解釈の確率問題)

5.5 観測結果の相関

EPRのパラドックスを提示し、観測者の記憶系列がそれと矛盾しないことを論証しています。

本記事は、次のサイトで公開されているエヴェレットの論文を元に翻訳しました。

Relative State Formulation of Quantum Mechanics - Semantic Scholar

2019.2.11 K. Sugiyama

量子力学の「相対状態」定式化 [1] [2]

1957/7/1

ヒュー・エヴェレット3世 [3]

(K. Sugiyama訳)

1 はじめに... 4

2 量子力学の従来の「外部観測」定式化の適用範囲... 5

3 孤立系の内部にある量子力学... 6

4 相対状態の概念... 7

4.1 相対状態の定式化... 7

4.2 フォン・ノイマンの測定過程... 9

1 はじめに

一般相対論を量子化するために、時空の基本構造自体を量子化しようとすると、量子力学の現在の定式化と解釈の意味について深刻な疑問が生じる。この論文は量子力学の基礎を明確にしようとするものである。本論文は一般相対論への応用に適しているとされる形式での量子論の再定式化を提案する。

その目的は従来の量子論の定式化を否定あるいは反証することではない。なぜなら、従来の量子論は圧倒的に多様な問題で有用であること実証してきたからだ。むしろ、その目的は、従来の解釈を導出できるような完全で一般的な新しい定式化を提供することである。

したがって、この新しい定式化と古い定式化の関係は、理論に対するメタ理論の関係にあたる。つまり新しい定式化とは、古い理論の特徴と一貫性および適用範囲を調査し、明確化できる基礎となる理論である。

新しい理論は、従来の理論からの根本的な逸脱に基づくものではない。古い理論における観測を扱う特別な仮説（訳者注：ボルンの規則のこと）は、新しい理論では省略される。それによって、変更された理論は新しい特徴を獲得する。その新しい理論が分析され、その理論でその理論自身を分析することによって、理論の量と経験的な世界の特性との間のあらゆる識別が可能になる。そのような識別がなされることで、その役割と論理的位置づけを明確化する方法により、新しい理論で省略されていた「従来の理論における観測を扱う仮説」が導かれることとなる。

我々は、従来の定式化と修正を求める動機を簡単に説明することから始めることとする。

2 量子力学の従来の「外部観測」定式化の適用範囲

我々は量子力学の従来の「外部観測」形式を本質的に次のように考えている[4]。

物理系はヒルベルト空間の要素であり、外部の観測者により系で行われる様々な観測結果の確率を計算するための情報を与える状態関数ψによって完全に記述される。状態関数を変更する方法として、根本的に異なるふたつの方法がある。

過程1：固有状態 ₁, ₂,…を有する状態ψの量を観測することでもたらされる不連続な変化。状態ψは確率 |(ψ, _j)|² で状態 _j に変化する。

過程2：波動方程式 ∂ψ / ∂t = Aψ に従う孤立系の、連続的かつ決定論的な状態変化。ここで、Aは線形演算子である。

この定式化は豊富な結果を記述しており、これまでにそれと矛盾する実験的証拠は知られていない。

しかしながら、考えられるすべての状況がこの数学的定式化の枠組みに適合するわけではない。例えば、観測者あるいは測定装置と、対象系からなる独立した系を考えてみよう。系全体の状態の時間的変化は、過程2で説明できるだろうか。もしできるのであれば、過程1のような不連続な確率的過程は起こり得ないと思われる。もしできないのであれば、観測者を含む系は、我々が他のすべての物理系で認めている量子力学的記述に支配されていないことを認めざるをえない。この問題は心理学の領域にあると除外することは決してできない。量子力学における「観測者」の議論の多くは、光電池、写真乾板、および機構的なふるまいについて議論の余地のない類似の装置に関係している。より一般的な意味での観測者を機構的なレベルで分析したくない場合は、次の方法でこの種の問題を限定できる。

近似測定のみが行われる場合、つまり装置や観測者と対象系の間の相互作用が弱く限られている場合、従来の過程1および過程2のどのような混合物を適用すべきだろうか。近似測定の場合、適切な理論は次の(1), (2)を指定する必要がある。

(1) 装置の特定の読み取り値に対応する対象系の新しい状態

(2) この読み取り値が発生する確率

フォン・ノイマンは射影演算子の方法で近似測定のある特別なクラスを取り扱う方法を示した[5]。しかし、射影演算子の方法によるすべての近似測定値の一般的な扱いは不可能であることを示すことができる。(4章参照)

量子力学の従来の定式化を時空の構造にどのように適用するのだろうか。この問題は、閉じた宇宙の場合、特に深刻となる。閉じた宇宙を観測するために系の外側に立つ場所はない[6]。ある状態から別の状態への遷移を生成するための外側は存在しない。エネルギーの適切な状態というおなじみの概念でさえ、まったく適用できない。エネルギー保存則の導出では、系と相互作用の全部分を含む十分な大きなの表面にわたる積分で全エネルギーを定義する[7]。しかし閉じた空間では、より大きな体積を表面が含むようになるにつれて、最終的にエネルギーは消え去ってしまう。つまり、閉じた空間の全エネルギーを定義する試みは、「ゼロはゼロに等しい」という空虚な声明におちいることとなる。

閉じた宇宙、近似測定、そして観測者を含む系の量子的な記述はどのように行われるのだろうか。これら3つの質問には共通のひとつの特徴がある。それらはすべて、孤立した系の内部にある量子力学について質問しているということだ。

従来の方法で定式化された量子力学を、外部観測の対象とならない系に適用できないことは明らかだ。なぜなら、その定式化の全体的な解釈体系は、外部観測の概念に基づいているからだ。観測のさまざまな結果の可能性は、もっぱら過程1によって規定されている。定式化のその部分がなければ、従来の機構に物理的な解釈を与えることはできない。しかし、過程1は、外部からの観測を受けない系にとっては問題外である[8]。

3 孤立系の内部にある量子力学

この論文は完全な理論として純粋な波動力学(過程2のみ)を採用することを提案する。本論文は、あらゆる場所で常に線形の波動方程式に従う波動関数が、孤立した物理系のための完全な数学モデルを例外なく提供できると仮定する。本論文はさらに、外部からの観測を受けるすべての系は、より大きな孤立系の一部とみなせると仮定する。

波動関数は、先験的な解釈を必要とせず、基本的な物理的実体とみなされる。解釈は、理論の論理構造の分析後にのみ現れる。ここでも、いつものように理論自体がその解釈のための枠組みを決定する[9]。

どのような解釈においても、理論の数学的モデルを経験と一致させる必要がある。この目的のため、理論自体の中で物理系として扱える観測者のための抽象モデルを定式化し、他の部分系と相互作用する観測者を含む孤立系を検討し、周囲の部分系との相互作用の結果として観測者に生じる変化を推測し、経験を語る身近な言語の変化を解釈する必要がある。

第4章では、構成要素としての部分系の状態という観点から複合系の状態の表現を詳細に調べる。数学は、次の意味で状態の相対性という概念を認識させるように導く。すなわち、構成要素としての部分系は、複合系の残りの部分と無関係な状態に、つまり単一の明確に定義された状態にあるとは言えない。任意に選択された、部分系の状態は、複合系の残りの部分の相対状態と一意に対応する。通常、この相対状態は最初の部分系の状態の選択に依存して異なる。したがって、ひとつの部分系の状態は独立した存在ではなく、残りの部分系の状態によってのみ固定される。言い換えれば、部分系が占める状態は独立しているのではなく、相関している。系間のこのような相関関係は、系が相互作用するたびに発生する。現在の定式化において、すべての測定と観測の過程は単純に、関係する物理系間の相互作用、すなわち強い相関を生み出す相互作用とみなされるべきである。フォン・ノイマンによる簡単な測定モデルは、この観点から分析されている。

第5章では、観測問題をより抽象的に扱う。その結果が最大の一般性を持ち、これらの原理が成り立つあらゆる形態の量子論に適用するため、重ね合わせの原理と、複合系状態が部分系状態から形成されるという一般規則のみを採用する。対象系の状態と関連付けられる観測者の状態が推論される。観測者(磁気テープ記憶装置、計測装置など)の経験は、過程1に基づく量子力学の従来の「外部観測者」による定式化の予測と完全に一致していることがわかる。

第6章では、量子力学の「相対状態」の定式化について要約する。

4 相対状態の概念

4.1 相対状態の定式化

我々は今、複合系の波動力学の定式化の一連の結果を詳細に調べる。複合系Sが、関連するヒルベルト空間H₁およびH₂を有するふたつの部分系S₁およびS₂から構成される場合、複合系の通常の定式化にしたがって、Sに対するヒルベルト空間はH₁およびH₂のテンソル積 ( H = H₁⊗H₂ と記述される) であるとみなされる。これは、集合 {ξ_i^S¹} と {η_j^S²} がそれぞれS₁とS₂の完全な正規直交状態の集合である場合、Sの一般的な状態は重ね合わせとして記述できるという結論を表している。

(1)

式(1)より、Sは明確な状態 ψ^Sにあるが、部分系S₁とS₂は、互いに独立した明確な状態にない。(ただし、a_ij のうちのひとつを除くすべてがゼロであるような特別な場合を除く)

しかし、ある部分系で選択する任意の状態に対し、もう一方の部分系の相対状態を一意に割り当てることが可能である。たとえば複合系Sが式(1)で与えられる状態 ψ^S にあるときに、部分系 S₁ の状態として ξ_k を選択する場合、対応するS₂の相対状態 ψ(S₂;rel ξ_k ,S₁) は次のように表現できる。

(2)

ここで、N_k は規格化定数である。ξ_k に対する相対状態は、ξ_k の直交補空間の基底 {ξ_i} (i≠k) の選択とは無関係であるため、ξ_k だけによって一意に決定される。したがって、 S₁ の任意の状態に対する S₂ の相対状態をみつけるためには、S₁ の基底の一要素である所望の状態を含むような、 S₁ と S₂ の基底の任意の対を使用して上記の手順を実行する。S₂ の状態に対して S₁ の状態を見つけるには、手順の中で S₁ と S₂ を入れ替える。

系S₁の状態が、 ^S1 の状態であることが測定の結果からわかっているとき、従来の「外部観測」定式化では、系S₁の状態 ^S1 に対するS₂の相対状態 ψ(S₂;rel ,S₁) は、S₂のすべての測定結果に対する条件付き確率分布を与える。つまり、^S1は観測された固有値に対応するS₁における測定の固有関数である。

S₁の任意の基底 {ξ_i} に対し、Sの状態をS₁の基底 {ξ _i} から構成した状態とS₂の相対状態の対の単一の重ね合わせとして表すことが常に可能である。したがって、式(2)から式(1)は次の形式で記述できる。

(3)

これはよく使われる重要な表現である。

要約すると、一般に複合系のひとつの部分系に対する単一の状態のようなものは存在しない。部分系は、系の他の部分の状態から独立している状態を持たないため、部分系の状態は一般に互いに相関している。ひとつの部分系の状態を任意に選択し、残りの部分の相対状態を導くことができる。したがって、我々は状態の根本的な相対性に直面しており、それは複合系の数学形式によって暗示されている。部分系の絶対状態を尋ねることに意味はない。部分系の残りの部分の与えられた状態に関連した状態だけを質問できる。

4.2 フォン・ノイマンの測定過程

この時点で、フォン・ノイマンによる簡単な例を考えよう。これは測定過程のモデルとして機能する。この例の議論は「観測」の分析のための基礎を準備する。単一の座標 q （粒子の位置など）、および単一の座標 r (たとえば計測器の針の位置など)の装置から構成される系から始める。それらは初期状態では独立していると仮定する。

そのため、その合成波動関数は ψ₀^S+A (q, r)= (q) η(r) と表現できる。ここで、(q) は初期状態の波動関数であり、η(r) は初期状態の装置の関数である。ハミルトニアンは、ふたつの系が t = 0 から t = T までの区間を除いて相互作用しないようになっている。この間、ハミルトニアンは次の式(4)のような単純な相互作用のみで構成される[10]。

(4)

このとき、次の状態[11]

(5)

は、時刻t = 0に指定された初期状態にあったという条件で、次のシュレーディンガー方程式の解となっている。

(6)

時刻 t ＝ T (相互作用が停止する時点) の式(5)から、明確に独立した装置の状態、すなわち独立した系の状態は存在しないことがわかる。したがって、この装置は明確な対象系の値を示すことは決してなく、過程1のようなことも起こらない。

それにもかかわらず、我々は合成波動関数(5)を対の部分系の状態の重ね合わせとして見ることが可能であり、その各要素は明確なqの値と、それに対応して変位した装置状態を有する。したがって、相互作用の後、状態(5)は次の形式になる[12]。

(7)

これは状態 ψ_q' (q, r) = δ(q−q') η(r −qT)の重ね合わせである。

重ね合わせの各要素 ψ_q' (q, r) は、系が明確な値 q = q' を有し、装置が元の状態から量 q'T だけ変位した状態を有する状態を表す。次に、これらの要素 ψ_q' (q, r) は全体の状態(7)を形成するために係数 (q') とともに重ね合わされる。

逆に、装置の座標 r = r' が明確な表現に変換すると、式(5)は次のように記述できる。

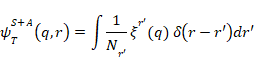
ここで、関数ξ ^r'(q)は定値 r = r' の装置状態 δ(r − r') に対する相対系の状態の関数である[13]。

(8)

また、規格化定数 N_r' は次の通り。

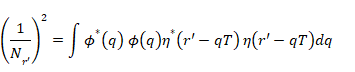
Tが十分に大きい、または η(r) が十分に鋭い (δ(r) に近い) 場合、ξ ^r'(q) はほとんど δ(q−r' / T) となり、相対系状態 ξ ^r'(q)は、ほとんど値 q = r'/ T の固有状態となる。

我々は、式(8)が状態 ψ_r' の重ね合わせ状態にあり、その各々に対して装置が明確な値 r' を記録し、系が q ＝ r' / T に対応する測定値のほぼ固有状態のままであることを見てきた。したがって、固有状態への不連続な「跳躍」は、全体の波動関数の重ね合わせへの分解方法に依存し、特に選択された装置の座標値に対する相対的な命題にすぎない。その完全な理論が関係している限り、重ね合わせのすべての要素が同時に存在し、過程全体は非常に連続的である。

フォン・ノイマンの例は、より一般的な状況の特別な一例にすぎない。任意の対象系と相互作用する任意の測定装置を考えよう。相互作用の結果として、測定装置の状態はもはや独立して定義できない。対象系の状態に関連してのみ定義できる。言い換えれば、ふたつの系の状態間には相関関係しかない。そのような測定では、何も決めることができないように感じられる。

物理対象は常に明確な位置を持っているように見えるので、この不確定な振る舞いは我々の観測とは、かけ離れているように感じられる。純粋に過程2に基づいて構築されたこの特徴的な波動力学理論を経験と調和させることができるだろうか。それともこの理論は許容できないものとして放棄するしかないのだろうか。この質問に答えるため、我々は理論の枠組みの中で観測それ自体の問題を検討することとする。

5 観測

5.1 観測者の記憶系列

純粋に物理的な系と見なされ、かつその理論の枠内で扱われる観測者に対して起こる現象を、我々は推論する必要がある。これを達成するためには、観測者の過去の経験の特徴を用いてそのような観測者の現在の特性のいくつかを識別する必要がある。

したがって、観測者Oが事象αを観測したと言うためには、Oの状態がその前の状態からαに依存する新しい状態に変化したことが必要となる。

そのためには、観測者が記憶 (すなわち、観測者の過去の経験と一致する状態を有する比較的恒久的な性質の一部) を有することを観測者が考慮することで十分であろう。観測者の過去の経験について推論するためには、それが数学的モデル内に現れるように現在の記憶の内容を推論することで十分である。

観測者のモデルとして、もし望むならば、自動的に行動する機械、感覚装置を有し、過去の感覚データおよび機械構成を登録できる記録装置に結合することを検討できる。我々はさらに、その機械の現在の行動が、その機械の現在の感覚データだけではなく、その記憶の内容によっても決定されるように構成される場合を検討できる。そのような機械は、一連の観測 (測定) を実行でき、さらに過去の結果に基づいて将来の実験を決定できる。現在の感覚データと機械構成がすぐに記憶装置へ記録されるとすれば、ある瞬間における機械の動作は、その記憶内容のみの関数とみなすことができる。そして機械のすべての関連した経験は記憶に含まれる。このような機械では、Aの出現が記憶に表示されている場合、「機械はAを認識した」または「機械はAを認識している」などの言い回しを使用する。実際、主観的な経験を表現する日常的な言葉はすべて、そのような機械によく当てはまる。そして、そのような言葉は、複雑な自動装置を扱う個人にはよく知られていることだが、機械の動作を扱うための最も自然で有用な表現様式を形成する。

量子力学的に観測者を表す系を扱うとき、我々はそれを状態関数ψ^Oに帰属させる。状態ψ^Oが、事象A, B, …, C の表現を記憶に含む観測者を記述している場合、記憶系列をかっこ内に下付き文字として追加することで、この事実を表現する[14]。

(9)

我々が時間的に順序付けされていると仮定する記号 A, B, …,C は、それ故、観測者の過去の経験と一致する記憶構成を表す。これらの構成は、紙テープの打ち抜き、磁気リールへの圧痕（あっこん）、リレースイッチ回路の構成、あるいは脳細胞の構成とさえ見なすことができる。我々は、それらの記憶構成によって「観測者は一連の事象 A, B, …,C を経験した」と解釈可能であることを要求する。(我々は時々、検討しているケースとは無関係な過去の記憶の存在の可能性を示すため、記憶系列 …A, B, …,Cのように三点リーダーを記述することがある)

数学的モデルは、そのような観測者の系と他の物理系との相互作用(観測)を、過程2の波動力学の枠内で扱うことを目指す。その結果として生じる記憶構成を推測することは、観測者の過去の経験の記録として解釈されるべきである。

我々は「良好な」観測を構成するものを定義することから始める。初期状態がψ^Oである観測者による、系Sの固有関数 _i を持つ量Aの良好な観測は、指定された期間内に各(合計)状態

(10)

を新しい状態

(11)

に変換する相互作用から構成される。ここでα_iは状態 _i を特徴づける記号である[15]。(例えば、記号α_iは固有値の記録を表すかもしれない)

つまり、次の(1), (2) を要求する。

(1) 対象系の状態は、もしそれが固有状態であれば、変化しないこと

(2) 観測者の状態は、系の状態がどの固有関数であるかを「知っている」ような状態に変化すること

固有値など _iを特徴付けるいくつかの特性が観測者の記憶装置に記録される。このときに、系の固有状態が変化しないという要件は、観測値が有意（再現可能）であるために必要である。また、相互作用を観測と呼ぶことができるのであれば、観測者の状態が固有関数ごとに異なる方法で変化するという要件を必要とする。

一般的な相互作用がどの程度良好な観測の定義を満たすかは、次の(1),(2)に依存する。

(1) 相互作用が観測者系の動的変数(記憶変数を含む)と対象系の動的変数に依存する方法

(2) 観測者系の初期状態

上記の(1)と(2)が与えられると、再現性の仮定によって要求されるように、例えば波動方程式を解き、相互作用の終了後の複合系の状態を推定し、元々固有状態にあった対象系が固有状態のままか検証できる。この仮説は例えば、すでに議論されたフォン・ノイマンのモデルによって満たされている。

良好な観測の定義から、観測の固有状態にない系での観測の結果を最初に推論する。我々の定義から、相互作用は状態 _iψ^O[…] を_iψ^O[…α_i] に変換する。結果として、波動方程式のこれらの解は、任意の初期系状態について最終状態を与えるために重ね合わせることができる。したがって、初期系状態が固有状態ではなく一般の状態 Σ_i a_i_i である場合、最終的な全体の状態は次の形式になる。

(12)

この重ね合わせの原理は、測定中に相互作用しない系の存在下でも適用され続ける。したがって、系S₁, S_2,…, S_n はOと同様に存在し、元の状態ψ^S¹, ψ^S²_,…, ψ^Snであり、測定時間中の唯一の相互作用がS₁とOとの間で起こると、測定は初期の全体の状態

(13)

を最終的な次の状態へ変換する。

(14)

ここで、a_i = (_i^S¹, ψ^S¹)であり、_i^S¹は観測対象の固有関数である。

こうして、観測過程が発生する系を記述する全体的な状態関数の変換に関する一般規則にたどり着く。

規則1：観測者Oによる系S₁内の固有関数 _i^S¹を有する量Aの観測は、全体の状態を次のように変換する。

(15)

ここで、a_iは下記である。

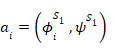
次に、全体状態が重ね合わせになっている2番目の観測を検討する場合、各要素は別々に波動方程式に従い、残りの要素とは無関係に動作するため、重ね合わせの各要素に個別に規則1を適用できる。次に結果を重ね合わせて最終的な解を求める。これを次のように定式化する。

規則2：規則1は、系全体の状態の重ね合わせの各要素に別々に適用でき、その結果は最終的な全体の状態を得るために重ね合わされる。したがって、観測者OによるS₂上の固有関数 η_j^S² を用いたBの決定は、全体の状態

(16)

を次の状態に変換する。

(17)

ここで、b_j = (η_j^S2, ψ^S²) であり、これは各要素 _i^S¹ ψ^S2…ψ^Snψ^O[…α_i] への規則1の適用により生じ、その結果は係数a_iで重ね合わせられる。

重ね合わせの原理から直接導かれるこれらふたつの規則は、あらゆる組み合わせにおけるあらゆる数の観測過程について最終的な総状態を決定するための便利な方法を与える。我々は今、そのような最終的な全体状態の解釈を要求している。

初期状態がψ^O[…] である観測者Oが、初期状態ψ^Sの系Sにおける固有関数 _i を持つ量Aの単純な観測の場合を考えてみよう。最終的な結果は、これまで見てきたように、次のような重ね合わせとなる。

(18)

対象系と観測者系は1対1の対応で相関しており、もはや独立した系状態または観測者状態はない。しかしながら、重ね合わせの各要素 _iψ^O[…α_i] において、対象系の状態は観測の特定の固有状態となっており、さらに観測者系の状態は、観測者がその特定の対象系の状態を確実に認識しているものとして記述する。この相関関係は、測定が行われたという解釈を維持することを可能にするものである。

ここで、観測者系がもう一度対象系と相互作用する状況を考える。規則2によると、2回目の観測の後、我々は次のような全体の状態に到達する。

(19)

また、各要素 _iψ^O[…α_i, α_i] は系固有状態を表すが、今回はふたつの観測値のそれぞれについて同じ結果が得られた観測者も表す。したがって、最終的な重ね合わせにおける観測者のあらゆる別々の状態に対して、観測の結果は、異なる状態に対しては異なっていても再現可能であった。この再現性は、観測後に特定の観測者状態に対する相対的系状態が対応する固有状態であるという事実の結果である。

5.2 観測者の分岐

今度は、別の状況を考えてみよう。初期状態が ψ^O[…] である観測者Oは、最初は同じ状態にある別々の

同一系 ψ^S¹ = ψ^S² = … = ψ^Sn = Σ_i a_i_i において、同じ量Aを測定する初期の全体の状態関数は、次のようになる。

(20)

(ここで_i は通常通りAの固有関数である)

系の測定はS₁, S₂, …, S_nの順序で実行されると仮定する。最初の測定の後の全体の状態は規則1によって次のようになる。

(21)

(ここで、α_i¹は第1の系S₁を指す)

2回目の測定の後の全体の状態は規則2によって、次のようになる。

(22)

そして一般に、r回の測定が行われた (r ≤ n) 後、規則2は次のような結果を与える。

(23)

この状態ψ_rは次のように解釈できる。つまり、その状態は次の状態の重ね合わせで構成される。

(24)

各観測者は、明確な記憶系列 [α_i¹, α_j²,…α_k^r ] を保持している。

観測者に関連する(観測された)系の状態は対応する固有関数 _i^S¹ _j^S² _k^Sr であり、残りの系 S₁, S₂, …S_nは変更されない。

最終的な重ね合わせの典型的な要素 ψ'_{ij... k} は、観測者が観測について明らかに乱数的な一連の明確な結果を知覚した状況を記述している。さらに、対象系は観測の対応する固有状態に残されている。この段階で、以前の系 (S_ℓ) の観測値の再決定が行われると仮定する。その結果、最終的な重ね合わせのすべての要素は、観測者を [α_i¹,… α_j^ℓ,…α_k^r ,α_j^ℓ] という形式の記憶構成で記述する。このように前の記憶と後の記憶が一致する、すなわち記憶状態が相関している。したがって、重ね合わせの典型的な要素によって説明されるように、観測者には、系上の各初期観測は系を乱数的に固有状態へ「跳躍」させ、その後同じ系での後続の測定のためにそこに留まるように見える。したがって、相対頻度の定量性に関する質問を今のところ無視して、過程1の確率論的主張は、最終的な重ね合わせの典型的な要素によって説明される観測者にとって有効であるように見える。

一連の観測過程を通して、観測者を表す物理系はひとつだけであるが、(相互作用系の表現から生じる) 観測者は一意な状態にない。それにもかかわらず、重ね合わせの表現が存在し、その各要素は明確な観測者状態と、対応する系の状態を含む。したがって、後続の観測(または相互作用)のたびに、観測者の状態は多数の異なる状態に「分岐」する。各分岐は、測定の異なる結果と、対象系の状態に対応する固有状態を表す。すべての分岐は、与えられた一連の観測の後の重ね合わせに同時に存在する[16]。

一連の測定を実行する観測者の記憶構成の「軌跡」は、線形構成の記憶構成ではなく分岐木であり、そのすべての結果が得られる。各分岐は数学モデルに依存する係数による最終的な重ね合わせとして同時に存在する。もし身近な記憶装置だったら、分岐は無期限には継続せず、記憶容量により制限されるため停止する必要があるだろう。

5.3 測度の導入

定量的な結果を確立するため、最終的な重ね合わせの要素にある種の測度(重み付け)をかける必要がある。これは、重ね合わせの要素によって記述されるほとんどすべての観測者状態を保持する主張を生成可能とするために必要である。我々は典型的な観測者状態について、観測の異なる可能性のある結果( 記憶装置に記録されている)の相対頻度について定量的な説明をしたい。しかしこれを達成するには、直交状態の重ね合わせから典型的な要素を選択するための手法が必要である。

したがって、我々は直交状態 Σ_i a_i_i の重ね合わせの要素に測度を割り当てるための一般的な手法を求める。重ね合わせの要素の複素係数を引数とする正の関数 m が必要である。そのため、 m(a_i) は要素 _i に割り当てられた測度になる。この一般的な手法を明確にするには、まず状態自体が規格化されていることを最初に要求する必要がある。そうすれば係数と状態を区別できる。ただし状態を区別したとしても、任意の位相を持つ係数までしか係数を決定できない。したがって、位相のあいまいさを避けるため関数mは振幅の複素係数の絶対値だけの関数、すなわち m(a_i) = m(|a_i|) でなければならない。

我々は測度に対しさらに加法性の要件を課す。また、我々は重ね合わせ Σⁿ_i₌₁a_i _iの部分集合を次のように単一の要素α'とみなす。

(25)

次に、 ' に割り当てられた測度が _i に割り当てられた測度の合計であることを要求する。(iは1からnまでとする)

(26)

このときすでに、mの選択は振幅の絶対値の二乗だけに制限されている。言い換えれば、かけられる係数は別として、 m(a_i) = a_i^* a_i が成り立つ。

これを見るため、 ' の規格化が次の式を要求することに注意しよう。

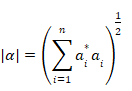
mが振幅に依存するという我々の所見から、我々はa_iをそれらの振幅u_i = |a_i| に置き換える。式(26)は次の要件を課す。

(27)

ここで、新しい関数 (x) を定義する。

(28)

式(27)は次の式を要求している。

(29)

したがって、 (x) は線形に制限され、必然的に次の形式を取る。

(30)

ここで、cは定数である。したがって、

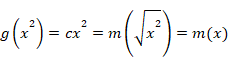
となり、mは次の形式に制限されると推定される。

(31)

このようにして、加法性の要件と一致する唯一の測度の選択は、必要に応じ規格化要件により固定される定数である係数cは別として、振幅の絶対値の二乗であることを示した。(測度の合計が1になるという要件は、この定数が1であることを意味する)

ここでの状況は、古典的な統計力学とよく似ている。そこでは位相空間自体に測度を置き、それからいくつかの主張(エルゴード性、準エルゴード性など)を行うことによって位相空間内の系の軌跡に測度を置いた。これは「ほとんどすべて」の軌跡に当てはまる。この「ほとんどすべて」の概念は測度の選択にも依存する。この場合、位相空間上のルベーグ測度であると見なされる。それにもかかわらず、位相空間上のルベーグ測度の選択は、「確率の保存」が成り立つ唯一の選択であり（リウヴィルの定理）、したがって合理的な統計的推論を可能にする唯一の選択であるという事実によって正当化できる。

我々のケースでは、観測者の「軌跡」について述べたいと思う。しかし我々にとって軌跡は、連続する測定ごとに常に分岐している(状態から重ね合わせへの変換)。古典的な場合における「確率の保存」に類似した要件を有するため、ある時点で軌跡に割り当てられた測度が、後でその別々の分岐の測度の和に等しくなることを要求する。これはまさに我々が課した加法性要件であり、これは独自に振幅の絶対値の二乗の測定を選択することにつながる。したがって、我々の手続きは古典的な統計力学の手続きとまったく同じように正当化される。

5.4 測度と確率の対応関係

我々の要求を満たすであろう独特の測度、振幅の絶対値の二乗の測度があると推論したので、我々は推論を続ける。次に我々は重ね合わせである式(24)のi, j, … k th の要素

(32)

に次の測度(重み)を割り当てる。

(33)

記憶構成 [α_i¹, α_j²,…α_k^r] を持つ観測者の状態には、測度 a_i^*a_i a_j^*a_j…a_k^*a_k = M_ij_…k が割り当てられる。我々はすぐにこれが測度の積であることを見る。

(34)

ここで M_ℓ は以下の通り。

その測定値が特定の記憶系列 [α_i¹, α_j²,…α_k^r ] は、単に記憶系列の個々の構成要素に対する測度の積である。

我々の測度構造は乱数系列の確率論と直接の対応関係がある。もし我々がM_ij_…kを系列に対する確率とみなすならば、系列は各項に独立した確率 M_ℓ = a_ℓ^*a_ℓ を割り当てることによって生成される乱数系列と等価となる。確率論は測度論と数学的に等価であるため、確率論のすべての結果は測度論の言葉に翻訳されるべきことを念頭に置いたうえで、確率論を利用できる。

したがって、特に、系列がますます長くなる(より多くの観測が行われる)ならば、観測回数が無限に増えるにしたがい合計の測度がゼロに向かう傾向がある集合を除き、最終的な重ね合わせの記憶系列は、独立した確率 a_ℓ^*a_ℓ によって乱数的に生成された系列に対する基準を満たす。

したがって、頻度の特別な場合を含む、あらゆる記憶系列にわたる関数のすべての平均は、測度がゼロの記憶系列の集合を除いて、確率a_i^*a_iから計算できる。したがって、観測回数が無限大になるにつれて、過程1の統計的主張は、重ね合わせのほとんどすべての要素(24)において、観測者に有効であるように見えることを示した。

これまで同一の系で同一の量の一連の観測値のみを検討してきたが、より一般的な一連の測定値を記述し、ここで提示してきた方法と同じ方法で規則1と2を適用することにより、その結果を検証できる。

したがって、観測の順序が任意である場合、これらの観測が同じまたは異なる系で任意の順序で行われる場合、および各系の各数量の観測回数が非常に多い場合の状況をまとめることができる。

ほぼゼロの記憶系列の集合を除き、ある系の各初期観測に対して過程1で与えられた独立した確率と、一連の観測を実行するための通常の遷移確率を使用して、記憶系列全体の関数の平均を計算できる。観測回数が有限回の間は、すべての種類の観測値の回数が無限大になるにつれて、計算は正確になり、例外的な集合の測度はゼロになる。

5.5 観測結果の相関

個々の要素に割り当てられた確率によって記憶系列にわたる平均を計算するためのこの規定は、まさに従来の「外部観測」理論(過程1)のそれである。さらに、これらの予測は、ほとんどすべての記憶系列に当てはまる。したがって、通常の理論のすべての予測は、ほぼすべての観測者状態において、観測者に有効であるように見える。

特に、不確定性原理には、系上の最新の測定値が相対的な系状態に関するすべての可能な情報を提供することから、系の初期の観測結果と一連の観測値との間に直接の相関がないことから、違反しない。

量Aの2つの連続した観測の間（すべて同じ系での観測）の量Bの観測は、Aの結果に対する前の記憶状態と後の記憶状態の間の1対1の対応関係を破壊する。

したがって、異なる量の交互観測では、同じ観測量に対する記憶状態間の相関には基本的な制限があり、これらの制限は不確定性原理の内容を表している。

最後の段階として、複数の観測者系が同じ対象系と相互作用する(観測する)こと、および互いに相互作用する(通信する)のを許可することの結果を調査できる。後者の相互作用は、ある観測者の記憶構成の一部を別の観測者と相関させる単なる相互作用として扱うことができる。これらの観測者系を調べたとき、規則1と2を使ってこの章で示したのと同じ方法で、最終的な重ね合わせのすべての要素で次の(1),(2),(3)がわかる。

(1) 何人かの観測者が対象系内で同じ量を別々に観測し、次に結果を互いに伝達し合うと、彼らは一致していることを発見する。観測を行った別の観測者によって結果が彼に伝達された後に観測者が観測を行ったときでさえも、この合意は持続する。

(2) ひとりの観測者に対象系で量Aの観測を実行させ、次にこの対象系でAと交換しない量Bの観測を実行させ、最後に最初の観測者にAの観測を繰り返させる。その場合、最初の観測者の記憶系は、一般に、両方の観測に対して同じ結果を示すことはない。他の観測者による交換しない量Ｂの介在的な観測は、Aのふたつの観測間の一対一の相関の可能性を防止する。

(3) ふたつの対象系の状態が相関しているが、ふたつの系が相互作用していない場合を考える。ある観測者に最初の系で指定された観測を実行させ、次に別の観測者に2番目の系で観測を実行させ、最後に最初の観測者に彼の観測を繰り返させる。そして、最初の観測者は常に同じ結果を得て、2番目の観測者による観測は最初の観測の結果にはまったく影響を及ぼさないことがわかる。このような相関する非相互作用系に関係するアインシュタイン、ポドルスキー、ローゼンの架空のパラドックス[17]は、容易に調査され、本手法で明確にされている。

現在の枠組みの中で、いくつかの観測者と系のさらに多くの組み合わせを研究できる。現在の「相対状態」形式の結果は、その身近な機構が適用可能なすべての場合において、従来の「外部観測」形式の結果と一致する。

結論として、複合系の状態関数が継続的に時間発展することで、理想化された観測者を含む過程の完全な数学モデルが得られる。相互作用が起こると、時間的進化の結果は状態の重ね合わせになり、その各要素は観測者の記憶に異なる状態を割り当てる。ほとんどすべての観測者状態における記憶の状態から判断して、量子論の通常の「外部観測」定式化の確率論的結論は妥当である。言い換えれば、最初の確率に関する主張がない純粋な過程2の波動力学は、おなじみの形式主義のすべての確率概念につながる。

6 考察

純粋な波動力学に基づく理論は概念的に単純な因果理論であり、それは経験と一致する予測を与える。それは、測定過程それ自体と数人の観測者の相互関係のような、時には不可解な多くの主題を詳細に、数学的にそして論理的に一貫した方法で調査できる枠組みを構成する。その確率論的特徴は、理論自体から導き出されるのではなく事前に仮定されるという理由により、従来の量子論の「外部観測」定式化に対する反論がこれまで提起されてきた。現在の「相対状態」の定式化は、標準的な定式化のすべての内容を保持しながら、この反論を満足させていると考える。

我々の理論が実際的な予測をするための助けとして、確率論的解釈の使用を最終的に正当化するが、それはその解釈の一貫性を理解するためのより広い枠組みを形成する。この点で、それは標準理論のためのメタ理論を形成すると言える。しかし、それは通常の「外部観測」の定式化を超越しているが、不完全な観測と近似測定の問題に論理的に対処できる。

「相対状態」の定式化は、重ね合わせの原理を維持するすべての形式の量子力学に適用される。それゆえ、それは一般相対論の量子化のための実りある枠組みを証明するかもしれない。形式主義は、最初に形式理論を構築し、後で統計的解釈を提供するように促す。この方法は、観測者と対象系を分離することに疑問がない場合に、量子化された統一場の理論を解釈するのに特に役立つ。それらはすべて単一の構造体である場で表現される。どんな解釈規則もおそらく理論自体の中でそして理論を通してのみ推論できる。

理論の実際的な利点とは別に、通常の解釈の統計的主張は独立した仮説の地位を持たないが、統計的仮説から完全に解放されている純粋な波動力学から(現在の意味では)推論できたことは、依然として知的な関心事である。