量子力学の確率解釈では、ある電子の波動関数は、その電子の観測確率をあらわすと解釈します。 量子力学の確率解釈はボルンの規則ともよばれます。ボルンの規則とは、電子のような小さな粒子の観測確率は、 その粒子の波動関数の絶対値の二乗に比例するという規則です。 このページでは、ボルンの規則の導出方法を紹介します。
一般的にボルンの規則は、量子力学の基本原理だと考えられています。 基本原理とは、それ以上問うことのできない前提であることを意味します。 そのため、多くの人は、ボルンの規則を、別の基本原理から導出しようとは考えません。 では、なぜ私はボルンの規則を、別の基本原理から導出しようとしているのでしょうか?
それは、私が「ボルンの規則は基本原理だろうか?」という疑問をもっているからです。 ボルンの規則によれば、電子の観測確率は、波動関数の絶対値の二乗に比例します。 私は、ボルンの規則を基本原理とは考えません。なぜなら、私は確率をラプラスの確率論で計算すべきと考えるからです。 ラプラスの確率論は次節で説明します。
ラプラスの確率論とは、確率を計算するための理論です。 フランスの数学者ピエール=シモン・ラプラスが1814年に、その理論を提案しました。 たとえば、袋の中に赤い球が3個、青い球が2個入っているとします。

その袋の中に手を入れて、球を取り出します。赤の球を取り出す確率はいくらでしょうか? この確率はラプラスの確率論で計算できます。 ラプラスの確率論では、事象と素事象という概念を使います。事象とは出来事のことです。 素事象とは、それ以上分けることのできない事象のことです。 たとえば、赤い球を取り出すという事象Rは、次の三種類の事象に分けることができます。
「球r-1を取り出す事象」はそれ以上分けることができないため、素事象です。 ラプラスの確率論では、期待する素事象の個数を、すべての素事象の個数で割ることで、確率を計算します。 たとえば、赤い球を取り出す事象Rの確率は、3/5です。 なぜならば、期待する素事象の個数は3であり、すべての素事象の個数は5だからです。
ボルンの規則にもとづく確率の計算方法は、 ラプラスの確率論にもとづく計算方法と、まったく異なります。 ラプラスの確率論では、確率を素事象の個数の比で計算するのに、 なぜ、ボルンの規則では、確率は波動関数の絶対値の二乗で計算するのでしょうか? このページでは、この疑問を「量子力学の確率問題」と呼ぶことにします。 この頁では、多世界解釈と確率論で、この確率問題の解法を考えます。 次の節では多世界解釈について説明します。
多世界解釈では、世界のすべてを波動関数で表現します。 この「世界のすべてを表現する波動関数」に対する描像が、個人によって大きく異なります。 宇宙の波動関数を想像するには、一個の粒子の波動関数から始め、 徐々にその個数を増やしていく必要があります。
確率問題を考えるため、多粒子の波動関数を考えます。
k番目の素粒子の位置を \begin{align*} r_k=(x_k,y_k,z_k), \end{align*} とすると多粒子の波動関数は次のようになります。
\begin{align*} \Psi=\Psi(r_1,r_2,r_3,\cdots,r_n) \end{align*}この波動関数は、n 個の素粒子の位置を表現しています。 素粒子の配置を変えれば、あらゆる宇宙を構成できます。
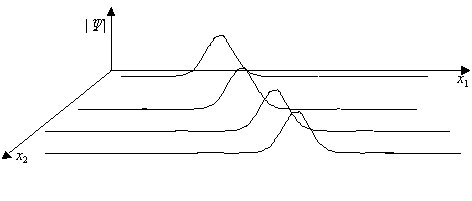
多粒子の波動関数の一点が、一つの世界に対応します。 その確率分布P は次のようになります。
\begin{align*} P(r_1,r_2,r_3,\cdots,r_n)=|\Psi(r_1,r_2,r_3,\cdots,r_n)|^2 \end{align*}次の論文は、ボルンの規則を多世界解釈と確率論で導出します。
多世界解釈でボルンの規則を導出する際に、必要となった概念が次の階層宇宙という概念です。 階層宇宙の詳細は論文を参照願います。
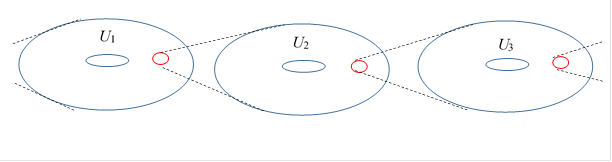
ここでは、階層宇宙の概略を説明しようと思います。
階層宇宙とは入れ子になった宇宙です。
我々の宇宙には粒子が存在します。そしてその粒子に対応する波動関数が存在します。 その波動関数の絶対値を半径とする小さな別の宇宙が存在すると考えます。
その小さな宇宙には粒子が存在します。そしてその粒子に対応する波動関数が存在します。 その波動関数の絶対値を半径とする、さらに小さな別の宇宙が存在すると考えます。
また、我々の宇宙の半径を絶対値とする波動関数が存在します。 その波動関数に対応する粒子が存在します。その粒子は、大きな別の宇宙に存在します。
つまり我々の宇宙と小さな宇宙は波動関数によって結ばれているのです。
© 2012-2013 xseek-qm.net
広告


