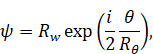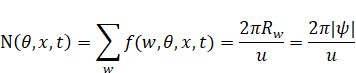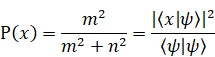波動関数の幾何学的解釈による量子確率
2019/02/17
公開日 1999/11/21[1]
K. Sugiyama[2]
量子論の確率的な予測は不思議な現象である。本論文は波動関数を幾何学的に解釈することで、この不思議な現象を解明する。
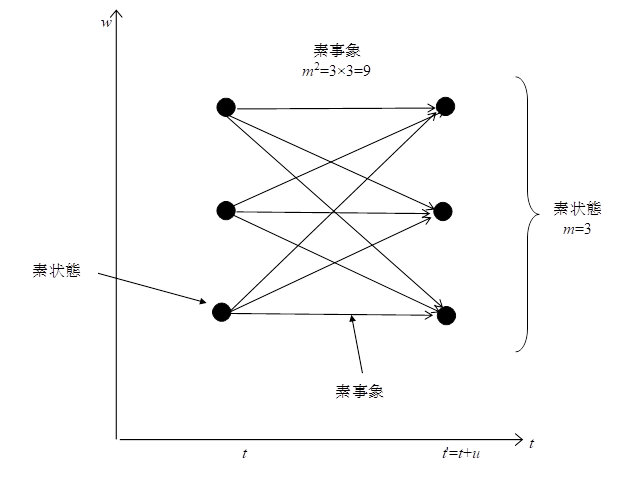
図 4-1: 素事象の本数は素状態の個数の2乗
この結果は量子論と相対論の統一の可能性を示唆する。また、この結果は多世界解釈の妥当性を示唆する。
目次
1 序論
量子論の確率的な予測を提供する多世界解釈の理論は存在しない[3]。量子論の確率的な予測を得るため、いくつかの仮説を立て、多世界解釈のための理論を構築する。その理論を多事象理論と呼ぶ。
2 仮説
2.1 「無境界」仮説
位置x、時刻t、位相θのような物理量がいくつか存在している。これらの物理量を「位置的量」と呼ぶ。すべての位置的量は境界を持たず、有界閉集合と仮定する。
2.2 「最小単位」仮説
すべての位置的量は共通の最小単位uを持つと仮定する。
2.3 「波動空間」仮説
新しいもう一つの位置的量wを仮定する。その量の空間を波動空間と呼ぶ。この量は波動関数と関係する。
2.4 「位相空間」仮説
メビウスの帯のような構造を持つ位相空間θ を仮定する。これは波動関数のスピンとの類似である。したがって、波動関数を次のように定義する。
|
|
(2.1) |
ここで、Rwは波動空間の曲率半径である。また、Rθ は位相空間の曲率半径である。Rw、 Rθ と θは、変数θ、xと tの関数である。
2.5 「素状態」仮説
状態の最小単位を仮定する。この状態を素状態と呼ぶ。例えば、量子論における一個の粒子の素状態を次のように表現する。
|
|
(2.2) |
素状態は位置的量の組み合わせで指定できる。同一の素状態は、ただひとつだけであると仮定する。したがって、素状態は空間内の一点と解釈できる。ある一つの状態は、それらの点の集合と対応する。
2.6 「素事象」仮説
ある一つの素状態から別のもう一つの素状態への遷移を素事象と呼ぶ。同一の素事象は、ただ一つだけであると仮定する。したがって、したがって、素事象は空間内の一本の線と解釈できる。ある一つの事象は、それらの線の集合と対応する。
すべての可能な素事象は存在する。これは経路積分との類似である。
3 円環の構成
問題を簡単にするため、一個の粒子を考えよう。そして、w, θ ,x ,t を使用する。次のように円環を構成する。
|
|
(3.1) |
そして、円環の表面上にある一点を次のように定義する。
|
|
(3.2) |
Rw は波動関数のように、近似的な線形性を持つ。もしも円環の表面上に波が存在した場合、位相空間内における一周の効果と、二周の効果は相殺する。なぜならば、位相空間がメビウスの帯のような構造を持つからである。したがって、Rwは波動関数のような性質を持つ。
円環の形状は、その系のハミルトニアンHによって決定される。多数の粒子を記述するには、新しい位置的量を必要とする。これは第二量子化の類似である。
円環の表面上の一点は素状態f (w, θ, x, t)である。位置的量は最小単位を持つため、素状態は数えることができる。素状態の個数N (θ, x, t)を次のように計算する。
|
|
(3.3) |
ここで、u は最小単位であり、f (w, θ, x, t) = 1である。
4 確率
量子論の確率とは、ある一つの事象の確率である。異なる素事象の個数だけを考察すればよい。なぜならば、我々は、多くの素事象のうちの、たった一つの素事象だけを観測するからである。
ここで、次の式を仮定する。
|
|
(4.1) |
また、次の式を仮定する。
|
|
(4.2) |
このとき、素状態の異なる組み合わせの個数としてm2を得る。なぜならば、時間が最小単位を持つからである。それらの組み合わせとは、素事象のことである。もしも、m個の異なる素状態が存在するならば、m2個の異なる素事象が存在する。
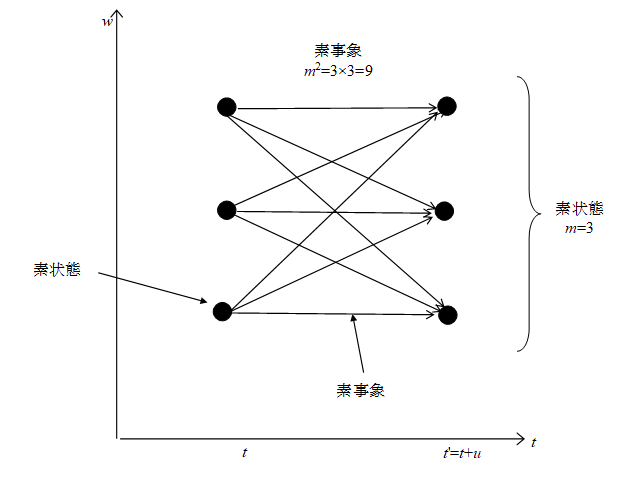
図 4-1: 素事象の本数は素状態の個数の2乗
もしも、状態 
が存在するならば、位置xである一個の粒子を発見する確率P (x) は次のように表現できる。
|
|
(4.3) |
したがって、この理論から確率を得ることができる。個々の素事象は存在する。したがって、個々の素事象を観測する観測者も存在する。この帰結は、多世界解釈である。
5 結論
この理論は量子論の確率を提供する。
6 参考文献
