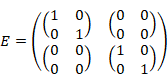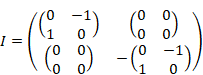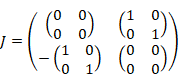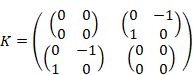3次元球面の回転によるスピン1/2の二価性と角運動量の導出

 

ホーム > 量子力学 > 量子力学のスピン

 

2022/05/25

公開日 2013/05/19

K. Sugiyama^[1]

 

本論文では、3次元球面の回転でスピン1/2の二価性と角運動量を導出する。

 

 

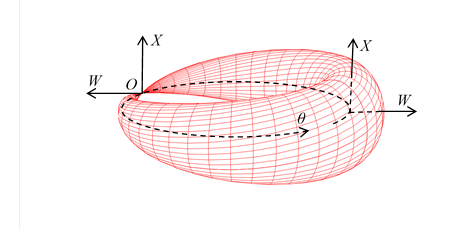
図 3‑8: スピン1/2の粒子の波動関数

 

スピンの波動関数は360度回転で、その符号を変える。そのため、もし角度の依存するスピン1/2の波動関数が存在すると仮定するならば、角度0度および360度において波動関数は二種類の値を取る。この奇妙な振舞いは「スピン1/2の二価性」と呼ばれている。この「スピンの二価性」により、角度に依存するスピン1/2の波動関数は存在しないと考えられている。

 

この「スピン1/2の二価性」の謎を解決するには、波動関数の概念を変革する必要がある。かつてカルツァとクラインは電磁場の関数を一次元の円と解釈した。それと同様に、本論文は波動関数を3次元球面と解釈する。

 

この三次元球面を次のように分解する。

上記の式のW-X平面の円を図 3‑8に示している。角度θが360度回転すると、この円は裏返る。この性質が「スピン1/2の二価性」の正体である。

 

目次

1      序論... 1

1.1       課題... 1

1.2       課題の重要性... 1

1.3       研究の経緯... 1

1.3.1        スピンの研究の経緯... 1

1.3.2        多様体の研究の経緯... 1

1.4       本論文の新しい構成方法... 1

2      これまでのスピンの研究結果の確認... 1

2.1       パウリ行列と四元数... 1

2.2       スピンの二価性と角運動量の実験の確認... 1

2.2.1        スピンの二価性の実験による検証... 1

2.2.2        スピンの角運動量の実験による検証... 1

3      スピンの二価性と角運動量の導出... 1

3.1       スピンの二価性の導出... 1

3.1.1        三次元球面の考察... 1

3.1.2        同時断面法による二次元球面の観察... 1

3.1.3        同時断面法による三次元球面の観察... 1

3.1.4        同時断面法による三次元球面の観察(別の方法) 1

3.1.5        偶円環と奇円環... 1

3.2       スピンの角運動量の導出... 1

3.2.1        一次元の螺旋空間の構成... 1

3.2.2        二次元の螺旋空間の構成... 1

3.2.3        三次元の螺旋空間の構成... 1

3.2.4        三次元の螺旋空間の考察... 1

4      結論... 1

5      今後の課題... 1

6      補足... 1

6.1       三次元球面のスピン... 1

7      付録... 1

7.1       用語整理... 1

8      謝辞... 1

9      参考文献... 1

 

 

 

1    序論

1.1  課題

カルツァとクラインは、重力と電磁気力を統一するために、余剰次元空間にある一次元球面を導入した。本論文では、スピン1/2の二価性と角運動量を導出するために、余剰次元空間にある三次元球面を導入する。

 

1.2  課題の重要性

多くの研究者が、重力の量子化を試みてきたが、成功には至っていない。この重力の量子化は物理学の重要な課題となっている。重力を量子化する方法の一つは、点粒子を一次元多様体である弦と解釈する方法だった。従って、スピンの波動関数を多様体と解釈することは、重力の量子化に有効であると推測できる。

 

1.3  研究の経緯

1.3.1 スピンの研究の経緯

ウーレンベックとゴーズミットは、1925年に電子のスピン(自転)を発見した。パウリは、1927年にパウリ行列でスピンを定式化した。ディラックは、1928年にディラック方程式でスピンを導出した。

 

1.3.2 多様体の研究の経緯

アインシュタインは、1916年に四次元リーマン多様体で一般相対性理論を構成した。カルツァ^[2]とクライン^[3]は、1926年に一次元の円で、カルツァ=クライン理論を構成した。

 

1.4  本論文の新しい構成方法

スピン1/2の波動関数を三次元球面と解釈する。この三次元球面を二つの円に分解し、回転させることで、スピン1/2の二価性を表現する。

 

2    これまでのスピンの研究結果の確認

2.1  パウリ行列と四元数

パウリはスピンを表現するため、1927年に次のパウリ行列を定義した。

積は次のとおり。

 

このパウリ行列で単位四元数を定義する。

(単位四元数)

積は次のとおり。

これは次の単位四元数の行列表現である。

単位四元数は、ウィリアム・ローワン・ハミルトンが1843年に発見した。

 

2.2  スピンの二価性と角運動量の実験の確認

2.2.1 スピンの二価性の実験による検証

ラウチ^[4]とウェルナー^[5]が1975年に中性子干渉法による実験でスピンの二価性を検証した。本節では、スピンの二価性を確認する。

 

z軸周りで回転している粒子の波動関数はパウリ行列で次のように表現できる。

回転角度θを360度回転すると、位相は同じ状態に戻らず、反対の位相の状態となる。回転角度θを720度回転すると、元の状態に戻る。

 

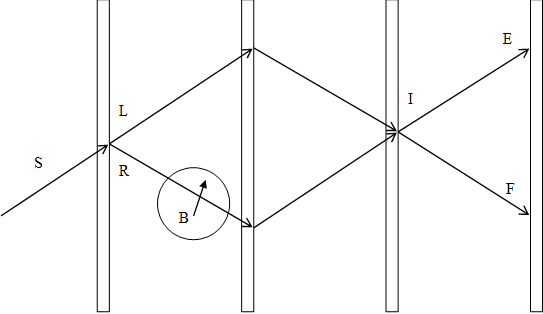
図 2‑1: スピンの二価性を検証する実験

 

中性子を経路 L と経路 R に分割する。経路 L の中性子は磁場のない領域を通る。経路 Rの中性子は磁場のある領域を通る。その結果、磁場は経路 R を通る中性子の位相を変化させる。位相の変化量  は次のとおり。

ここで、変数 ω は中性子のスピンの歳差運動の角振動数である。変数 T は中性子が磁場を通過する時間である。変数 g_n は中性子のg因子である。定数 e は素電荷である。変数Bは磁場の強さである。変数 m は中性子の質量である。

 

経路 L と経路 R を通った中性子は位置 I で合流する。中性子は位置 E または位置 F で観測できる。

位置 E または位置 F では波動関数の重ね合わせが発生するため、位相変化を観測できる。実験の結果、この位相変化が実際に観測された。

この実験によりスピンが二価性を持つことが明らかとなった。

 

2.2.2 スピンの角運動量の実験による検証

アインシュタインとドハース^[6]は1915年に、次のような実験で、スピンの角運動量を検証した。

 

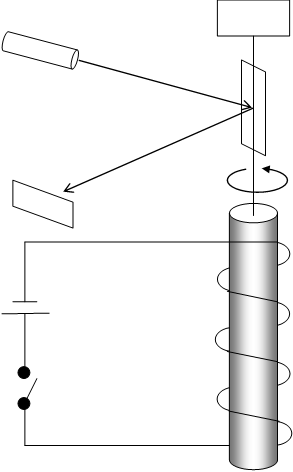
図 2‑2: スピンの角運動量を検証する実験

 

実験は次のように行われた。

磁性体の円盤に磁場をかける。そして、円盤を静止状態にする。その後、磁場をとめる。すると円盤は回り始める。この効果はアインシュタイン＝ドハース効果と呼ばれている。この実験によって、スピンが角運動量を持つことが明らかとなった。

 

3    スピンの二価性と角運動量の導出

3.1  スピンの二価性の導出

点粒子の回転半径は零のため、点粒子は回転できない。回転半径、零で有限の角運動量を得るには、無限大の運動量が必要となる。

角運動量 L は半径 r と運動量 p で次のように表現できる。演算子 × は外積である。

 

 

角運動量 L が有限で、半径 r が零ならば、運動量 p は無限大となる。

 

一方、二次元球面の回転ではスピンの二価性を導出できない。そこで、三次元球面の回転を考察する。

 

 

3.1.1 三次元球面の考察

三次元球面 S³ は、次の図の2個の三次元球体 B³ の表面を張り合わせることで表現できる。

図 3‑1: 三次元球面

 

次の図に示すように、三次元球面には、 R₁, R₂, R₃, R₄, R₅, R₆ の6種類の自転がある。

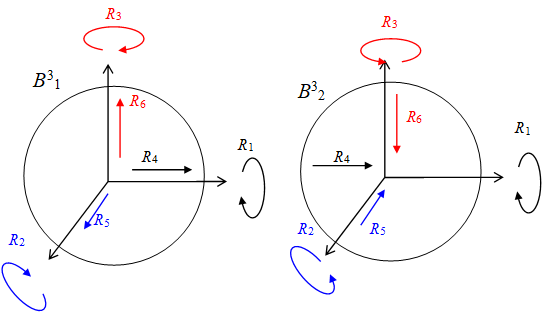
図 3‑2: 三次元球面の回転

 

自転 R₁, R₂, R₃ の考察は困難でない。しかし、自転 R₄, R₅, R₆ の考察は困難である。

 

三次元球面は四次元空間に存在するため、考察困難である。そこで、三次元球面の2枚の断面図を同時に見ることで、三次元球面の考察を試みる。

このように2枚の断面図を同時に見る手法を同時断面法と呼ぶこととする。

 

最初に、二次元球面に同時断面法を適用する。なぜなら、二次元球面は三次元球面よりも考察が容易なためである。

 

3.1.2 同時断面法による二次元球面の観察

座標(X, Y, Z) で指定される余剰三次元空間に二次元球面S²があると仮定する。二次元球面の半径を1とすると、二次元球面は次の式を満たす。

この球面は、X-Y 平面の断面図と、Z軸上の位置で表現できる。

 

ここで、角度θは次の式を満たす。

同時断面法を適用した二次元球面を次の図に示す。

 

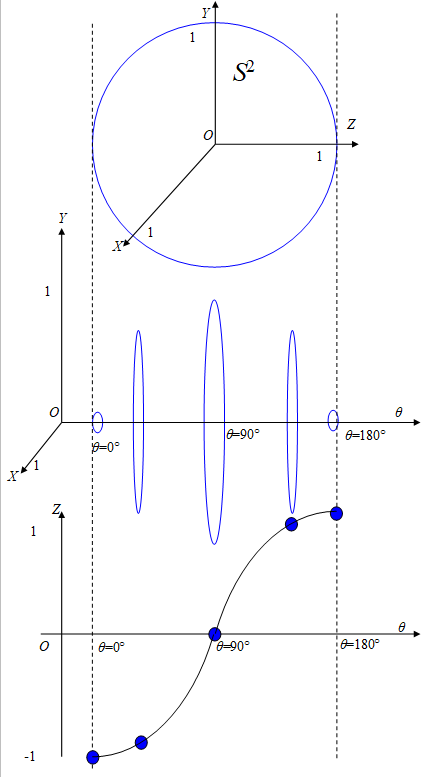
図 3‑3: 二次元球面の同時断面図

 

角度θでのX-Y 平面の円の半径と位置Zを次の表に示す。

 

表 3-1: 角度θでのX-Y平面の円の半径と位置Z

 

このように、X-Y平面の円の半径と位置Zを同時に観察することにより、二次元球面の構造を考察できる。

 

次に同時断面法を三次元球面に適用する。

 

3.1.3 同時断面法による三次元球面の観察

座標(W,X,Y,Z)で指定される余剰四次元空間に三次元球面S³があると仮定する。球面の半径を1とすると、三次元球面は次の式を満たす。

 

この球面について、X-Y-Z空間の断面図と、W軸上の位置で表現する。

同時断面法を適用した三次元球面を次の図に示す。

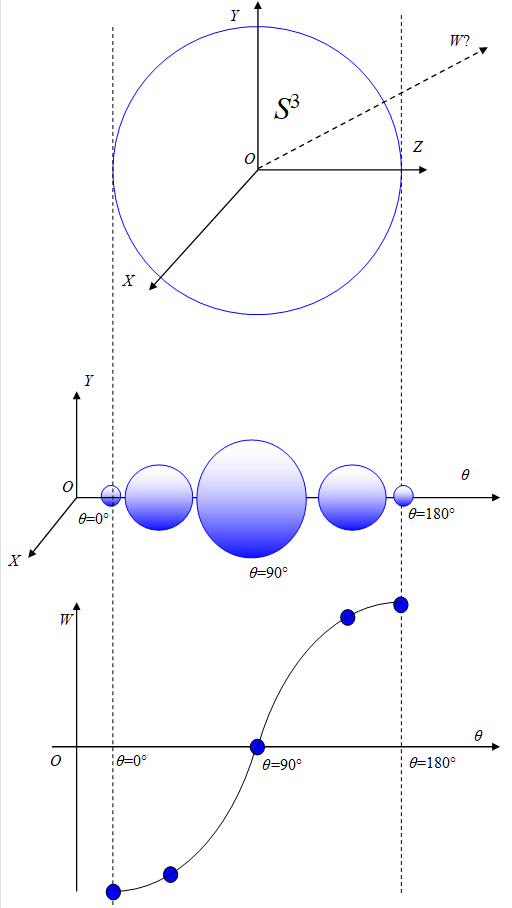
図 3‑4: 三次元球面の同時断面図

 

角度θでのX-Y-Z空間の球面の半径と位置Zを次の表に示す。

 

表 3-2: 角度θでのX-Y-Z空間の球面の半径と位置Z

 

本節では、三次元球面を二次元球面と軸上の位置に分けた。しかし、三次元球面を別の方法で分けることもできる。その方法を次節で考察する。

 

3.1.4 同時断面法による三次元球面の観察(別の方法)

座標 (W,X,Y,Z) で指定される余剰四次元空間に三次元球面S³があると仮定する。球面の半径を1とすると、三次元球面は次の式を満たす。

この球面について、W-X平面の断面図と、Y-Z平面の断面図で表現する。

これはハインツ・ホップが1931年に発見したホップ・ファイブレーションである。

同時断面法を適用した三次元球面を次の図に示す。

 

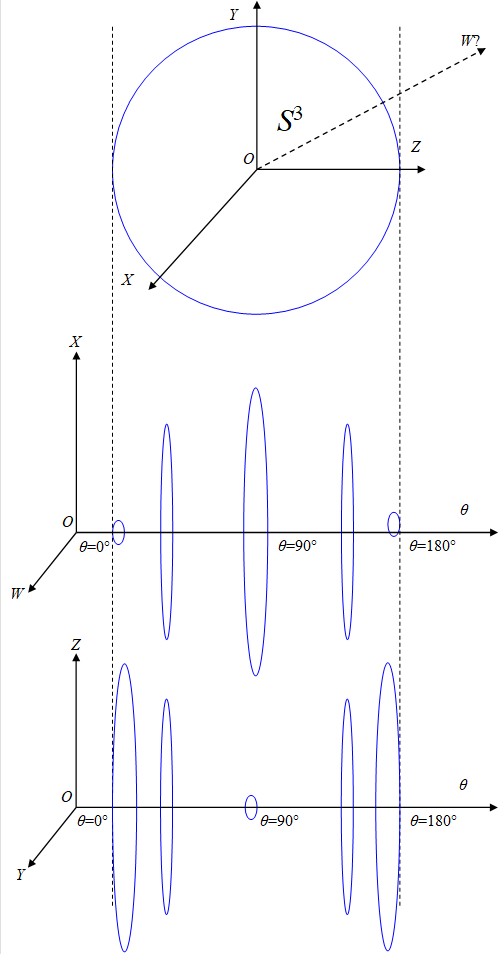
図 3‑5: 三次元球面の同時断面図 (別の方法)

 

 

角度θでのW-X平面の円の半径とY-Z平面の円の半径を次の表に示す。

 

表 3-3: 角度θでのW-X平面の円の半径とY-Z平面の円の半径

 

ここで、角度θ = 0° のW-X平面の円と、角度θ = 180° のW-X平面の円を接続できる。なぜならそれらは同じ半径0を持つからである。さらに、角度θ = 0° のY-Z平面の円と、角度θ = 180° のY-Z平面の円も接続できる。なぜならそれらは同じ半径1を持つからである。

 

したがって、角度θは多様体の回転角度と解釈できる。

 

この回転は、円を裏返す。たとえば、Y-Z平面の円は回転角度θ = 180°で裏返る。そのため、この回転は、通常の自転とは異なる奇妙な自転である。

 

この奇妙なスピンを「円環自転(円転)」と呼ぶこととする。また通常の自転を「球面自転(球転)」と呼ぶこととする。

 

 

3.1.5 偶円環と奇円環

ここで、三次元球面を次のように表現する。

この三次元球面は、同時断面法により、次の図で表現できる。

 

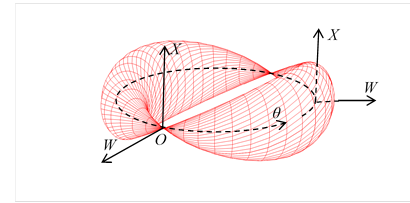
図 3‑6: スピン1の粒子の波動関数(W-X-θ)

 

 

 

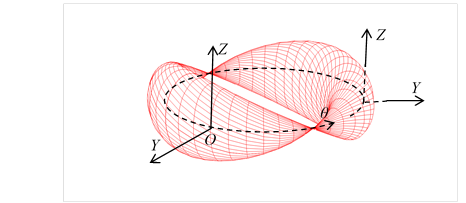
図 3‑7: スピン1の粒子の波動関数(Y-Z-θ)

 

 

 

上記の円環はスピン1の粒子の波動関数と解釈できる。複素関数で次のように表現できる。

 

 

 

次に、三次元球面を次のように表現する。

この三次元球面は、同時断面法により、次の図で表現できる。

図 3‑8: スピン1/2の粒子の波動関数(W-X-θ)

 

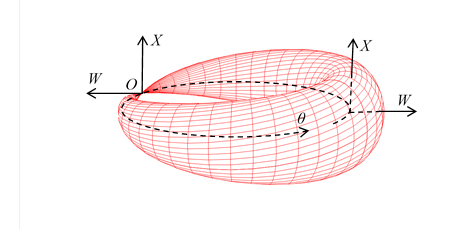
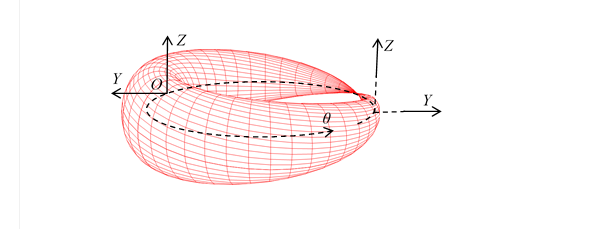
図 3‑9: スピン1/2の粒子の波動関数(Y-Z-θ)

 

 

上記の円環はスピン1/2の粒子の波動関数と解釈できる。複素関数で次のように表現できる。

 

 

ここで、三次元球面を次のように表現する。

変数nは整数である。偶数nの円環を偶円環と呼ぶこととする。また、奇数nの円環を奇円環と呼ぶこととする。

 

3.2  スピンの角運動量の導出

本論文で、スピンを三次元球面の回転と解釈した。なぜ、三次元球面の回転が、通常の三次元空間の角運動量と同じ角運動量を持つのだろうか？

 

本節では、三次元球面が通常の三次元空間とつながっている可能性を考察する。

 

3.2.1 一次元の螺旋空間の構成

一次元の螺旋空間は次のように構成できる。

 

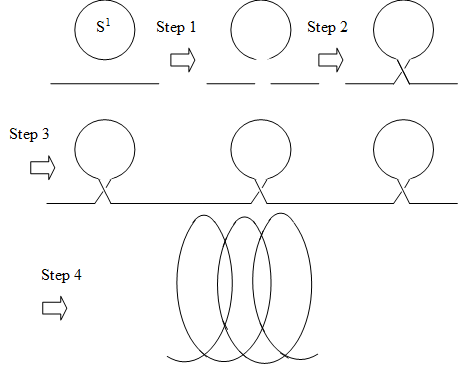
図 3‑10: 一次元螺旋空間の構成

 

図の各ステップでの変換を次の表で説明する。

 

表 3-4: 一次元螺旋空間の構成

 

 

一次元の螺旋空間は複素数の行列表現で次のように表現できる。

 

変数 W,X は余剰空間の座標である。変数 R は余剰空間の半径である。変数 Θ は余剰空間内の角度である。

 

記号 {E, I} は複素数の行列表現である。

通常空間の座標 x は波長 λ で次のように表現できる。

 

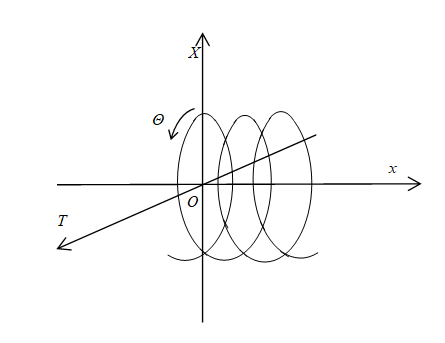
図 3‑11: 一次元螺旋空間

 

さらに、両端を結合すれば、一次元螺旋円を構成できる。

ここで、 n は整数である。変数Θは、螺旋円の大円の回転角である。変数 rは、螺旋円の大円の半径である。変数 Rは、螺旋円の小円の半径である。変数 {W, X} は余剰空間の座標である。変数 x は通常空間の座標である。

 

この一次元螺旋円は、次の図で表現できる。

 

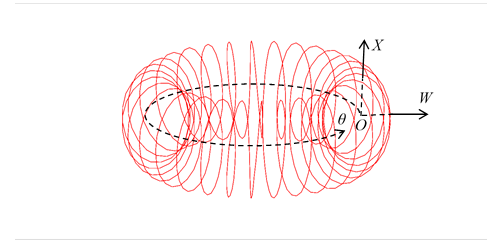
図 3‑12: 一次元螺旋円

 

これと同じことを二次元でも実施できるだろうか？それを次の節で考察する。

 

3.2.2 二次元の螺旋空間の構成

二次元の螺旋空間は次のように構成できる。

 

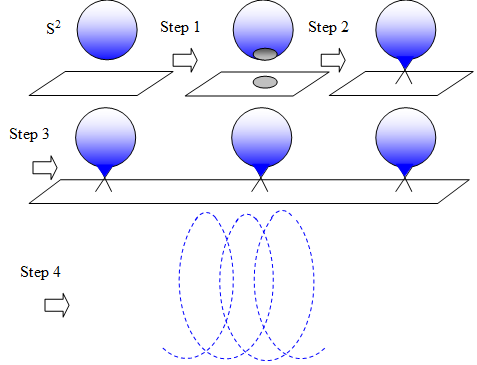
図 3-13: 二次元螺旋空間

 

図の各ステップでの変換を次の表で説明する。

 

表 3-5: 二次元螺旋空間の構成

 

 

二次元の螺旋空間は三角関数で表現できない。また、二次元の螺旋空間は複素数で表現できない。そのため、二次元の螺旋空間は存在しないと推測する。しかし、三次元の螺旋空間は存在する可能性がある。それを次の節で考察する。

 

3.2.3 三次元の螺旋空間の構成

三次元の螺旋空間は次のように構成できる。

 

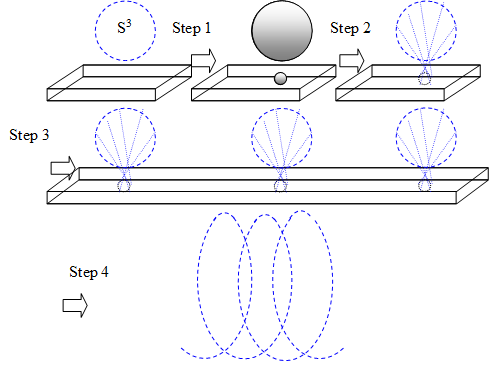
図 3‑14: 三次元螺旋空間

 

図の各ステップでの変換を次の表で説明する。

 

表 3-6: 三次元螺旋空間の構成

 

三次元の螺旋空間は単位四元数の行列表現{E, I, J, K} で次のように表現できる。

変数 {W, X, Y, Z } は余剰空間の座標である。{Θ₁, Θ₂, Θ₃}  は余剰空間内の角度である。Rは余剰空間の半径である。

 

単位四元数の行列表現{E, I, J, K}は次の通り。

 

通常空間の座標 (x, y, z) は波長 {λ₁, λ₂, λ₃} で次のように表現できる。

 

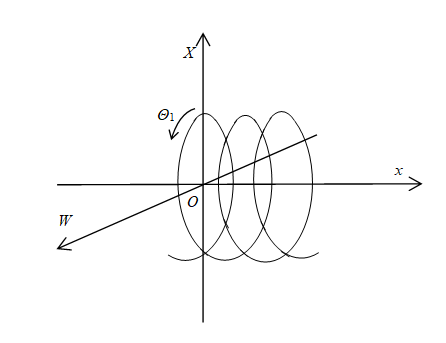
図 3-15: 三次元螺旋空間

 

さらに、両端を結合すれば、三次元螺旋球面を構成できる。

 

ここで、{n_1, n_2, n₃} は整数である。{Θ₁, Θ₂, Θ₃} は、螺旋円の大円の回転角である。変数rは、螺旋円の大円の半径である。変数Rは、螺旋円の小円の半径である。変数 {x, y, z} は通常空間の座標である。

 

この三次元螺旋球面は、象徴的に、次の図で表現できる。

 

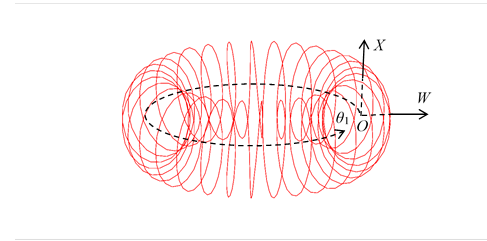
図 3-16: 三次元螺旋球面

 

 

3.2.4 三次元の螺旋空間の考察

一次元螺旋空間には複素数が対応した。一方、三次元螺旋空間には四元数が対応した。三元数が存在しないため、二次元螺旋空間は存在しないと推測する。

 

三次元螺旋空間内の位置は通常の三次元空間内の座標と解釈できる。従って、三次元球面の角運動量は、通常の三次元空間内の角運動量と解釈できる。別の言葉で言えば、量子力学のスピンは粒子の回転と解釈できる。

 

4    結論

本論文で、スピンの次の性質を導出した。

(1) スピンの二価性

(2) スピンの角運動量

 

5    今後の課題

今後の課題は次のとおり。

(1)   ディラック方程式の導出

 

 

 

6    補足

6.1  三次元球面のスピン

本論文は、三次元空間の波動関数として三次元球面を導入した。

その三次元球面を四元数関数で次のように表現する。

これはホップ・ファイブレーションである。

角度 θ に対する座標 (W, X ) を次の図に示す。

 

 

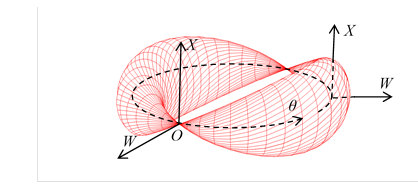
図 6-1: スピン1の粒子の波動関数

 

回転角度が180度の四元数関数fの値は、

回転角度が0度の四元数関数fの値の(-1)倍となる。

回転角度が360度の四元数関数fの値は、

回転角度が0度の四元数関数fと同じ値になる。

この多様体をスピン1の粒子の波動関数と解釈する。

この多様体の回転角度を波動関数の位相と解釈する。

この多様体の表面積を波動関数の絶対値と解釈する。

 

 

ここで、角度 θ を半分の角度に変更にする。

 

すると、四元数関数は次のように表現できる。

 

回転角度 θ に対する座標 (W, X ) を次の図に示す。

 

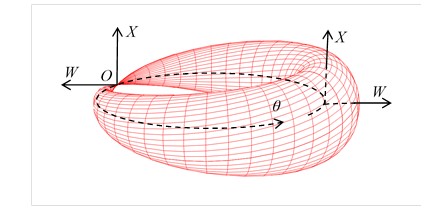
図 6-2: スピン1/2の粒子の波動関数

 

 

回転角度が360度の四元数関数fの値は、

回転角度が0度の四元数関数fの値の(-1)倍となる。

回転角度が720度の四元数関数fの値は、

回転角度が0度の四元数関数fと同じ値になる。

この多様体をスピン1/2の粒子の波動関数と解釈する。

この多様体の回転角度を波動関数の位相と解釈する。

この多様体の表面積を波動関数の絶対値と解釈する。

 

7    付録

7.1  用語整理

 

表 7-1: 自転等

 

表 7-2: 螺旋空間等

 

8    謝辞

本論文を作成するにあたり、貴重な助言を頂いたNS氏に心より感謝いたします。

9    参考文献

10