In simple terms, Bell’s inequality sets an upper bound on the probability that Alice and Bob will meet.
This article explains Bell’s inequality clearly and accessibly.
Bell’s inequality is written as follows:
If this differs from the version of Bell’s inequality you are familiar with, see "Various Bell’s Inequalities" below.
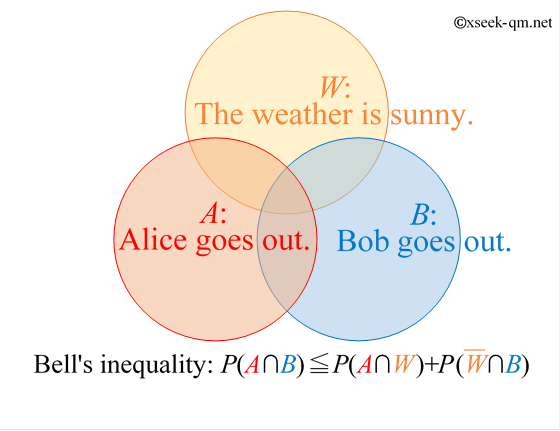
To make it more concrete, the symbols $W$, $A$, and $B$ are replaced with everyday terms:
Here, $P(A \cap B)$ is the probability that Alice and Bob go out together. $P(A \cap W)$ is the probability that it is sunny and Alice goes out. $P(\overline{W} \cap B)$ is the probability that it is rainy and Bob goes out ($\overline{W}$ denotes rain).
In these terms, Bell’s inequality reads:
The possible scenarios are as follows:
We can illustrate these cases with a Venn diagram:

The following figure makes it even clearer that Bell’s inequality is satisfied.
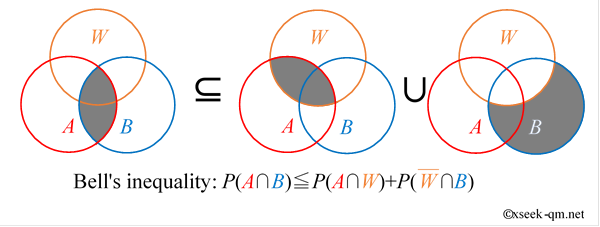
This visual representation is Bell’s inequality. It shows how the inequality works in terms of overlapping probabilities.
Consider this scenario:
In this context, Bell’s inequality becomes:
With that in mind, consider the following problem:
Under these conditions, what is the maximum possible probability in percent that Alice and Bob meet?
The answer is 25%. Here is the reasoning.
First, note that the question asks for the maximum meeting probability.
We break the calculation into sunny and rainy days. Starting with sunny days:
The probability of a sunny day is 50%, and Alice goes out on sunny days with probability 25%. Therefore, the probability $P(A \cap W)$ that it is sunny and Alice goes out is 50% × 25% = 12.5%.
On the other hand, Bob goes out on sunny days with probability 75%, so the probability $P(B \cap W)$ that it is sunny and Bob goes out is 50% × 75% = 37.5%.
For Alice and Bob to meet on a sunny day, both must go out. Hence the maximum probability that they meet on a sunny day is the smaller of the two “sunny and going out” probabilities $P(A \cap W)$ — namely, 12.5%.
The probability of rain is 50%, and on rainy days Alice goes out with probability 75%. Therefore, the probability $P(\overline{W} \cap A)$ that it is raining and Alice goes out is 50% × 75% = 37.5%.
On the other hand, Bob goes out on rainy days with probability 25%, so the probability $P(\overline{W} \cap B)$ that it is raining and Bob goes out is 50% × 25% = 12.5%.
For Alice and Bob to meet on a rainy day, both must go out. Hence the maximum probability that they meet while it is raining is the smaller of the two “rain and going out” probabilities $P(\overline{W} \cap B)$ — namely, 12.5%.
Combining the maximum probability of meeting on a sunny day (12.5%) and the maximum probability of meeting on a rainy day (12.5%), we find that the maximum probability of meeting is 25%.
Therefore, Bell's inequality in this problem is as follows:
Thus, the answer to the question "What is the maximum possible probability that Alice and Bob meet?" is 25%. As long as the conditions of this problem are met, regardless of how the calculation is done, it is impossible to obtain a higher probability. This conclusion should always be correct as long as the weather can be clearly divided into sunny and rainy days. However, surprisingly, in the world of quantum mechanics, the left side of this inequality ($P(A \cap B)$) can be 37.5%! I explain this next.
Consider the following thought experiment based on quantum mechanics:
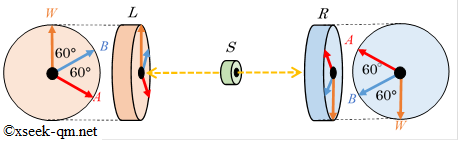
The central source $S$ emits one electron to the left observation device $L$ and another electron to the right observation device $R$. These two electrons are in a special relationship (EPR pair), generated, for example, such that their total spin is 0.
The observation devices can measure the electron's spin in a specified direction. A strange aspect of quantum mechanics is that when measured, an electron's spin always takes a value of either $+1/2$ or $-1/2$. If the total spin is 0, and the left observation device $L$ observes spin $+1/2$ in direction $W$, then if the right observation device $R$ measures the spin in the same direction $W$, it will always observe the opposite spin $-1/2$. (The original text says "measuring in the same direction gives the same result 100%", but for an EPR pair with total spin 0, opposite correlations are typically observed. Here, we proceed with the text's premise of "same result" for the sake of argument, but the physical setup might imply a different interpretation. We interpret $P(A \cap B)$ as "the probability of observing +1/2 on both sides.")
From here, the explanation becomes more complex. The left observation device $L$ measures the spin of one electron in direction $A$. Meanwhile, the right observation device $R$ measures the spin of the other electron in direction $B$. Let the angle between direction $A$ and direction $B$ be $\theta$. According to quantum mechanics, the conditional probability that the right device $R$ observes $+1/2$ in direction $B$, given that the left device $L$ observed $+1/2$ in direction $A$, can be calculated by the following formula:
$$ P(B|A) = \frac{ P(A \cap B)}{P(A)}= \cos^2 \left(\frac{\theta}{2} \right) $$ (Note: This formula represents the probability for a specific setup. Often, for EPR pairs, it's $\sin^2(\theta/2)$, but we follow the text's formula here.)Here, $P(B|A)$ is the probability that event $B$ (right observes +1/2) occurs given that event $A$ (left observes +1/2) occurred. $P(A \cap B)$ is the probability that events $A$ and $B$ occur simultaneously. $P(A)$ is the probability of observing +1/2 on the left, which is usually 1/2 (50%). Here are some examples:
As the setup for the thought experiment, let's set direction $W$ as the reference (0°), direction $A$ as 120°, and direction $B$ as 60°. (This differs from the original problem setup but uses angles commonly used to demonstrate the inequality violation. We adjust angles according to the original text's diagram). In the original text's diagram, it seems the angle between $A$ and $W$, and between $\overline{W}$ and $B$ is 120°, and the angle between $A$ and $B$ is 60°.
First, let's calculate the joint probability $P(A \cap B)$. The angle difference is $60^\circ$, so,
$$ P(B|A) = \cos^2 \left(\frac{60^\circ}{2} \right) = \cos^2(30^\circ) = (\sqrt{3}/2)^2 = 3/4 = 75\% $$Since $P(A)=1/2$, the probability $P(A \cap B)$ that both measurement devices simultaneously obtain electron spin $+1/2$ is $P(A \cap B) = P(A) \times P(B|A) = (1/2) \times 75\% = 37.5\%$.
$$ P(A \cap B) = 37.5\% $$Next, let's calculate the joint probability $P(A \cap W)$. The angle difference is $120^\circ$, so,
$$ P(W|A) = \cos^2 \left(\frac{120^\circ}{2} \right) = \cos^2(60^\circ) = (1/2)^2 = 1/4 = 25\% $$Since $P(A)=1/2$, the probability $P(A \cap W)$ that both measurement devices simultaneously obtain electron spin $+1/2$ is $P(A \cap W) = P(A) \times P(W|A) = (1/2) \times 25\% = 12.5\%$.
$$ P(A \cap W) = 12.5\% $$Furthermore, let's calculate the joint probability $P(\overline{W} \cap B)$. ($\overline{W}$ does not mean the direction opposite to $W$, i.e., 180°, but rather the event of obtaining $-1/2$ when measuring in the $W$ direction on the left, or perhaps obtaining $+1/2$ when measuring in the $\overline{W}$ direction (180° different from $W$) on the left. Following the text's notation $P(\overline{W} \cap B)$, we interpret this as the probability that the measurement result in the $W$ direction on the left is $-1/2$, and the measurement result in the $B$ direction on the right is $+1/2$. However, this interpretation might differ from the $P(\overline{W} \cap B)$ used in deriving Bell's inequality. The text might intend $P(\text{Left at }\overline{W}=+1/2 \text{ and Right at } B=+1/2)$. In that case, if $B=60^\circ$ and $W=0^\circ$, then $\overline{W}=180^\circ$, and the angle difference between $\overline{W}$ and $B$ is $180^\circ - 60^\circ = 120^\circ$.) The angle difference is $120^\circ$, so,
$$ P(B|\overline{W}) = \cos^2 \left(\frac{120^\circ}{2} \right) = 25\% $$Assuming $P(\overline{W})=1/2$ (the probability of obtaining $+1/2$ when measuring in the $\overline{W}$ direction on the left), then $P(\overline{W} \cap B) = P(\overline{W}) \times P(B|\overline{W}) = (1/2) \times 25\% = 12.5\%$.
$$ P(\overline{W} \cap B) = 12.5\% $$Now, let's restate Bell's inequality:
The left side of the above inequality is 37.5% and the sum of the right side is 25%. Thus, the predictions of quantum mechanics violate this Bell's inequality.
$$ 37.5\% \gt 12.5\% + 12.5\% $$As such, there exist strange correlations between observation devices $L$ and $R$ that cannot be explained by classical probability theory. These correlations are called EPR correlations and has been confirmed by experiments (e.g., Alain Aspect's experiment in 1982).
Where does the mystery of EPR correlations come from? It is thought to lie in the fact that "the measurement results $A$ and $B$ cannot be broken down into cases based on the unmeasured result $W$ (or $\overline{W}$)." This is similar to the double-slit experiment, where the result cannot be simply divided into cases of the electron passing through the left slit and the electron passing through the right slit, unless which slit the electron passed through is observed.
Here, let's consider why Bell's inequality is violated.
In the previous section, I stated that the mystery of EPR correlations arise from "the inability to classify the measurement results $A, B$ by the unmeasured result $W$." However, surprisingly, it is possible to spatially separate the "state corresponding to the unmeasured result $W$." Before explaining that, I would like to describe how electron spin is measured.
To measure the spin of an electron, a Stern-Gerlach apparatus like the following is used.
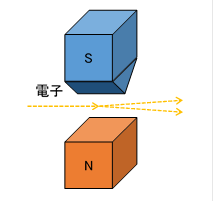
An inhomogeneous magnetic field is created between a pointed S pole and a flat N pole. The magnetic field strength increases closer to the S pole. When an electron beam passes through this inhomogeneous magnetic field, the beam splits into two trajectories depending on the spin orientation. This reveals the direction of the electron's spin (up or down relative to the magnetic field direction). Regardless of the original spin direction, it always splits into one of the two trajectories relative to the direction of the measuring magnetic field.
By combining these Stern-Gerlach apparatuses, the following device can be made.
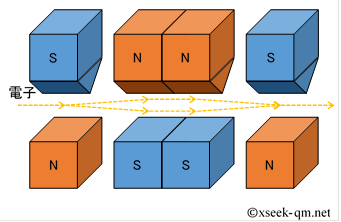
In the device above, the electron beam, once split, recombines again. For later explanation, I will abbreviate the above device with the following diagram.
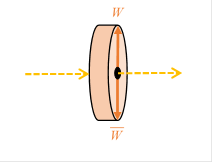
What happens if we place a wall $C$ in the middle of this device?
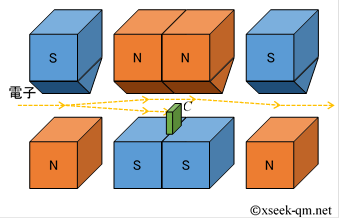
Since the lower trajectory is blocked, it becomes definite which trajectory the electron took (in this case, it took the upper trajectory). For later explanation, I will abbreviate the device including this operation (blocking one path) with the following diagram.
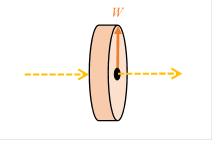
Using these devices, we conduct the following thought experiment.
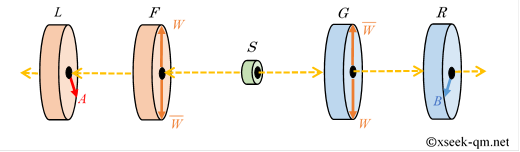
One electron of the EPR pair is first passed through device $F$, which separates and recombines based on direction $W$, and then sent to device $L$, which measures in direction $A$. The other electron is similarly passed through device $G$, which separates and recombines based on direction $W$ (device $G$ might include an operation that swaps paths based on spin direction), and then sent to device $R$, which measures in direction $B$. The electron beam is temporarily separated into trajectories $W$ (spin up) and $\overline{W}$ (spin down) in devices $F$ and $G$ according to spin direction and then recombined, yet EPR correlations still appear between the measurement results of devices $L$ and $R$, potentially violating Bell's inequality.
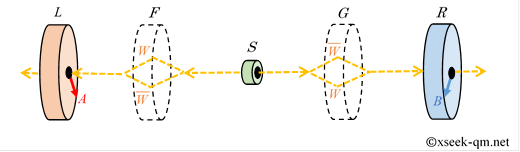
This is a very mysterious result. This is because, while the electron beam is separated into trajectories $W$ and $\overline{W}$, it is possible, in principle, to determine (or force determination of) which path the electron is on (i.e., whether the measurement result for $W$ is +1/2 or -1/2). If we can clearly separate the cases based on the path (= measurement result for $W$), Bell's inequality should hold. Why is Bell's inequality violated?
Indeed, if we perform a measurement that determines the path (e.g., blocking one path) "midway" while the electron beam is separated into trajectories $W$ and $\overline{W}$, Bell's inequality holds. However, if the beam is recombined without determining the path, the possibilities of passing through the two paths "interfere," and as a result, correlations appear that violates Bell's inequality. These correlations indicate that the two distant electrons are still in a single, combined quantum state (entangled state). Therefore, the reasons for the violation of Bell's inequality can be summarized as follows:
In fact, there are several types of inequalities referred to as "Bell's inequality." I will briefly explain each one.
Irish physicist John Bell proposed the first inequality in 1964. It was in a form using the correlation function $C$.
Here $C(A,B)$ represents the strength (expectation value) of the correlations between measurement results in direction $A$ and direction $B$. However, the meaning of this inequality might also be hard to grasp intuitively. Later, Clauser, Horne, Shimony, and Holt (CHSH) proposed the following inequality in 1969, in a form more suitable for experimental verification.
This is also an inequality involving correlation functions. Hungarian physicist Eugene Wigner, around 1970, reformulated Bell's inequality using probabilities, making it easier to understand (a similar form was also shown by d'Espagnat).
Physicist J.J. Sakurai, in his famous textbook "Modern Quantum Mechanics" published in 1994, introduced the probability-based form of the inequality above as Bell's inequality. Here, the function $P(A+;B+)$ represents the joint probability, in the following EPR experiment setup, that the left observation device $L$ observes spin $+1/2$ in direction $A$ ($A+$), and the right observation device $R$ observes spin $+1/2$ in direction $B$ ($B+$).
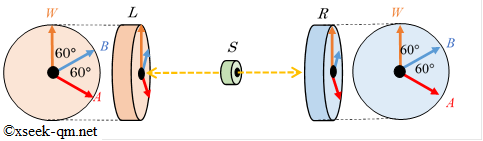
Bell's original inequality (1964) and the CHSH inequality (1969) were about the strength of correlations (expectation value). On the other hand, the Wigner-d'Espagnat inequality (1970) is an inequality of probabilities. Therefore, it became easier to understand the meaning of the inequality than before. However, the meaning of the inequality is still hard to understand. The reason is that the directions $A$, $B$, $W$ of the left observation device $L$ and the directions $A$, $B$, $W$ of the right observation device $R$ are the same direction. It is easier to understand if the direction of the right observation device $R$ is rotated 180 degrees as follows. This is because there is an inverse correlation between the left observation device $L$ and the right observation device $R$.

Based on the EPR experiment above, it is easier to understand the meaning of Bell's inequality if it is expressed using set notation as follows.
$$ P(A \cap B) \leqq P(A \cap W)+P(\overline{W} \cap B) $$In this article, I have explained the inequality above as Bell's inequality. Bell's inequality can be represented by a Venn diagram as follows.
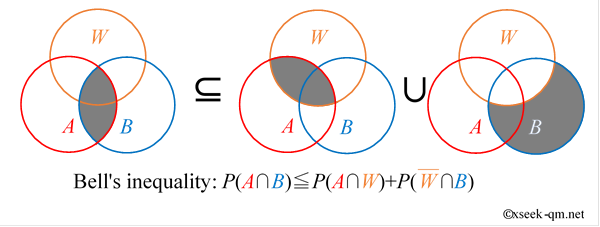
Looking at the Venn diagram above, the meaning of Bell's inequality becomes clear. In fact, French physicist Bernard d'Espagnat also explained Bell's inequality using a Venn diagram in 1979 (Reference link).
Bell's inequality is correct if the weather can be divided into sunny and rainy cases (based on the assumption of local realism). However, in the world of quantum mechanics, unless the weather is observed, it cannot be divided into sunny and rainy cases.
When Alice meets Bob, what answer would they give if asked about the weather that day? Actually, strangely enough, in the quantum world, unless you measure it, the weather condition remains indeterminate.
© 2002-2018 xseek-qm.net
広告


