Many-Worlds Interpretation

[List]

Everett’s Proposal

In 1957 Hugh Everett, a graduate student at Princeton University, published a new interpretation of quantum mechanics. It is now known as Everett’s many‑worlds interpretation.

A commentary on Everett’s original paper can be found here:

Imagine placing a single electron inside a box. Quantum mechanics says the electron spreads throughout the box like a wave, called the wave function. When someone looks inside, the electron appears at one spot and the wave function seems to collapse there.

One might think, “The electron was always a particle and the wave only gives probabilities.” That is incorrect. Alain Aspect’s 1982 experiment ruled out such hidden‑variable explanations. Before measurement, the electron truly is spread out as a wave.

Collapse is deeply puzzling. If the box is divided into two chambers, the electron’s wave occupies both. Open one chamber and you may—or may not—find the electron there.

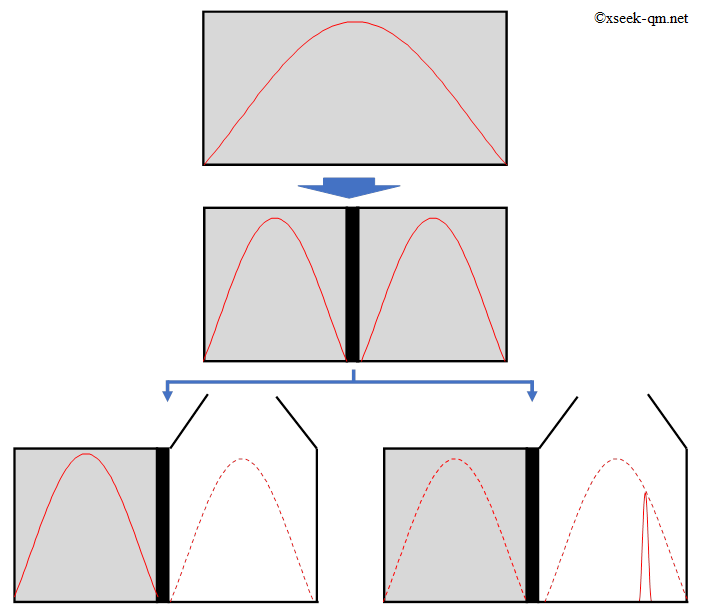
If the electron is found, the wave function contracts to that point; if not, it contracts into the opposite chamber. The fact that the wave changes even when the electron is not seen is stranger still.

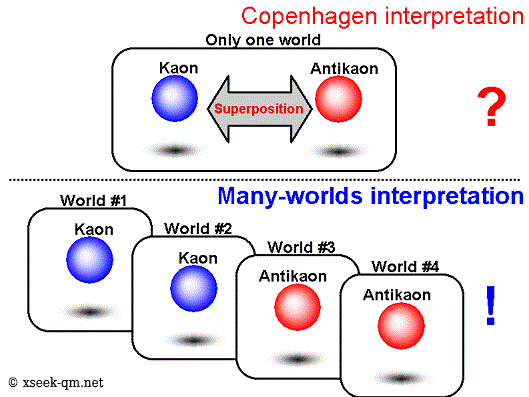
Everett suggested the wave function never collapses. If we describe an electron with a wave function, observers must be described the same way. When someone observes the electron, the observer splits into

1. Observer A, who sees the electron at position x
2. Observer B, who sees the electron at position y
3. Observer C, who sees the electron at position z

Just as the electron is a wave spread through space, the observer becomes a wave spread through many worlds.

My First Encounter with Many‑Worlds

I first learned about many‑worlds in the Japanese popular‑science book “The Fate of the Universe” when I was about ten. It included the following passage (translated):

If, as some science‑fiction writers suggest, the universe splits in two whenever a random event occurs, countless universes would exist—slightly different, greatly different, as many as one can imagine.

(…)

This story is fascinating. Readers might think no scientific theory would accept such an idea, yet one does: the “many‑worlds interpretation” of quantum mechanics, proposed in 1957 by American physicist Hugh Everett III in his Princeton PhD thesis.

(…)

You may expect such a fantastic notion to be easy to disprove, but it is not. Everett’s theory is mathematically identical to the standard formulation of quantum mechanics, so no experiment can presently distinguish between them.

At first I found the idea unbelievable. Later, while studying K‑meson mixing in college—where two distinct particles appear in superposition—I began to feel the many‑worlds view was more natural.

Further Information

The interpretation is discussed in books such as “The World Described by Quantum”, which also covers David Deutsch’s quantum computer.

For a long time textbooks barely mentioned many‑worlds, but “Introduction to Quantum Mechanics” does, albeit critically. In 1994 “The Picture of the World Told by Quantum Mechanics” became one of the first popular books to strongly endorse it.

Quantum mechanics faces the measurement problem—wave‑function collapse and Born’s probability rule. Because many‑worlds rejects collapse, it sidesteps the first half of the problem. However, present formulations still cannot derive Born Rule. I believe the interpretation will need further mathematical extension to be complete.

• The Arrow of Time: Why does time flow only toward the future? (2013/9/28)
• Questions about Many‑Worlds: Frequently asked questions and answers (2014/1/11)
• Many‑Worlds and Born Rule: Attempts to derive the probability rule (2014/9/18)

広告