Electron Wave Functions in Quantum Mechanics

[List]

Electron wave functions of the hydrogen atom

Rotation Axis of Spherical Harmonics in Atomic Orbitals

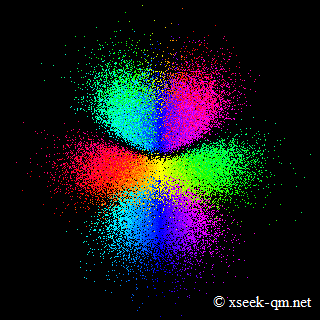
In Bohr's atomic model, electrons are depicted as orbiting the nucleus in fixed orbits. In modern quantum-mechanical models of atomic orbitals like the one below, the electrons do not appear to be orbiting.

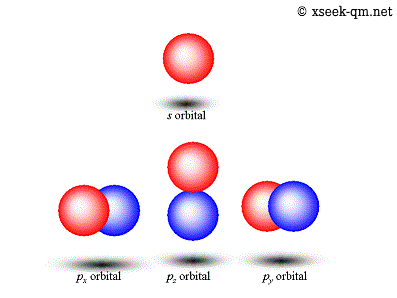
In the second row, the image shows a connection between a red sphere and the orbital’s angular momentum, but the axis of rotation remains unclear.

Meanwhile, on the "Wave Functions Illustrated by Phase" page of the Mathematical Science Art Museum, wave functions are visualized as follows:

1. Amplitude is shown by brightness.
2. Phase is shown by color hue.

With this approach, the motion of electrons around the nucleus can be animated.

I explored animating these visualizations with JavaScript.

Electron Rotation Animation

You can view a GIF animation of the rotating electron wave function in the 4f orbital of the hydrogen atom here:

GIF animation of the rotating electron wave function

The animation is also available on YouTube.

We produced the video using these steps:

1. Use a Monte Carlo method to distribute points according to the probability density.
2. Color each point based on its phase.
3. Animate by varying each point's phase over time.

Altering only the phase makes the wave function appear to rotate.

A JavaScript-based animation of an electron's wave function in a hydrogen atom can be seen here:

JavaScript animation of the electron wave function

Orbital State

The default state is (n, l, m) = (4, 3, 1), where n is the principal quantum number, l is the azimuthal quantum number, and m is the magnetic quantum number.

Click the "State" button to select one of these states: (1, 0, 0), (2, 1, 1), (3, 2, 1), (3, 2, 2), etc. In the (1, 0, 0) state, no rotation occurs; only the global phase changes.

Point Count

The default number of points is 51200. If your computer lacks sufficient performance, reduce the number of points by clicking the "Number" button.

• The Meaning of Bell's Inequality: A Simple Explanation Using Venn Diagrams (2018/9/2)
• Spin in Quantum Mechanics: Demystifying Spin's Mysterious Properties (2014/9/1)
• Many-Worlds Interpretation: Exploring the Concept of Parallel Universes (2013/6/22)

広告