Spin in quantum mechanics is an intrinsic form of angular momentum carried by elementary particles such as electrons.
Water, which we drink every day, is made of hydrogen and oxygen atoms. In a hydrogen atom, an electron orbits a proton. Because atoms are so small, it can be difficult to visualize them. Therefore, we use a "daily unit system" to express atomic dimensions in familiar terms.
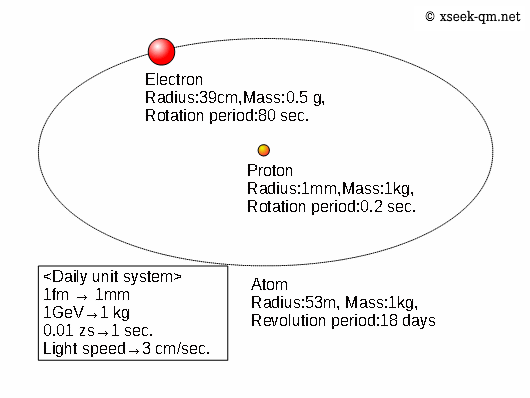
In this figure, the electron’s radius is shown as 390 femtometers (39 centimeters in the daily unit system). In reality, experiments confirm that the electron’s radius is smaller than 1 femtometer (1 millimeter in the daily unit system).
Both protons and electrons have intrinsic spin. In quantum mechanics, this means they possess a fixed angular momentum that does not change.
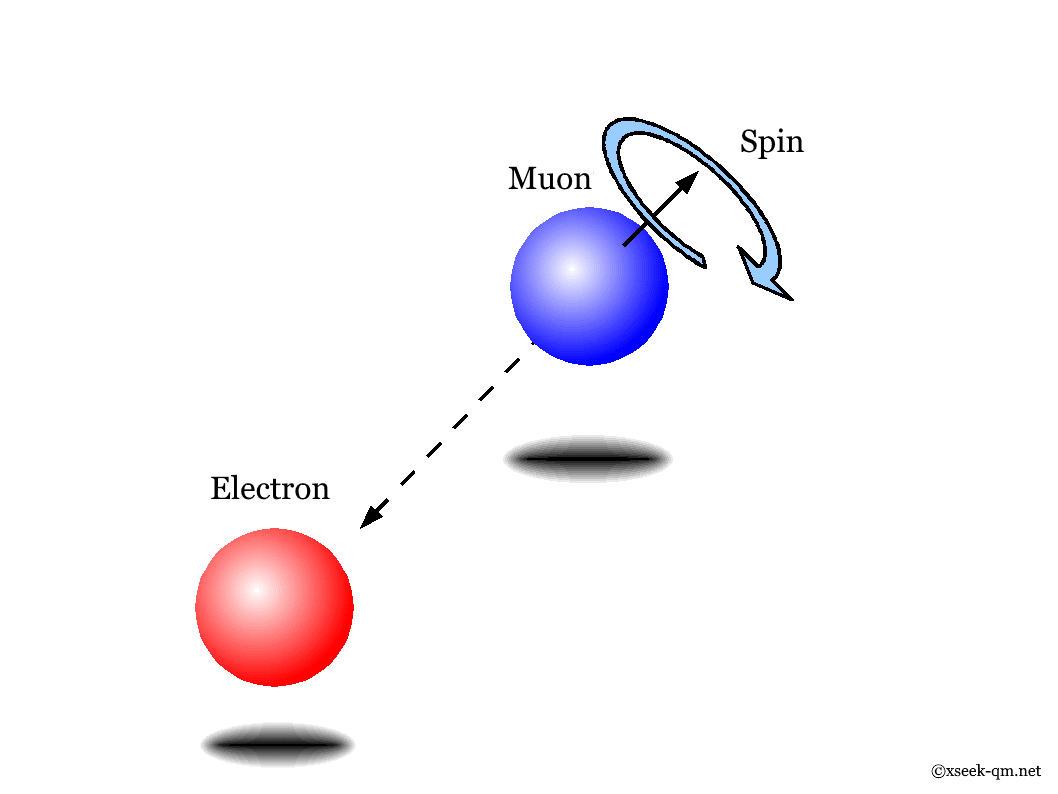
To explain spin further, consider the muon, a particle similar to the electron. Its mass is 106 MeV (106 grams in the daily unit system), and its lifetime is about two microseconds (approximately 700 million years in daily units). The muon decays into two neutrinos and an electron.

Without a magnetic field, the spin axis can orient in any direction. We infer its orientation by observing the decay electron, which is emitted opposite to the muon’s spin.
In a magnetic field, the spin can only take two orientations: parallel or anti-parallel to the field. The spin state is a superposition of these two possibilities, and the decay electron is emitted accordingly. In other words, the magnetic field breaks rotational symmetry.
Many people argue that spin is not a literal rotation, due to two issues.
Experiments show that the electron’s radius is less than 1 femtometer (1 millimeter in daily units). To account for its spin angular momentum by classical rotation, the surface would have to move at 390 times the speed of light. Even using a radius of 390 femtometers (39 centimeters in daily units) yields a rotational speed equal to c.
A 360° rotation changes the sign of the spin-½ wave function, and only after a 720° rotation does it return to its original phase. Hence, the spin wave function is double-valued.
Because of these problems, many do not view spin as literal rotation. To support a rotational interpretation of spin, I wrote the following paper.
I hope this paper helps you understand spin as a rotational phenomenon.
© 2002-2014 xseek-qm.net
広告


