Lorentz contraction effect
This article introduces the Bell spaceship paradox.
E. Dewan and M. Beran first presented the Two Spaceships Paradox in 1959. Later, in 1987, J. S. Bell revisited this thought experiment, and it has since become known as Bell’s Spaceship Paradox.
The paradox is typically illustrated with two spaceships. However, the speed of light is so large that it can be hard to visualize. To simplify, we assume the speed of light is 30 millimeters per second.
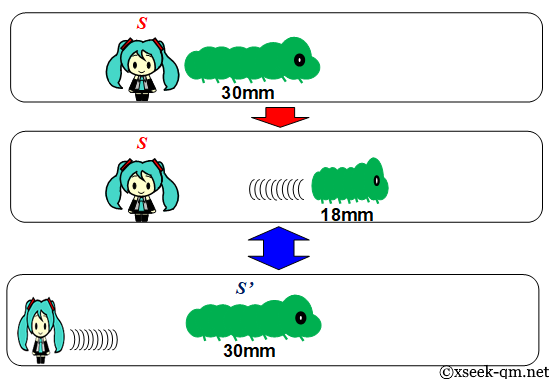
Consider a caterpillar on a desk with a body length of 30 millimeters.

The caterpillar accelerates for 10 seconds and reaches a speed of 24 millimeters per second. What is its contracted length?
The Lorentz contraction formula is given by:
$$ L = L_0 \sqrt{1-\frac{v^2}{c^2}} $$Using L0 = 30 mm, v = 24 mm/s, and c = 30 mm/s, we calculate:
$$ L = 30 \sqrt{1-\frac{24^2}{30^2}} = 18 $$Thus, the contracted length is L = 18 mm. In the caterpillar’s rest frame S′, however, its length remains 30 mm.
Now place two ants on the desk 30 millimeters apart.
Both ants accelerate for 10 seconds, starting and stopping simultaneously in the rest frame S, reaching a speed of 24 mm/s. What is the distance between them in frame S?
One might expect the separation to contract according to Lorentz contraction. However, because both ants begin and end their acceleration simultaneously in S, their separation remains 30 mm in that frame.
Assuming each ant accelerates at a constant rate a = 2.4 mm/s2 for 10 seconds in frame S, we can describe their motion as follows.
Let ant A start at x(0) = 0 mm at t = 0. Its position after time t is:
$$ x(t) = \tfrac{1}{2} a t^2 $$After 10 seconds, x(10) = ½·a·(10 s)2 = 120 mm.
If ant B starts at x(0) = 30 mm, its position y(t) is:
$$ y(t) = 30 + \tfrac{1}{2} a t^2 $$After 10 seconds, y(10) = 30 + ½·a·(10 s)2 = 150 mm.
Thus, the separation remains 150 mm − 120 mm = 30 mm. Both ants then travel at constant velocity v = 24 mm/s, so they maintain a 30 mm separation in frame S.
Now imagine a thread connecting the two ants. What happens to the thread when the ants begin to accelerate?
When the ants accelerate, the thread breaks. This seems counterintuitive in frame S, where their separation remains constant. Why does the thread break?
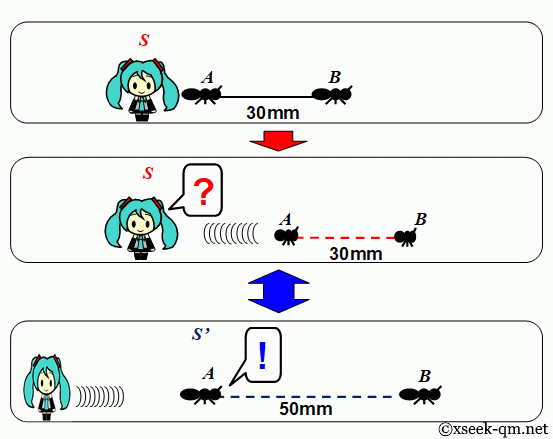
In ant A’s rest frame S′, the relativity of simultaneity causes ant B to finish accelerating before ant A. Consequently, B attains a higher velocity temporarily, increasing their separation. In S′, the distance grows to 50 mm, causing the thread to break.
This paradox arises because, even though the ants’ separation in S is unchanged, the thread’s internal forces cannot adjust instantaneously. The resulting stress causes the thread to snap.
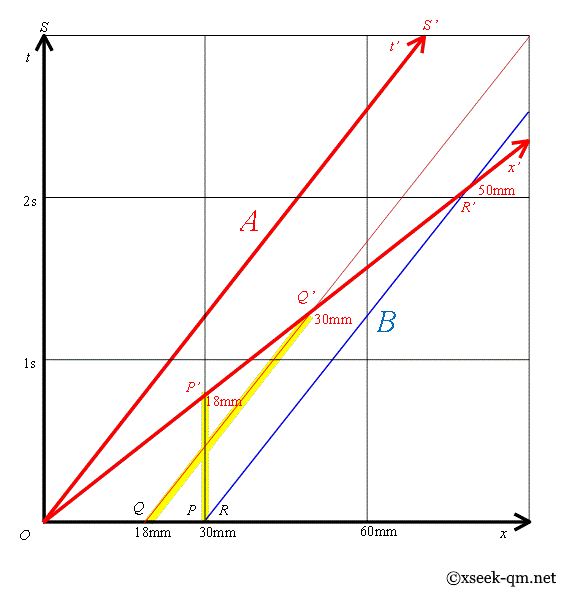
We can understand Lorentz contraction via Minkowski spacetime.
The Lorentz transformation equations are:
$$ x' = \gamma (x - \beta ct) $$ $$ ct' = \gamma (ct - \beta x) $$where γ and β are defined as:
$$ \gamma = \frac{1}{\sqrt{1-\beta^2}} $$ $$ \beta = \frac{v}{c} $$Using v = 24 mm/s and c = 30 mm/s, we obtain:
$$ x' = \frac{5}{3} \bigl(x - \tfrac{4}{5} ct\bigr) $$ $$ ct' = \frac{5}{3} \bigl(ct - \tfrac{4}{5} x\bigr) $$In spacetime, the world line of ant A is curve A, and that of ant B is curve B. In frame S, their separation corresponds to segment OR, while in frame S′ it corresponds to segment OR′.
Similarly, the caterpillar’s rest length is represented by segment OQ in S, and its contracted length by segment OQ′ in S′.
Here, we focus on the cross-shaped structure formed by segments PP′ and QQ′. This, I propose, captures the essential geometric feature of the Lorentz transformation.
© 2002, 2015 xseek-qm.net
広告


