
In 1907, while working at the patent office, Einstein conceived what he called “the greatest thought of my life”: the equivalence principle. It says that the two situations below are locally identical:
Imagine an elevator cabin on the ground with a person inside. Tell the person, “This cabin is floating in space.”
The person feels pressed against the floor, and therefore concludes that the cabin must be accelerating upward.
Thus, by the equivalence principle, we can picture all of space around us as falling toward Earth with an acceleration of 9.8 m/s2.
Let us examine gravity through the lens of the equivalence principle. Newton’s law gives gravitational acceleration as
where g, G, M, and R are defined below.
| Gravitational acceleration g | 9.8 m/s2 |
| Gravitational constant G | 6.7×10−11 m3/s2 kg |
| Earth’s mass M | 6.0×1024 kg |
| Earth’s radius R | 6 400 km |
Multiplying both sides by 4πR2 gives
Interpreted through the equivalence principle, Earth can be viewed as a spherical shell of radius R that accelerates and “draws in” a volume of space equal to 4πR2×9.8 m3. Likewise, the right‑hand side represents Earth drawing in 4π×6.7×10−11×M m3. Because our universe has three spatial dimensions, this effect diminishes with the square of the distance.
Einstein spent eight years turning the equivalence principle into mathematics and finally realized that gravity could be described as the curvature of spacetime. That insight culminated in his general theory of relativity in 1915.
The next figure illustrates spacetime curvature.
The blue line shows an object at rest in the absence of gravity. The red line shows an object falling to the right in a gravitational field.
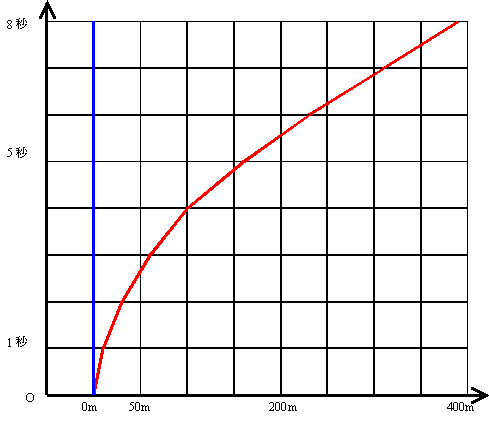
If a moving object is viewed as stationary in free space, its world‑line itself represents curved spacetime.
To visualize general relativity, educators often use a curved rubber sheet to stand in for space, but in truth it is spacetime—not just space—that is curved.
To see how matter and curvature relate, consider Einstein’s field equation:
Here Gμν is a geometric quantity and Tμν a matter quantity, showing that matter tells spacetime how to curve. Einstein wrote in his 1936 essay “Physics and Reality”:
[General Relativity] is sufficient — as far as we know — for the representation of experiences of celestial mechanics. But it is similar to a building, one wing of which is made of fine marble (left side of the equation), but the other wing of which is built of low-grade wood (right side of equation). The phenomenological representation of matter is, in fact, only a crude substitute for a representation which would do justice to all known properties of matter.
Einstein’s metaphor suggests that the right‑hand side should also be geometric— in other words, matter itself may need a geometric description.
What ultimately causes gravity? Einstein’s equation links matter to curvature but does not explain why matter bends spacetime. How does matter accomplish this?
Mathematician William K. Clifford wrote in 1870 to the Cambridge Philosophical Society (quoted in Introduction to Superstring Theory):
- That small portions of space are in fact of a nature analogous to little hills on a surface which is on the average flat; namely, that the ordinary laws of geometry are not valid in them.
- That this property of being curved or distorted is continually being passed on from one portion of space to another after the manner of a wave.
- That this variation of the curvature of space is what really happens in that phenomenon which we call the motion of matter, whether ponderable or ethereal.
Thus matter itself may be nothing but curved space. If so, both sides of Einstein’s equation would be geometric, and the origin of gravity might be revealed. For now, its true cause remains unknown. Will you take up the challenge?
© 2013-2014 xseek-qm.net
広告


