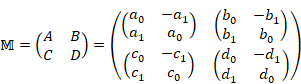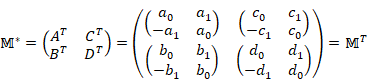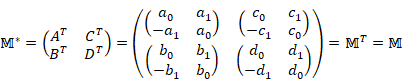なぜ虚数単位iの2乗は-1になるのか?
2019/3/2
公開日 2014/6/29
Koji Sugiyama
虚数単位iの2乗が-1になる理由を説明します。
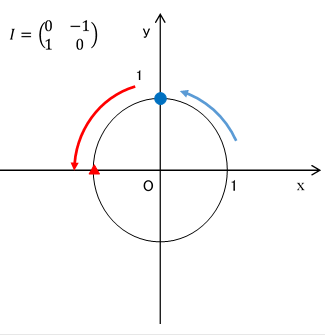
図 2-9: 回転単位行列は反時計周りに90度回転する。
オイラーは1777年に虚数単位の記号iを導入し、次の式を示しました。
i2 = -1
これはとても不思議な式です。なぜ数の2乗が-1になるのでしょうか?
オイラー、ガウス、ハミルトンが、この式の秘密を解き明かしてきました。この式の秘密を知りたいと思っている方に、ぜひ、この記事を読んでほしいと思います。
要旨は次のとおりです。
(1) 虚数単位を行列の略記と解釈する。
(2) 虚数単位を画像の90度回転と解釈する。
(3) -1を画像の180度回転と解釈する。
(4) 画像を2回、90度回転すると180度回転になる。
虚数を行列の略記と解釈する理由を理解するため、この記事では、行列の幾何学的な解釈について説明したいと思います。
目次
本論では、次の等式が成立する理由を説明します。
(虚数単位の等式)
|
|
(1.1) |
行列を理解するため、画像の変換を考えてみましょう。
次のように、点(x, y )を点(x’, y’ )へ移動させます。
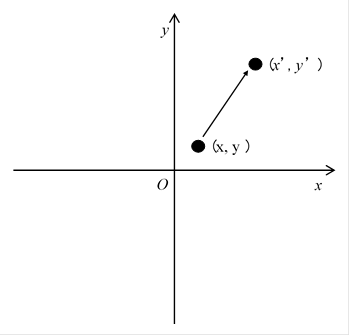
図 2-1: 行列は点 (x, y) を点 (x’, y’ ) に移動する。
この変換を次の式で表現します。
|
|
(2.1) |
この変換は一次変換と呼ばれています。
一次変換の式は複雑です。そこでもっと簡単に書くため、次の略記で表現します。
|
|
(2.2) |
上記の「一次変換の略記」を行列と呼びます。
この行列は点 (1, 0) と点 (0, 1) を次のように移動します。
|
|
(2.3) |
|
|
(2.4) |
点 (1, 0) の移動先は行列の一列目a, cで作った座標(a, c)になります。
点 (0, 1) の移動先は行列の二列目b, dで作った座標(b, d)になります。
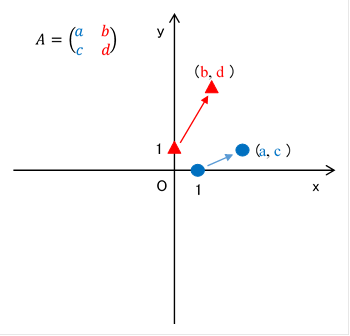
図 2-2: 点(1,0)の移動先は行列の成分(a, c)となり、点(0,1)の移動先は行列の成分(b, d)となる。
一次変換から行列の演算規則を導いてみましょう。
一次変換は次のとおりです。
|
|
(2.5) |
こうして得られた点(x’, y’ ) をもう一度、一次変換してみましょう。
|
|
(2.6) |
次に、式(2.5)を式(2.6)に代入し計算してみましょう。すると次の式が得られます。
|
|
(2.7) |
式(2.5)、(2.6)、(2.7)は複雑です。そこでもっと簡単に書くため、次のように略記することにしましょう。
一方、式(2.8)の左辺を一つの値と解釈し、その値を式(2.9)に代入してみましょう。すると、次の式が得られます。
|
|
(2.11) |
式(2.10)と式(2.11)を比較してみましょう。すると、次の式が得られます。
|
|
(2.12) |
上記の等式を、行列の演算規則と定義します。
この行列の演算規則はイギリスの数学者アーサー・ケイリー [1] が1858年に定義しました。
行列は画面全体を変換するので、図示するのが難しいです。そこで、行列が変換した単位円を観察することにしましょう。
たとえば、次の行列を考えます。
|
|
(2.13) |
この行列で、次の単位円はどのように変換されるのでしょうか?
|
|
(2.14) |
それは次の楕円となります。

図 2-3: 行列の円周変換図
青い丸●は点 (1, 0) の移動先を意味します。赤い三角▲は点 (0, 1) の移動先を意味します。点線は楕円の主軸と副軸です。本記事では、このような行列の表現方法を「円周変換図」と呼ぶことにしましょう。
上記の図を見ると、楕円の主軸が固有ベクトルのように見えます。しかし、常にそうではありません。一般的に、主軸は次の図のように固有ベクトルと異なります。
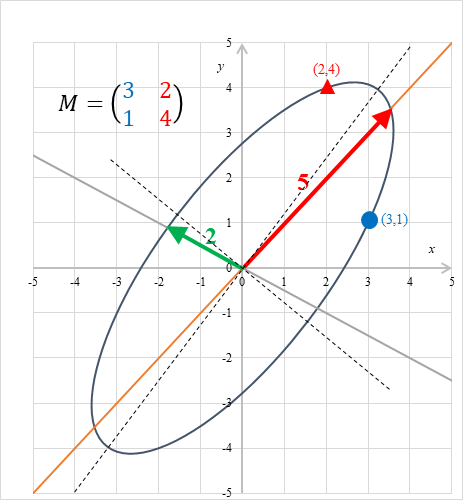
図 2-4: 楕円の主軸は行列の固有ベクトルと異なる。
後述の特異値分解によれば、一般的な行列を次の4種類の連続操作で表現できます。
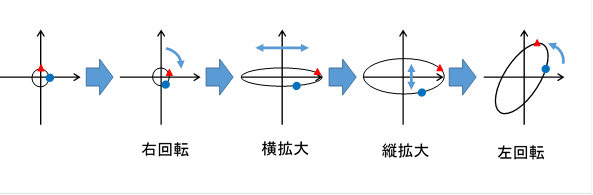
図 2-5: 行列は右回転、横拡大、縦拡大、左回転に分解できる。
行列は回転と拡大で表現できます。そこで、以下の節では回転と拡大について説明します。
次の行列を考えてみましょう。
|
|
(2.15) |
これは回転行列と呼ばれています。回転行列は次の行列で表現できます。
|
|
(2.16) |
円周変換図では次のとおりです。
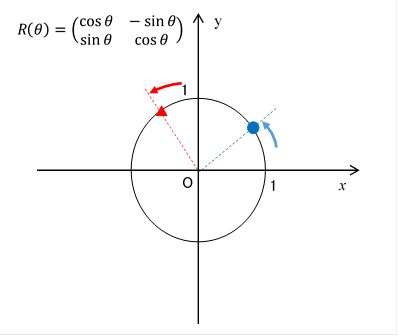
図 2-6: 回転行列
右回転は次のように表現できます。
|
|
(2.17) |
x軸方向を2倍に拡大する行列は次のように表現できます。
|
|
(2.18) |
本記事では、この行列を横拡大行列と呼ぶことにします。
円周変換図では次のとおりです。

図 2-7: 横拡大行列は横方向に拡大変換する。
縦に拡大する行列も横拡大行列と同じ方法で作ることができます。
本記事では、縦に拡大する行列を縦拡大行列と呼ぶことにします。
次の行列を考えてみましょう。
|
|
(2.19) |
この行列は単位行列の実数倍で表現できます。
本記事では、この行列を拡大行列と呼ぶことにします。
|
|
(2.20) |
|
|
(2.21) |
本記事は、単位行列を実数単位行列または拡大単位行列と呼ぶことにします。
縦と横の拡大率が同じ変換は次の行列で表現できます。
|
|
(2.22) |
円周変換図では次のとおりです。
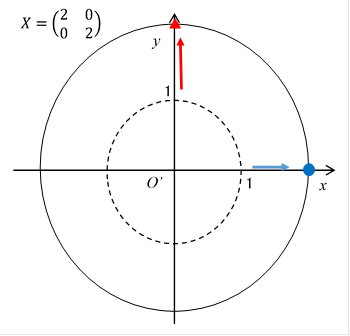
図 2-8: 拡大行列は均等に拡大する。
次の行列を考えてみましょう。
|
|
(2.23) |
本記事では、これを虚数単位行列、または回転単位行列と呼ぶことにします。
90度の回転は、次の行列で表現できます。
|
|
(2.24) |
円周変換図では次のとおりです。

図 2-9: 回転単位行列は反時計周りに90度回転する。
任意の行列は次のように分解できます。
(1) 右回転
(2) 横拡大
(3) 縦拡大
(4) 左回転
この分解は特異値分解と呼ばれています。
横拡大率が縦拡大率と等しい場合、拡大と回転は順序を交換できます。その場合、任意の行列は次のように分解できます。
(1) 回転
(2) 拡大
この可換性が、複素数の可換性の起源となります。
複素数を行列の略記と解釈する理由を理解するために、次の行列を考えてみましょう。
|
|
(3.1) |
本記事では、この行列を虚数単位行列、または回転単位行列と呼ぶことにします。
この行列は次の式を満たします。
|
|
(3.2) |
|
|
(3.3) |
本記事では、行列Eを拡大単位行列と呼ぶことにします。
ここで次の行列を定義します。
|
|
(3.4) |
|
|
(3.5) |
本記事では、この行列Zを拡大回転行列と呼ぶことにします。この行列を次のように略記します。
|
|
(3.6) |
|
|
(3.7) |
上記のように「拡大回転行列の略記」を複素数と呼びます。
元の行列は「複素数の行列表現」と呼ばれています。
レオンハルト・オイラー [2]は1748年に次の公式を発見しました。
(オイラーの公式)
|
|
(3.8) |
複素数の行列表現は次のとおりです。
|
|
(3.9) |
右辺は成分で次のように表現できます。
|
|
(3.10) |
右辺は次の回転行列に一致しています。
|
|
(3.11) |
本記事では、次のことを説明しました。
- 複素数を拡大回転行列の略記と解釈できる。
したがって、虚数単位は虚数単位を行列の略記と解釈できます。虚数単位を画像の90度回転と解釈できます。また-1を画像の180度回転と解釈できます。
2回の90度回転は180度回転と等しいです。そのため、虚数単位の2乗が-1になる理由を幾何学的に理解できます。
転置行列とは、行列の行と列の成分を入れ替えた行列です。
|
|
(5.1) |
|
|
(5.2) |
転置行列を次のように表現することもあります。
|
|
(5.3) |
ですが、本記事は次の表記を採用します。
|
|
(5.4) |
転置行列と元の行列の違いは何でしょうか?これを考えるために次の行列を導入してみましょう。
|
|
(5.5) |
転置行列を次のように解釈してみましょう。
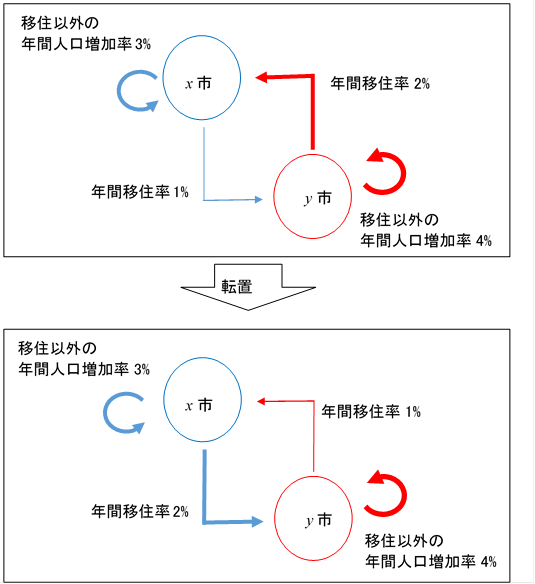
図 5-1: 転置行列
上記の図において、x市からy市への移住率と、y市からx市への移住率は等しくありません。これらの移住率を入れ替える操作が転置なのです。
これらの移住率が等しい場合、行列は後述の対称行列となります。
転置行列と元の行列が等しい場合、その行列は対称行列と呼ばれます。
|
|
(5.6) |
次のような行列は対称行列です。
|
|
(5.7) |
対称行列では、円周変換図の主軸は固有ベクトルに等しくなります。

図 5-2: 対称行列では、円周変換図の主軸は固有ベクトルに等しい。
オーギュスタン=ルイ・コーシー [3]は1829年に対称行列の固有値がすべて実数であることを証明しました。
行列式とは、行列による面積の拡張率と解釈できます。
行列式は、次のように表現できます。
|
|
(5.8) |
行列式はオーギュスタン=ルイ・コーシー [4]が1815年に定義しました。
2次元行列の行列式は面積拡張率と解釈できます。
3次元行列の行列式は体積拡張率と解釈できます。
固有ベクトルとは、ある行列の変換で、その方向が変わらないベクトルです。固有値とは、その固有ベクトルの拡大率です。
対称行列の場合、円周変換図の主軸が固有ベクトルです。その方向の拡大率が固有値です。
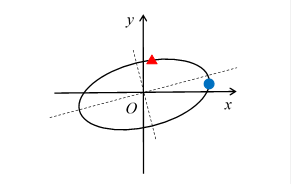
図 5-3: 対称行列では、円周変換図の主軸は固有ベクトルに等しい。
固有方程式とは、固有値を求める方程式のことです。固有方程式は次のとおりです。
|
|
(5.9) |
固有方程式を行列の成分で書けば次のとおりです。
|
|
(5.10) |
なぜ、固有方程式で、固有値を求めることができるのでしょうか?この理由を理解するため、変数λを変化させて、行列 A−λE の変化を観察します。
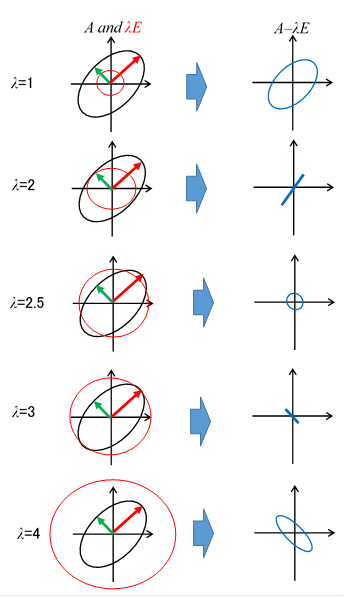
図 5-4: 固有方程式で固有値を導出できる仕組み
黒い楕円は、行列Aで変換した円です。赤い円は、行列 λ E で変換した円です。青い楕円は行列 A−λE で変換した円です。赤の矢印と緑の矢印は、固有値の長さを持つ固有ベクトルです。赤い円の半径が、これらの矢印の一つの長さと一致するとき、行列式はゼロになります。
青い円の面積がゼロならば、面積の拡張率は0です。そのため、変数λを変化させ、面積拡大率がゼロになる変数λの値を探していると解釈できます。
対称行列の場合、一つの固有ベクトルは楕円の主軸と等しいです。そのため、赤い円が黒い楕円に接するとき、赤い円の半径が、これらの矢印の一つの長さと一致します。
特異値分解とは、次の分解です。
・任意の行列Mは回転行列 R(-θ) と対角行列 D と回転行列 ![]() の積に分解できる。
の積に分解できる。
|
|
(5.11) |
特異値分解で、一般的な行列を次の4種類の連続操作で表現できます。

図 5-5: 行列は右回転、横拡大、縦拡大、左回転に分解できる。
横拡大率と縦拡大率は特異値と呼ばれています。それは一般に固有値と等しくありません。対称行列では、横拡大率と縦拡大率が固有値となります。
特異値分解は、ユージニオ・ベルトラミ [5] とカミーユ・ジョルダン [6] が1873年と1874年にそれぞれ独立に発見しました。
実数とは、「拡大単位行列の実数倍」の略記です。
拡大単位行列は次のとおりです。
|
|
(5.12) |
この行列を表現するため、次のような略記を使用します。
|
|
(5.13) |
実数の行列を次のように表現します。
|
|
(5.14) |
実数の行列を表現するため、次のような略記を使用します。
|
|
(5.15) |
虚数とは、「回転単位行列の実数倍」の略記です。
回転単位行列は次のとおりです。
|
|
(5.16) |
この行列を次のように記号iで略記します。
|
|
(5.17) |
虚数の行列を次のように表現します。
|
|
(5.18) |
虚数の行列を次のように略記します。
|
|
(5.19) |
複素数とは、拡大回転行列の略記です。
拡大回転行列は次のとおりです。
|
|
(5.20) |
複素数の行列を次のように表現します。
|
|
(5.21) |
|
|
(5.22) |
|
|
(5.23) |
複素数の行列を次のように略記します。
|
|
(5.24) |
共役複素数は、複素数の虚数成分の符号を変更して構成します。
今、複素数を次のように表現します。
|
|
(5.25) |
数学では共役複素数を上記のように表現します。
|
|
(5.26) |
一方、物理では共役複素数を次のように表現します。
|
|
(5.27) |
本記事は、数学の次の記法を採用します。
|
|
(5.28) |
複素数の行列表現の場合、複素共役は次のような転置行列で表現されます。
|
|
(5.29) |
|
|
(5.30) |
複素共役は転置行列と解釈できます。したがって、任意の行列を転置する場合、任意の複素数を共役複素数に変更する必要があります。
随伴行列は各要素の複素共役を取った転置行列です。
その行列は、次のような名前でも呼ばれています。
- エルミート共役
- エルミート転置
- エルミート随伴
- 共役転置
今、ある行列を次のように表現します。
|
|
(5.31) |
数学では、随伴行列は次のように記述されます。
|
|
(5.32) |
物理学では次のように記述されます。
|
|
(5.33) |
本記事は数学の次の表記法を採用します。
|
|
(5.34) |
複素数の行列表現 A, B, C, D を要素に持つ行列
![]() を次のように定義します。
を次のように定義します。
|
|
(5.35) |
複素数の行列表現を要素に持つ行列では随伴行列は転置行列です。
|
|
(5.36) |
随伴行列が元の行列と等しい場合、その行列は自己随伴行列と呼ばれます。
|
|
(5.37) |
この行列は、エルミート行列とも呼ばれています。
シャルル・エルミート [7]は、1855年にエルミート行列のすべての固有値が実数であることを示しました。
複素数の行列表現 A, B, C, D を要素に持つ行列
![]() を次のように定義します。
を次のように定義します。
|
|
(5.38) |
複素数の行列表現を要素に持つ行列ではエルミート行列は対称行列です。
|
|
(5.39) |
ハミルトンは、1843年に四元数を導入しました。四元数は次の行列の略記と解釈できます。
|
|
(6.1) |
四元数の行列を次のように表現します。
|
|
(6.2) |
|
|
(6.3) |
|
|
(6.4) |
|
|
(6.5) |
|
|
(6.6) |
四元数の行列を次のように略記します。
|
|
(6.7) |
共役四元数とは、虚数成分の符号を変更した四元数です。
|
|
(6.8) |
|
|
(6.9) |
物理的には空間反転を意味します。
四元数の行列表現では、共役四元数は随伴行列です。
|
|
(6.10) |
|
|
(6.11) |
3次元ベクトルuと3次元ベクトルvの内積は次のように定義されています。
|
|
(6.12) |
|
|
(6.13) |
|
|
(6.14) |
しかし、なぜ内積は上記のような定義なのでしょうか?
この理由を理解するために、四元数qと四元数pの割り算を考えてみましょう。
|
|
(6.15) |
四元数Rで、次の回転を定義します。
|
|
(6.16) |
四元数 p を p’へ回転します。
|
|
(6.17) |
四元数 q を q’へ回転します。
|
|
(6.18) |
回転 R に対し四元数 s は不変です。
|
|
(6.19) |
四元数 s を次のように変形します。
|
|
(6.20) |
一方、四元数 s は次のように表現できます。
|
|
(6.21) |
回転 R は四元数 p, q の絶対値を変えません。したがって、四元数 r は回転変換 R に対し不変です。
式(6.20)と式(6.21)で次の等式を作ります。
|
|
(6.22) |
上記の式を次のように変形します。
|
|
(6.23) |
回転Rに対し四元数 p, q の絶対値は不変です。
回転Rに対し四元数 rも不変です。
したがって、回転Rに対し左辺は不変です。
本記事では、左辺を回転不変積と呼ぶことにします。回転不変積が回転で不変なことは、次のように確認できます。
|
|
(6.24) |
|
|
(6.25) |
|
|
(6.26) |
回転不変積の実数成分と虚数成分は回転不変量です。
3次元ベクトルの内積は、純虚数の四元数の回転不変積の実数成分と解釈できます。
|
|
(6.27) |
|
|
(6.28) |
|
|
(6.29) |
|
|
(6.30) |
3次元ベクトル u と3次元ベクトル v の外積は次のように定義されています。
|
|
(6.31) |
|
|
(6.32) |
|
|
(6.33) |
しかし、なぜ外積は上記のような定義なのでしょうか?
実は、3次元ベクトルの外積は、純虚数の四元数の回転不変積の虚数成分の符号反転と解釈できます。
|
|
(6.34) |
|
|
(6.35) |
|
|
(6.36) |
|
|
(6.37) |
ノルウェーの測量技師カスパー・ヴェッセルが1797年に複素平面を発表しました。複素平面とは複素数を幾何学的に表現するための平面です。
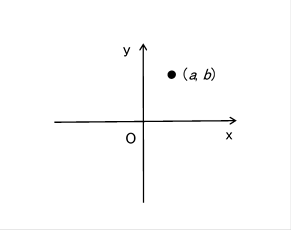
図 6-1: 複素数a+biは点(a,b)として複素平面に存在する。
フランスの数学者ジャン=ロベール・アルガンも1806年に複素平面を発表しました。1831年には、ドイツの数学者カール・フリードリヒ・ガウスが複素平面を使用しました。
ハミルトンは1835年に複素数a + biを(a, b)と表現し、その和と積の演算を次のように定義しました。
|
|
(6.38) |
|
|
(6.39) |
2次元ベクトルuと2次元ベクトルvの内積は次のように定義されています。
|
|
(6.40) |
|
|
(6.41) |
|
|
(6.42) |
しかし、なぜ内積は上記のような定義なのでしょうか?
この理由を理解するために、複素数qと複素数pの割り算を考えてみましょう。
|
|
(6.43) |
複素数Rで、次の回転を定義します。
|
|
(6.44) |
複素数 p を p’へ回転します。
|
|
(6.45) |
複素数 q を q’へ回転します。
|
|
(6.46) |
回転 R に対し複素数 s は不変です。
|
|
(6.47) |
複素数 s を次のように変形します。
|
|
(6.48) |
一方、複素数 s は次のように表現できます。
|
|
(6.49) |
回転 R は複素数 p, q の絶対値を変えません。したがって、複素数 r は回転変換 R に対し不変です。
式(6.20)と式(6.21)で次の等式を作ります。
|
|
(6.50) |
上記の式を次のように変形します。
|
|
(6.51) |
回転Rに対し複素数 p, q の絶対値は不変です。
回転Rに対し複素数 rも不変です。
したがって、回転Rに対し左辺は不変です。
本記事では、左辺を回転不変積と呼ぶことにします。回転不変積が回転で不変なことは、次のように確認できます。
|
|
(6.52) |
|
|
(6.53) |
|
|
(6.54) |
回転不変積の実数成分と虚数成分は回転不変量です。
2次元ベクトルの内積は、複素数の回転不変積の実数成分と解釈できます。
|
|
(6.55) |
|
|
(6.56) |
|
|
(6.57) |
|
|
(6.58) |
2次元ベクトル u と2次元ベクトル v の外積は次のように定義されています。
|
|
(6.59) |
|
|
(6.60) |
|
|
(6.61) |
しかし、なぜ外積は上記のような定義なのでしょうか?
実は、2次元ベクトルの外積は、複素数の回転不変積の虚数成分と解釈できます。
|
|
(6.62) |
|
|
(6.63) |
|
|
(6.64) |
|
|
(6.65) |
本節では、数学用語の由来を分類し、研究と学習の観点で分析します。
数学用語の由来は次のように分類できます。
(1) 人名:対象の発見者の人名に由来するもの
(2) 音声:対象の発見国での名前の音声に由来するもの
(3) 形状:対象の形状に由来するもの
(4) 性質:対象の性質に由来するもの
(5) 役割:対象の役割に由来するもの
それぞれの由来の例を次に挙げます。
(1) 人名:対象の発見者の人名に由来するもの
・エルミート行列
・オイラーの公式
(2) 音声:対象の発見国での名前の音声に由来するもの
・スカラー
・ベクトル
(3) 形状:対象の形状に由来するもの
・行列
・行列式
・複素数
・四元数
(4) 性質:対象の性質に由来するもの
・実数
・虚数
・固有値
(5) 役割:対象の役割に由来するもの
・拡大
・回転
これらの由来を分析する観点は次のとおりです。
- 研究
- 学習
上記の観点に基づいて、それぞれの由来を分析し、最後に分析の結果を説明します。
研究の観点では「人名」は優れています。なぜなら、その対象を、一意に特定できるためです。しかし学習の観点では「人名」は難しいと思います。たとえば「エルミート行列」という名前からは、それから何かを推測することは非常に困難です。
研究の観点では「音声」は優れています。なぜなら、その対象を、一意に特定できるためです。しかし学習の観点では「音声」は難しいと思います。たとえば、ベクトルの意味を知らなかったならば、「ベクトル」という名前から、それが何を意味するかを推測することは非常に困難です。
研究の観点では「形状」「性質」は優れています。なぜなら、それらは抽象度が高く応用範囲が広いためです。しかし、学習の観点では「形状」「性質」は、難しくはありませんが、決して易しいとは言えません。たとえば「行列式」という名前からは「その行列に固有の式であること」を推定できますが、その役割は推定できません。
研究の観点では「役割」は劣っています。なぜなら、それは抽象度が低く応用範囲が狭いためです。しかし、学習の観点では「役割」は易しいと思います。たとえば「回転行列」という名前ならば、「回転するための行列であること」を推定できます。
結論として、学習のみを目的とする初級者は「役割」で呼び、学習と研究の両方を目的とする中級者は「形状」「性質」で呼び、研究のみを目的とする上級者は「人名」「音声」で呼ぶのが望ましいと考えます。
6.3.1. 行列式の由来
ドイツの数学者ガウスは1801年に行列式を「決定するもの (Determinante)」と呼びました。日本では高木貞治が1930年に著書「代数学講義」で「行列式」という用語を用いています。「行列式」という名前には「その行列に固有の式」という意味が込められていると推測します。
学習の観点では拡張式と呼ぶのが望ましいと思います。
6.3.2. 行列の由来
イギリスの数学者シルベスター [8]は、1851年に行列を「生み出すもの (Matrix)」と呼びました。日本では高木貞治が1930年に著書「代数学講義」で「行列」という用語を用いています。「行列」という名前には「行と列に並べられた複数の数字から構成された物」という意味が込められていると推測します。
学習の観点では変換と呼ぶのが望ましいと思います。
6.3.3. 複素数の由来
ドイツの数学者ガウスは1831年に複素数を「複合した数 (Komplexe Zahl)」と呼びました。日本では藤澤利喜太郎が1895年に著書「算術条目及教授法(さんじゅつじょうもく および きょうじゅほう)」で「複素数」という用語を用いています。「複素数」という名前には「二種類の要素が複合した数」という意味が込められていると推測します。
学習の観点では複素変換と呼ぶのが望ましいと思います。
6.3.1. 実数の由来
フランスの数学者デカルト [9]は1637年に、複素数の実部を「現実の数 (Nombre reel)」と呼びました。日本では木村駿吉が1897年に著書「四元法講義」で「実数」という用語を用いています。「実数」という名前には、「現実に存在する数」という意味が込められていると推測します。
学習の観点では、複素数の実部は拡大部と呼ぶのが望ましいと思います。
6.3.2. 虚数の由来
フランスの数学者デカルト [9]は1637年に、複素数の虚部を「想像上の数 (Nombre imaginaire)」と呼びました。日本では木村駿吉が1897年に著書「四元法講義」で「虚数」という用語を用いています。「虚数」という名前には、「現実には存在しない数」という意味が込められていると推測します。
学習の観点では、複素数の虚部は回転部と呼ぶのが望ましいと思います。
6.3.3. 四元数の由来
イギリスの数学者ハミルトンは1843年に四元数を「四つ一組のもの (Quaternion)」と呼びました。日本では木村駿吉が1897年に著書「四元法講義」で「四元数」という用語を用いています。「四元数」という名前には「四つの元を組み合わせた数」という意味が込められていると推測します。
学習の観点では四元変換と呼ぶのが望ましいと思います。
6.3.4. スカラーの由来
イギリスの数学者ハミルトンは1846年に四元数の実部を「大きさを増減させるもの (Scalar)」と呼びました。日本では木村駿吉が1897年に著書「四元法講義」で「スケーラー」という用語を用いています。「スカラー」という名前には「拡大、または縮小する変換」という意味が込められていると推測します。
学習の観点では拡大量と呼ぶのが望ましいと思います。
6.3.5. ベクトルの由来
イギリスの数学者ハミルトンは1846年に四元数の虚部を「運ぶもの (Vector)」と呼びました。日本では木村駿吉が1897年に著書「四元法講義」で「ヴエクトル」という用語を用いています。「ベクトル」という名前には「対象を運ぶ変換」という意味が込められていると推測します。
学習の観点では移動量と呼ぶのが望ましいと思います。
ドイツの数学者ヒルベルトは1904年に固有ベクトルを「固有のベクトル (Eigenvektor)」と呼びました。また固有値を「固有の値 (Eigenwerte)」と呼びました。これが日本語の固有ベクトル、固有値の語源になりました。固有ベクトル、固有値という名前には「その行列に固有のベクトル、値」という意味が込められていると推測します。
学習の観点では固有ベクトルを「拡大軸」、固有値を「拡大値」と呼ぶのが望ましいと思います。
エルミート行列は、フランスの数学者エルミートの名前に由来します。
学習の観点では複素対称変換と呼ぶのが望ましいと思います。
オイラーの公式は、数学者オイラーの名前に由来します。
学習の観点ではオイラーの回転公式と呼ぶのが望ましいと思います。
本記事は、数学用語の呼び方として次の内容を提案します。
|
# |
数学用語 |
提案する呼び方 |
|
1 |
行列式 |
拡張式 |
|
2 |
行列 |
変換 |
|
3 |
複素数 |
複素変換 |
|
4 |
実部 |
拡大部 |
|
5 |
虚部 |
回転部 |
|
6 |
虚数単位 |
回転単位 |
|
7 |
四元数 |
四元変換 |
|
8 |
スカラー |
拡大量 |
|
9 |
ベクトル |
移動量 |
|
10 |
固有ベクトル |
拡大軸 |
|
11 |
固有値 |
拡大値 |
|
12 |
エルミート行列 |
複素対称変換 |
|
13 |
オイラーの公式 |
オイラーの回転公式 |
本記事を作成するにあたり、貴重な助言を頂いたNS氏に心より感謝いたします。
8. 参照文献
|
[1] |
ケイリー, アーサー (Cayley, Arthur), "行列論 (A Memoir on the Theory of Matrices)," ロンドン王立協会 哲学紀要 (A Philosophical Transactions of the Royal Society of London), vol. 148, pp. 17-37, 1858. |
|
|
[2] |
オイラー, レオンハルト (Euler, Leonhard), "オイラーの無限解析 (Introductio in analysin infinitorum)," オイラー著作全集 (Opera Omnia), vol. 1, no. 8, pp. 92-105, 1748. |
|
|
[3] |
コーシー, オーギュスタン=ルイ (Cauchy, Augustin-Louis), "方程式による惑星運動の永年均差の決定 (Sur l'équation à l'aide de laquelle on détermine les inégalités séculaires des mouvements des planétes)," コーシー著作全集 (Oeuvres Complètes), vol. 2, no. 9, pp. 174-195, 1829. |
|
|
[4] |
コーシー, オーギュスタン=ルイ (Cauchy, Augustin-Louis), "Memoire sur les fonctions qui ne peuvent obtenir que deux valeurs égales et des signes contraires par suite des transpositions operées entre les variables qu'elles renferment," J Ecole Polytech, vol. 10, pp. 29-112, 1815. |
|
|
[5] |
Beltrami, Eugenio, "Sulle funzioni bilineari," Giornale di Matematiche ad Uso degli Studenti Delle Universita, vol. 11, pp. 98-106, 1873. |
|
|
[6] |
Jordan, Camille, "Mémoire sur les formes bilinéaires," Journal de Mathéantiques Purse, Deuxiéme Sérei, vol. 19, pp. 35-54, 1874. |
|
|
[7] |
Hermite, Charles, "Remarque sur un theoreme de M. Cauchy," C.R. Acad. Sci. Paris, vol. 41, pp. 181-183, 1855. |
|
|
[8] |
Sylvester, James Joseph, "On The relation between the minor determinants of linearly equivalent quadratic functions," Philos. Magazine, vol. I, no. 4, p. 295–305, 1851. |
|
|
[9] |
Descartes, René, "La Géométrie," Discours de la méthode, pp. 376-493, 1637. |
|