Here we answer some of the most common questions about the many‑worlds interpretation.
If our universe is a two‑dimensional sheet of paper, a three‑dimensional space can hold an unlimited stack of such sheets. Adding just one more dimension gives plenty of “room” for countless worlds. A natural candidate for that extra dimension is time.
Worlds that exist at different moments are also part of the multitude. We usually picture parallel worlds that coexist at the same instant, but the world ten minutes from now is likewise another world.
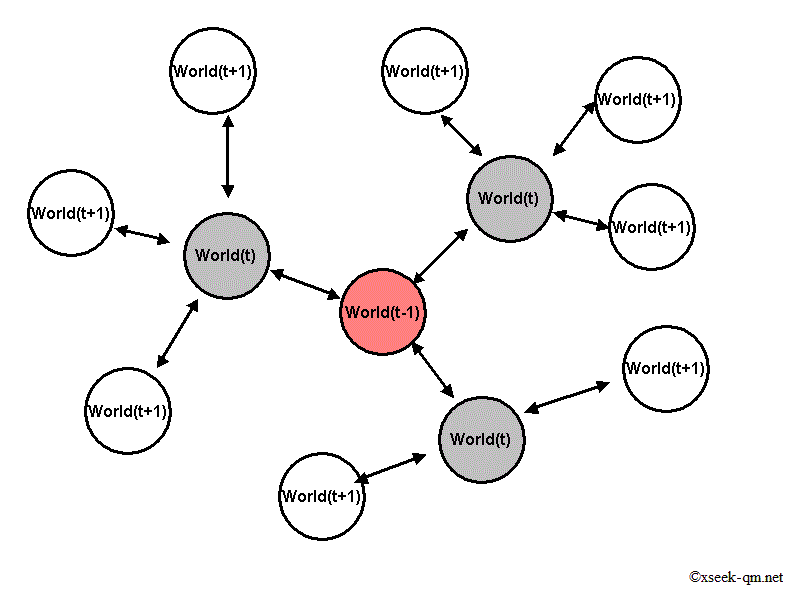
Like distance, time can be measured, yet I believe time does not “exist” in quite the same way distance does. Distinct worlds exist at distinct instants, and we feel time flow by moving from one world to the next.
Even if the universe expands forever, we cannot measure time unless entropy keeps increasing. When entropy finally reaches its maximum, the very phenomenon we call the flow of time may disappear.
Some argue that the number of worlds is infinite; I think it is finite. If an electron’s position could vary by an unlimitedly small amount, each tiny shift would create a new world, giving infinity. But if there are minimal units of length and time, positions cannot vary below those limits, so the total number of distinct worlds must be finite.
A common worry is that energy would grow each time worlds split. Yet we never sum the energies of different times when checking conservation laws, and likewise we need not add the energies of different worlds. Energy is conserved within each separate world.
Many people think other worlds are forever unobservable. I am hopeful that someday a way will be found to detect them.
I feel the path‑integral formulation and the many‑worlds interpretation are closely connected. The difficulty is that quantum mechanics does not select a unique basis, so the state of each world depends on the basis chosen. If no single basis is preferred, the state of a given world becomes ambiguous.
I suspect a unique basis can in fact be chosen. Particle position is a natural candidate, and for spin one might treat “positions” in an internal space as a basis.
© 2005-2014 xseek-qm.net
広告


