The many‑worlds interpretation faces a major challenge: by itself it has not yet
derived Born rule (the rule that an observation’s probability is proportional to the squared modulus of the wave function).
Below I summarize the problem and introduce some ideas that might help derive Born rule.
Born rule is the empirical law that an observation’s probability is proportional to the squared modulus of the wave function. The rule was obtained inductively from experiments, not deduced from theory.
Most textbooks assume Born rule from the outset, so it rarely draws questions, yet I believe it remains a fundamental mystery.
Some papers claim Born rule emerges naturally in the many‑worlds interpretation, but I do not think the matter is so simple.
In his 1957 paper Hugh Everett introduced the concept of measure and stated that it is proportional to the squared modulus of the wave function, yet he did not clearly identify the measure with “the number of worlds.”
If we adopt many‑worlds, it seems natural to speak of probability in terms of “how many worlds.”
If the measure really is proportional to world count, then the measure must itself be a physical entity.
The wave function is also a physical entity that produces interference.
How are these two entities linked? — I believe the key to deriving Born rule lies in that connection.
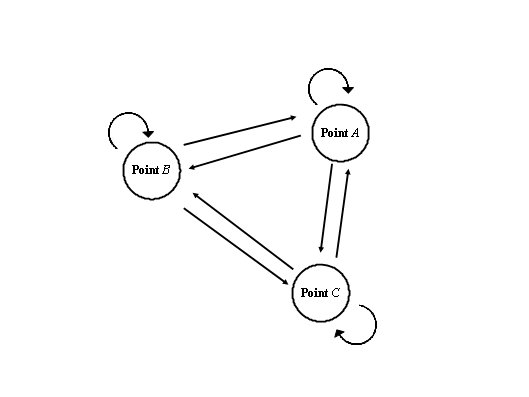
I looked for pairs of quantities in which one is proportional to the square of the other, hoping to map them to the wave function and the measure.
The first three are geometric or mechanical analogies, but I find the fourth — points and paths — most promising. For example, three points yield nine distinct paths among them. If the number of points is N, the total paths are N2, so a “square law” appears naturally.

I hope this article encourages further thought on the problem of probability within the many‑worlds interpretation.
© 2008-2014 xseek-qm.net
広告


