プリンストン大学の学生だったヒュー・エヴェレットは1957年に量子力学の新しい解釈を提唱しました。 その解釈はエヴェレットの多世界解釈と呼ばれています。
エヴェレットの論文の解説記事は次のページにあります。
• エヴェレットの多世界解釈の論文 [2019/2/11]たとえば、箱の中に電子を入れます。量子力学によれば、電子は箱の中で波のように広がっています。 この波のことを波動関数といいます。 人間が箱の中を見れば、電子は箱の中の一点で見つかります。 これを波動関数の崩壊といいます。
電子は、常に粒子で、その存在確率が波にしたがっているだけではないか? そのように考えるのは当然でしょう。しかし、その解釈は正しくありません。 アスペの実験が1982年にその解釈を否定しました。 観測する前の電子は、波のように広がっているのです。
この波動関数の崩壊は、とても不思議な現象です。 たとえば箱の中を、二つの部屋に仕切ります。 すると、電子の波はそれぞれの部屋に存在します。 片方の部屋を見れば、そこには電子はあるかもしれませんし、 ないかもしれません。
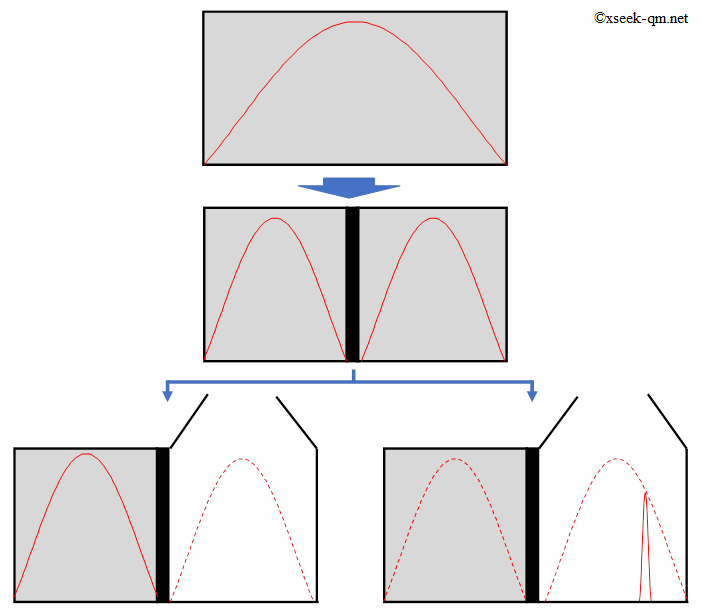
電子がある場所で見つかれば、電子の波動関数はその場所に収縮します。一方、電子が見つからなければ、 電子の波動関数は隣の部屋へ収縮します。 電子を観測した時に、その電子の波動関数が崩壊することはとても不思議です。 しかし、電子を観測しなかった時にも、 その電子の波動関数が崩壊するのはもっと不思議です。
エヴェレットは、「波動関数は崩壊していない」と考えました。 電子を波動関数で表現するのであれば、人間も波動関数で表現すべきだ。 ある人間が電子を観測すると、人間は次のように分かれます。
電子は波のように広がっています。一方、人間も波のように広がっているのです。
私が多世界解釈に初めて触れたのは ブルーバックス「宇宙の運命」でした。 読んだのは10歳くらいのころでしょうか?その本から引用してみましょう。
しかし、SF作家がいうように、偶然が起こるたびに宇宙が二つに分かれると考えてみよう。 もしそれが事実ならたくさんの宇宙が存在しうる。 すこしちがった宇宙、かなり違った宇宙、思いつけるだけの宇宙が存在することになろう。
(中略)
こういう話は実に面白い。 科学理論には、こういう発想を認めるものはあるまいと読者は思うかもしれないが、実は、それがあるのだ。 量子力学の「多世界解釈」とよばれているものがそれだ。 アメリカの物理学者ヒュー・エベリット3世が、 1957年にプリンストン大学の博士論文でこのことを書いた。
(中略)
こんな、幻想的な考えに、反証するのは簡単だろうと思われるかもしれない。 しかし、実はそうではない。 エベリット理論は量子力学の標準的な考え方と、数学的に同じなので、 この二つの違いを見分ける実験は不可能である。
これを初めて読んだ時には、とてもありえそうにないと思いました。 しかし、その後、大学時代に もしかすると正しいかも、と考えるようになってきました。
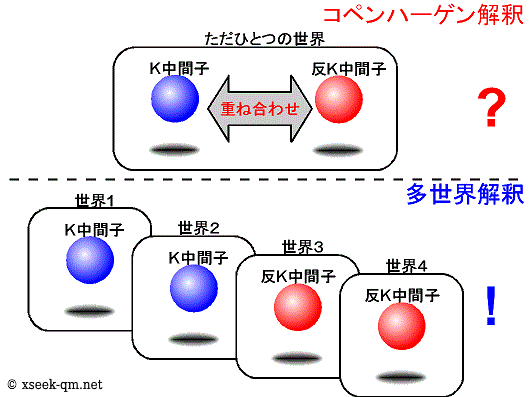
きっかけは、「CP対称性の破れ」の講義での「K中間子ミキシング」の話でした。 このK中間子ミキシングでは、K中間子と反K中間子を重ね合わせた波動関数が出てくるのです。
コペンハーゲン解釈では、物理系は測定されるまで明確な特性をもちません。 そのため、2種類の素粒子の重ね合わせは、測定されるまで明確な特性をもちません。
明らかに異なる2種類の素粒子の重ね合わせというものを理解するためには、 多世界解釈のような考え方がとても有効でした。

そのようなきっかけで、多世界解釈は正しいかもしれないと考えるようになりました。
多世界解釈に関する記述は ブルーバックス「量子の謎をとく」にもあります。 この本で著者はエヴェレットの平行宇宙解釈を紹介しています。 また、デイヴィッド・ドイッチュの量子コンピューターも紹介しています。 しかし、多世界解釈のことが書いてある教科書は全くありませんでした。
「やはり、パラレルワールドを認めるような解釈は、あやしい考え方だからだろうか?」
と考えていましたが、ある日、大学の本屋で多世界解釈に言及している 教科書「量子力学概論」をみつけました。 そこでは、多世界解釈に対して否定的な見解を述べていました。 しかし、私にとっては、教科書が言及したという意味において画期的なことでした。
その後、1994年に多世界解釈を全面的に支持する本、 ブルーバックス「量子力学が語る世界像」が出版されました。 私の知る限り、多世界解釈が極めて好意的に解説された最初の書籍だと思います。
量子力学には観測問題という未解決の問題があります。 これは「波動関数が崩壊し、粒子は確率解釈にしたがい観測される」というものです。 多世界解釈では波動関数は崩壊しないため、この「波動関数の崩壊」問題を解決できます。 そのため、多世界解釈は正しい可能性が高いと考えています。
しかし、現在の多世界解釈の定式化では確率解釈を導出できないため、 その定式化には問題があると考えています。 多世界解釈の定式化は量子力学の数学的構造に依存しているため、 もし多世界解釈を採用するのであれば、その数学的構造にも拡張が必要だと、私は考えています。
© 2002-2013 xseek-qm.net
広告


