ベルの不等式とは、誤解を恐れずに言えば「アリスとボブが出会う確率の上限」を与える不等式のことです。
ベルの不等式は、量子力学の入門書によく出てきます。しかし、その不等式の意味は非常にわかりにくいと思います。 そこで本記事では、ベルの不等式の意味をわかりやすく解説してみようと思います。
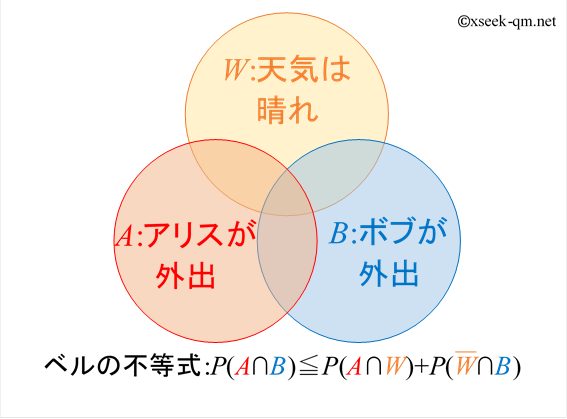
ベルの不等式は次のような不等式です。
(「自分の知っているベルの不等式とちがう」という人は、 後述の「いろいろなベルの不等式」を先に読んでください)
ベルの不等式の意味はとてもわかりにくいです。 その理由の一つは、記号$W$, $A$, $B$ が抽象的な表現だからです。 そこで、記号 $W$, $A$, $B$を、次のような日常的な言葉に置き換えて、ベルの不等式を説明します。
$P(A \cap B)$ は「アリスとボブが同時に外出する確率」を意味します。 $P(A \cap W)$ は「天気が晴れて、アリスが外出する確率」です。また $P(\overline{W} \cap B)$ は「天気が雨で、ボブが外出する確率」です。
ベルの不等式は日常的な言葉で表現すると、次のようになります。
可能なケースを次のように分類します。
上記のケースはベン図で次のように表現できます。

ベルの不等式が成り立つことは次の図でより明らかになります。
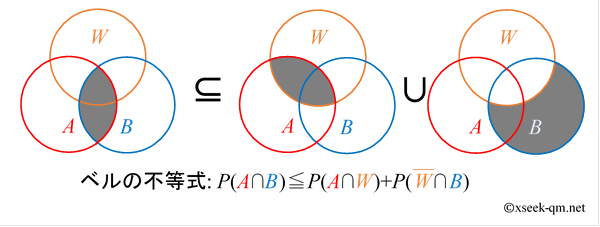
これがベルの不等式です。このように、ベルの不等式の意味はベン図で視覚的にわかります。
さてここで、次のようなケースを考えてみましょう。
ベン図では次のようになります。
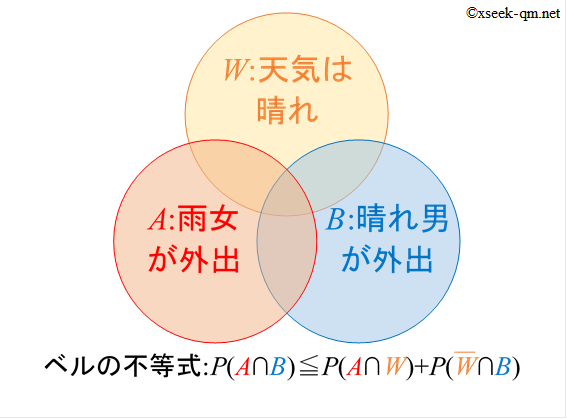
すると、ベルの不等式はさらにくだけた次の文章で表現できます。
この設定で、ベルの不等式に関連する問題を出題したいと思います。
下記を問題の条件とする時、アリスとボブが出会う確率の上限は何%か?
解答は25%です。その解き方を説明します。
念のため、ここで問題が期待している答えを再確認したいと思います。 この問題が期待している解答は「確率」ではありません。「確率の上限」です。 上限ですので「アリスとボブは、なぜか同時に外出しやすい」というケースを考えても構いませんし、 「アリスとボブは、なぜか出会いやすい」というケースを考えても構いません。 この問題は「アリスとボブが出会う確率を最大どこまで高くできるのか?」という問いを出題しています。
条件付き確率を計算するため、この問題を晴れの日の場合と雨の日の場合に場合分けします。 最初に晴れの日のケースを考えましょう。
晴れの確率が50%で、晴れの日にアリスが外出する確率は25%です。 そのため、晴れかつアリスが外出する確率$P(W \cap A)$は $ 50\% \times 25\% = 12.5\%$ です。
一方、晴れの日にボブが外出する確率は75%です。 そのため、晴れかつボブが外出する確率$P(W \cap B)$は $ 50\% \times 75\% = 37.5\%$ です。
晴れの日にアリスとボブが出会うためには、少なくとも両者が外出している必要があります。 そのため晴れかつ二人が出会う確率の上限は、小さいほうの、晴かつアリスが外出する確率$P(W \cap A)$、すなわち12.5%となります。
雨の確率が50%で、雨の日にアリスが外出する確率は75%です。 そのため、雨かつアリスが外出する確率$P(\overline{W} \cap A)$は $ 50\% \times 75\% = 37.5\%$ です。
一方、雨の日にボブが外出する確率は25%です。 そのため、雨かつボブが外出する確率$P(\overline{W} \cap B)$は $ 50\% \times 25\% = 12.5\%$ です。
雨の日にアリスとボブが出会うためには、少なくとも両者が外出している必要があります。 そのため雨かつ二人が出会う確率の上限は、小さいほうの、雨かつボブが外出する確率$P(\overline{W} \cap B)$、すなわち12.5%となります。
晴れの日に出会う確率の上限値(12.5%)と雨の日に出会う確率の上限値(12.5%)を合わせると、二人が出会う確率の上限は25%であることがわかります。
つまり、この問題におけるベルの不等式の右辺は25%となります。
したがって「アリスとボブが出会う確率をどこまで高くできるか?」の答えは25%となります。 この問題の条件を満たしている限り、いかなる手段を用いても、これ以上の確率を得ることはできません。 この結論は、天気を晴れの日と雨の日に場合分けできるかぎり、常に正しい結論です。 しかし、おどろくべきことに、量子力学ではこの不等式の左辺が37.5%となるのです! それについて、次に説明しようと思います。
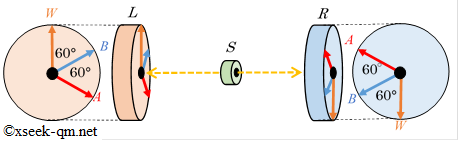
発射装置$S$は一個の電子を左側の観測装置$L$に発射し、もう一個の電子を右側の観測装置$R$に発射します。2個の電子の角運動量の合計を0とします。
観測装置はある一つの方向について電子のスピンを測定できます。 不思議なことに、電子のスピンは必ず$+1/2$か$-1/2$のどちらかとなります。 2個の電子の角運動量の合計が0の場合、、 左側の観測装置$L$が方向$W$で、一個の電子のスピン$+1/2$を得た時、 右側の観測装置$R$が方向$W$で、もう一個の電子のスピン$+1/2$を得る確率は100%になります。
ここから、説明が少し難しくなってきます。 左側の観測装置$L$は方向$A$で一個の電子のスピンを測定します。一方、 右側の観測装置$R$は方向$B$で、もう一個の電子のスピンを測定します。 方向$A$と方向$B$の角度差が$\theta$の場合、 左側の観測装置$L$の方向$A$で$+1/2$だった時に、 右側の観測装置$R$の方向$B$で$+1/2$になる確率は、量子力学では次の式で計算できます。
$$ P(B|A) = \frac{ P(A \cap B)}{P(A)}= \cos^2 \left(\frac{\theta}{2} \right) $$ここで、$P(B|A)$とは、事象$A$が起きた時に、事象$B$が起きる確率です。また、$P(A \cap B)$とは、事象$A$と事象$B$が同時に起こる確率です。 次に例を示します。
方向$A$と方向$B$の角度差は$60^\circ$であるため、 左側の観測装置$L$の方向$A$で$+1/2$だった時に、 右側の観測装置$R$の方向$B$で$+1/2$になる確率は次の式のように75%です。
$$ P(B|A) = \frac{ P(A \cap B)}{P(A)}=\cos^2 \left(\frac{60^\circ}{2} \right) = 75\% $$確率$P(A)$が1/2であるため、両方の測定装置が電子のスピン$+1/2$を同時に得る確率$P(A \cap B)$は、37.5%となります。
$$ P(A \cap B) = 37.5\% $$次に別のケースを考えます。 左側の観測装置$L$は方向$A$で一個の電子のスピンを測定します。一方、 右側の観測装置$R$は方向$W$で、もう一個の電子のスピンを測定します。 方向$A$と方向$W$の角度差は$120^\circ$であるため、 左側の観測装置$L$の方向$A$で$+1/2$だった時に、 右側の観測装置$R$の方向$B$で$+1/2$になる確率は次の式のように25%です。
$$ P(W|A) = \frac{ P(A \cap W)}{P(A)}=\cos^2 \left(\frac{120^\circ}{2} \right) = 25\% $$確率$P(A)$が1/2であるため、両方の測定装置が電子のスピン$+1/2$を同時に得る確率$P(A \cap W)$は、12.5%となります。
$$ P(A \cap W) = 12.5\% $$さらに別のケースを考えます。観測装置$L$は方向$W$の反対方向で電子のスピンを測定します。(今後、$W$の反対方向を意味する新しい記号$\overline{W}$を使います) 一方、観測装置$R$は方向$B$で電子のスピンを測定します。 方向$\overline{W}$と方向$B$の角度差は$120^\circ$なので、 観測装置$L$の方向$\overline{W}$で$+1/2$だった時、観測装置$R$の方向$B$で$+1/2$になる確率は25%になります。
$$ P(B|\overline{W}) = \frac{ P(\overline{W} \cap B)}{P(\overline{W})}=\cos^2 \left(\frac{120^\circ}{2} \right) = 25\% $$$P(\overline{W})$が1/2なので、両方の結果が$+1/2$となる確率は、12.5%となります。
$$ P(\overline{W} \cap B) = 12.5\% $$ここで、ベルの不等式は下記でした。
上記の不等式の左辺は37.5%ですが、右辺の合計は25%となり、ベルの不等式を破っています。
$$ 37.5\% \gt 12.5\% + 12.5\% $$このように観測装置$L$と観測装置$R$の間には、本来ならばありえないような不思議な相関が存在します。 この不思議な相関はEPR相関と呼ばれており、実験で確かめられています。(例えば1982年のアスペの実験で確認された)
EPR相関の不思議さは、いったいどこから生じているのでしょうか? それは「測定結果$A$, $B$は、測定していない結果$W$で場合分けできない」ということだと思います。これは二重スリット実験で、結果を、電子が左のスリットを通ったケースと、電子が右のスリットを通ったケースに場合分けできないという事実に似ています。
ここでは、ベルの不等式が破れる理由を考えてみたいと思います。
前節で、 EPRの不思議さは「$A$と$B$の測定結果が、測定していない$W$の結果で場合分けできないこと」から生じていると述べました。 しかしながら、驚くべきことに「測定していない$W$の結果」を 空間的に分離できるのです。 その解説の前に、電子のスピンの測定方法を説明したいと思います。
電子のスピンを測定するためには、次のようなシュテルン=ゲルラッハの装置を使います。
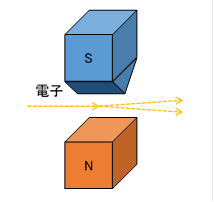
とがったS極と平坦なN極の間には不均一な磁場が生じています。 磁場の強さは、S極に近づくほど強くなります。 その不均一な磁場を通る電子ビームは二つの軌道に分かれます。 その軌道で、電子のスピンの方向がわかります。 元のスピンがどの方向を向いていたとしても、 必ず磁石の方向に対し、二つの軌道に分かれます。
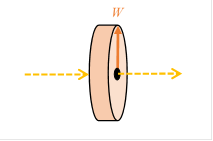
このシュテルン=ゲルラッハの装置を組み合わせ次のような装置を作ります。
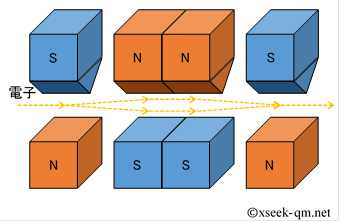
上記の装置では、一度分岐した電子ビームが再び合流しています。 後のために、上記の装置を次の図で略記しようと思います。
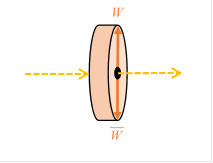
その装置に、壁$C$を置きます。
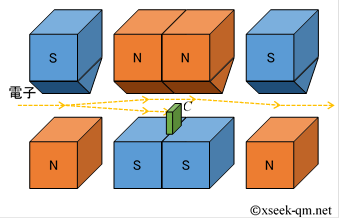
下側の軌道がさえぎられるので、どちらの軌道を通ったか分かります。 後のために、上記の装置を次の図で略記します。
これらの装置を使い次の思考実験を行います。
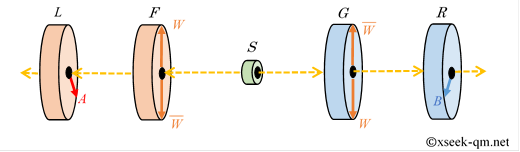
電子ビームは装置$F$と装置$G$で、軌道$W$と軌道$\overline{W}$に分離され、再び統合されますが、 それでも装置$L$と装置$R$の間でEPR相関が起きます。
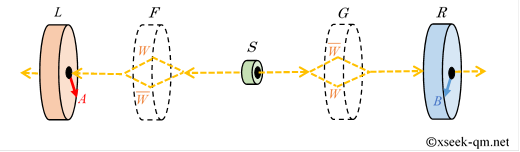
これはとても不思議な結果です。 なぜなら、電子ビームが軌道$W$と軌道$\overline{W}$に分離されていた時点では、 電子ビームはケース$W$とケース$\overline{W}$に場合分けできているからです。 場合分けできるならば、ベルの不等式が成り立つはずです。 なぜベルの不等式が破れるのでしょうか?
確かに、電子ビームが軌道$W$と$\overline{W}$に分離している時点では、ベルの不等式は成立しています。 分離した電子ビームが再び合流することで干渉しベルの不等式を破るのです。 この相関は、二つの電子が一つの量子状態を構成していることを意味します。 したがって、ベルの不等式を破る理由は次のようにまとめられます。
実は、ベルの不等式には、いくつか種類があります。それぞれのベルの不等式について説明します。
アイルランドの物理学者ベルは1964年に次の不等式を提案しました。
関数 $C(A,B)$ は事象 $A$ と事象 $B$ の相関の強さを意味します。 しかし、その不等式の意味は非常にわかりにくいと思います。 米国の物理学者クラウザーらは1969年にベルの不等式を改良し、次の不等式を提案しました。
この不等式の意味も、わかりにくいと思います。 ハンガリーの物理学者ウィグナーは1970年にベルの不等式を改良し、次の不等式を提案しました。
物理学者サクライは1994年に出版された教科書「現代の量子力学」で、 上記の不等式をベルの不等式として紹介しています。 ここで、関数 $P(A+;B+)$ は、次のEPR実験で、左側の観測装置$L$が方向 $A$で電子のスピン$+1/2$を観測し、 右側の観測装置$R$が方向$B$で電子のスピン$+1/2$を観測する確率です。
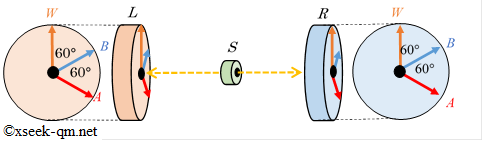
ベルの不等式(1964年)とCHSH不等式(1969年)は相関の強さの不等式でした。 一方、ウィグナー=デスパーニアの不等式(1970年)は確率の不等式です。 そのため、これまでよりも不等式の意味を理解しやすくなりました。 しかし、まだ不等式の意味はわかりにくいと思います。 その理由は、左側の観測装置$L$の方向$A$,$B$,$W$と右側の観測装置$R$の方向$A$,$B$,$W$が同じ方向だからです。 私は右側の観測装置$R$の方向を次のように180度回転させた方が、わかりやすいと思います。 なぜならば、左側の観測装置$L$と右側の観測装置$R$には逆の相関があるからです。

ベルの不等式は、上記のEPR実験に基づいて、次のように集合で表現した方が、不等式の意味がわかりやすいと思います。
$$ P(A \cap B) \leqq P(A \cap W)+P(\overline{W} \cap B) $$本記事では、上記の不等式をベルの不等式として説明しました。 ベルの不等式はベン図で次のように表現できます。
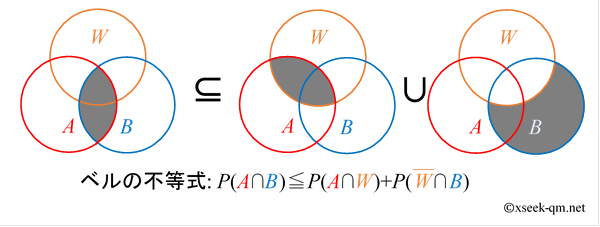
上記のベン図を見れば、ベルの不等式の意味が、はっきりわかると思います。実際、 フランスの物理学者デスパーニアも1979年にベルの不等式をベン図で説明しました。
ベルの不等式は、天気を晴れと雨に場合分けできるならば正しいです。 しかし、量子力学の世界では、天気を観測しないとき、天気を晴れと雨に場合分けできないのでした。
アリスがボブと出会ったとき、二人にその日の天気をたずねたら、どのような答えが返ってくるのでしょうか? 実は、量子の世界では不思議なことに、観測しない場合、天気が晴れなのか雨なのかは不確定なままなのです。
© 2002-2018 xseek-qm.net
広告


