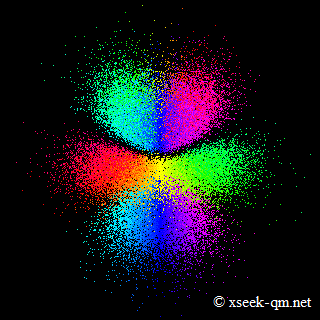
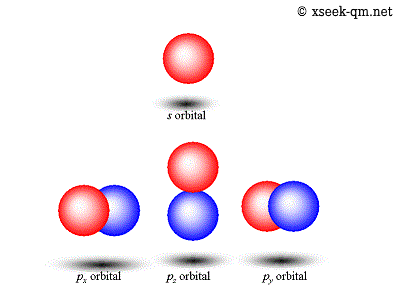
ボーアの原子模型によれば、原子核のまわりを電子が回転しています。 原子軌道は球面調和関数で表現できます。 しかし、次のような原子軌道の絵を見ても、公転には見えません。
上の絵の2段目に、赤の玉と青の玉がつながった形が見えます。 2段目の形は角運動量をもっているため、回転している電子を表現しているはずです。 しかし、回転軸を見つけることができません。
一方、 数理美術科学館様 の 「位相で見る波動関数」のページ では、次のような方法で、波動関数を表現しています。
この方法で、原子核まわりの電子の回転をアニメーションで表示できます。
これをJavaScriptでアニメーション表示できないかと考えました。 そのアニメーションを次の節でお見せします。
水素原子で回転する4f軌道の電子の波動関数のGIF(ジフ)アニメーションを次のページで参照できます。
Youtubeでも公開しています。
次のようなステップで動画をつくっています。
そうすると、位相を変化させるだけで、回転しているように見えるわけです。
水素原子で回転する電子の波動関数のJavaScriptアニメーションは次のページのとおりです。
初期の状態は(n,l,m)=(4,3,1)の状態です。(n:主量子数、l:方位量子数、m:磁気量子数)
「State」ボタンを押せば、状態(1,0,0),(2,1,1),(3,2,1),(3,2,2),(4,3,1) のひとつをえらべます。 (n,l,m)=(1,0,0)の状態は回転していません。 位相が全体的に変わります。
初期の点の数は51200個です。 マシンパワーに余裕がないようでしたら、「Number」ボタンをおして点の数を減らしてみてください。
© 2012-2013 xseek-qm.net
広告


