ベルの宇宙船パラドックスを紹介します。
物理学者のエドモンド・デューアンとマイケル・ベランは「二台のロケットのパラドックス」を1959年に提示しました。 物理学者のジョン・スチュアート・ベルが1987年に紹介したことから「ベルの宇宙船パラドックス」と呼ばれています。
一般的に、この思考実験は二台の宇宙船で説明します。 しかし、光速があまりにも速いため、その思考実験を想像することは困難です。 そこで、光速を秒速30ミリメートルと仮定します。
今、机の上に一匹のチョウの幼虫がいます。 全長は30ミリメートルです。
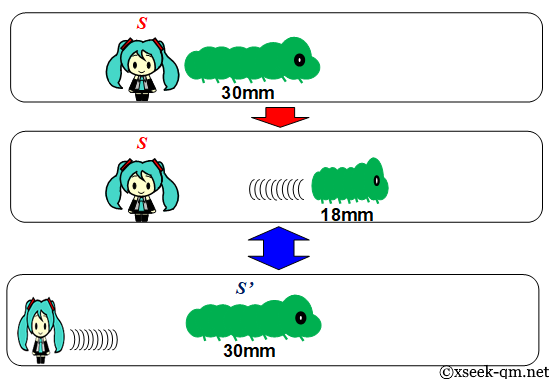
その幼虫が10秒間加速しました。 その速度は秒速24ミリメートルになりました。 幼虫の全長は何ミリメートルになるでしょうか?
ローレンツ収縮の公式は次のとおりです。
$$ L = L_0 \sqrt{1-\frac{v^2}{c^2}} $$変数は L0 = 30mm、v = 24mm/s、c = 30mm/s です。 幼虫の全長を次のように計算します。
$$ L = 30 \sqrt{1-\frac{24^2}{30^2}} = 18 $$したがって、L = 18mm となります。 ローレンツ収縮により幼虫の全長は収縮します。
しかし、幼虫の運動系 S ' では、幼虫の全長は30ミリメートルです。
次に二匹のアリを机に置きます。 二匹のアリの間の長さは30ミリメートルです。
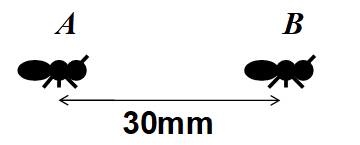
その二匹のアリが10秒間加速しました。 その二匹のアリは静止系 S で同じ時刻に加速を開始しました。 そして、その二匹のアリは静止系 S で同じ時刻に加速を終了しました。 その二匹のアリの速度は秒速24ミリメートルになりました。 その二匹のアリの間の長さは静止系 S でいくらでしょうか?
ある人は、ローレンツ収縮によって、二匹のアリの間の距離が 収縮するとお考えになるかもしれません。 しかし、二匹のアリの間の距離は静止系 S で収縮しません。 なぜなら、二匹のアリの加速の終了時刻が静止系 S で同じだからです。
加速度を適度に調整すれば、アリは静止系 S で10秒間、 加速度 a=2.4mm/s2 で加速可能です。 静止系 S で時刻0秒のアリAの位置を0ミリメートルとします。 すると、時刻 t 秒のアリAの位置 x(t) は、次の式で表現できます。
$$ x(t) = \frac{1}{2} at^2 $$上記の式を計算し、10秒後のアリAの位置を得ることができます。 それは、120 ミリメートルです。 一方、静止系 S で時刻0秒のアリBの位置を30 ミリメートルとすれば、 時刻 t 秒のアリBの位置 y(t) は、次の式で表現できます。
$$ y(t) = 30 + \frac{1}{2} at^2 $$上記の式を計算し、10秒後のアリBの位置を得ることができます。 それは、150 ミリメートルです。 したがって、10秒後の二匹のアリの間隔は30 ミリメートルとなります。 10秒後の二匹のアリの速度は24mm/sです。その後、アリはその速度を維持します。 そのため、静止系 S でのアリの間隔は、常に30 ミリメートルです。
次に、その二匹のアリに糸を取りつけます。 二匹のアリが加速するとき、なにが起きるでしょうか?
二匹のアリが加速するとき、糸が切れます。 ある人は、この結果を信じないかもしれません。 なぜなら、糸の長さが変わらないからです。 なぜ糸が切れるのでしょうか?
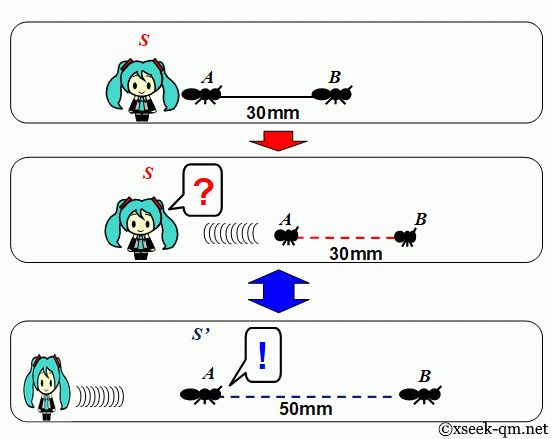
アリ A の運動系 S ' を考えます。 アリ A が加速すると、アリ A の同時線が変わります。 そのため、アリBはアリAよりも早く加速を完了します。 このとき、アリBの速度はアリAの速度よりも速いです。 そのため、アリAが加速を完了するときに、 アリAとアリBの間隔はもっと長くなります。 アリ A の運動系 S ' で、間隔は50ミリメートルになります。そのため、糸が切れるのです。
静止系 S で糸の長さが変わらないため、静止系 S において、これは不思議な現象です。 なぜ糸が切れるのでしょうか? 実は、静止系 S での分子間力の距離が短くなったため、糸が切れるのです。
ローレンツ収縮をミンコフスキー空間で説明します。
ローレンツ変換は次のとおりです。
$$ x' = \gamma(x - \beta ct) $$ $$ ct' = \gamma(ct-\beta x) $$ここで変数 γ と β は次のように定義しました。
$$ \gamma = \frac{1}{\sqrt{1-\beta^2} $$ $$ \beta = \frac{v}{c} $$変数は、v = 24mm/s、c = 30mm/s です。 ローレンツ変換を次のように計算します。
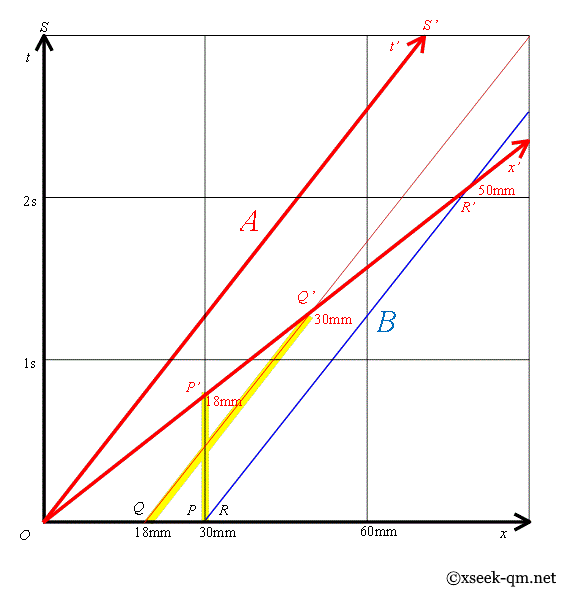
$$ x' = \frac{5}{3}(x-\frac{4}{5} ct) $$ $$ ct' = \frac{5}{3}(ct-\frac{4}{5} x) $$アリ Aの世界線は線Aです。 アリ Bの世界線は線Bです。 静止系 S の二匹のアリの間の距離は線分 OR です。 運動系 S ' の二匹のアリの間の距離は線分 OR ' です。
静止系 S の幼虫の全長は線分 OQ です。 運動系 S ' の幼虫の全長は線分 OQ ' です。 私は線分 PP ' と線分 QQ ' のクロス構造に注目したいと思います。 そのクロス構造がローレンツ変換の本質的な構造だと推測します。
アリから見た加速度αが一定のアリの軌跡x(t)は次の式で表現できます。
$$ x(t) = \frac{c^2}{\alpha}\sqrt{1+ \Big(\frac{\alpha t}{c}\Big)^2}-\frac{c^2}{\alpha} $$上記の式では初期条件を時刻t=0のときx=0としましたが、 初期条件を変更し時刻t=0のときx=c²/αにすると、式は次のように少し簡単になります。
$$ x(t) = \frac{c^2}{\alpha}\sqrt{1+ \Big(\frac{\alpha t}{c}\Big)^2} $$加速度αが2.4m/s²の場合のアリの軌跡は次のグラフの青い実線です。 黒い破線は軌跡の漸近線です。
このアリの同時線は常に原点(x,t)=(0,0)を通ります。 そのため、アリから見ると原点の位置は不変であり、原点の時刻も経過しません。 また原点を出発した光は決してアリに追いつかないため、原点はアリから見て黒い壁のように見えます。 この黒い壁はブラックウォールと呼ばれています。ブラックウォールとアリBの中間地点にいる別のアリAが 同じ加速度で進む場合、「ベルの宇宙船パラドックス」で説明したように二匹のアリの距離は、アリから見て徐々に開きます。 アリから見て距離が変わらないようにするにはどうすればよいでしょうか?そのためにはアリAはアリBよりも大きな加速度で進む必要があります。アリBとブラックウォールの間の距離がアリAとブラックウォールまでの距離の半分の場合、アリBはアリAの二倍の加速度で進む必要があります。加速度α'=2αのアリBの軌跡は次の数式で表現できます。
$$ x(t) = \frac{c^2}{2\alpha}\sqrt{1+ \Big(\frac{2\alpha t}{c}\Big)^2} $$アリAとアリBの軌跡は次のグラフの赤い実線と青い実線です。 黒い破線は軌跡の漸近線です。緑色の実線は同時線です。
このような座標はリンドラー座標と呼ばれています。
静止系から見ると、アリはブラックウォールから離れていきますが、アリから見ると、 「ブラックウォールからアリまでの距離」の増大率と 「アリから見た静止系の距離のローレンツ収縮」の収縮率がぴったり一致するため、 アリから見たブラックウォールまでの距離は常に一定となります。
© 2002, 2015 xseek-qm.net
広告


