等価原理とは、加速による慣性力と重力は区別できないというアイデアです。
このページでは、重力の原因を考えてみたいと思います。

アインシュタインは、1907年に特許局で「生涯最高のアイデア」である等価原理をひらめきました。 等価原理とは、次の二つの状態が局所的に等価であるという原理です。
たとえば、地上にエレベータの箱を置き、中に人を入れます。 そして、その人に、エレベータの箱は宇宙に浮いている、と伝えてみましょう。
その人はエレベータの床に押しつけられています。 このため、その人は、エレベータの箱は上向きに加速している、と推論するはずです。
つまり、等価原理によれば、私たちの周りの空間が、 重力加速度9.8[m/s2]で地球に向かって落ちていると解釈できます。
等価原理の視点で重力が発生する仕組みを考えてみましょう。 重力加速度をニュートンの重力方程式で表現すると次のようになります。
ここで、g, G, M, R は次のとおりです。
| 重力加速度 g | 9.8[m/s2] |
| 重力定数 G | 6.7×10-11[m3/s2kg] |
| 地球の質量 M | 6.0×1024[kg] |
| 地球の半径 R | 6400[km] |
両辺に4πR2 をかけると次のようになります。
等価原理の視点では、地球が、半径 R の球殻で 4πR2×9.8[m3] の体積を加速的に吸い込んでいると解釈できます。 一方、右辺は4π×6.7×10-11×M [m3] の体積を 加速的に吸い込んでいると解釈できます。
私たちの空間は3次元であるため、この加速的な吸い込みは距離の逆2乗に比例して減衰します。
この等価原理の数学的表現をアインシュタインは8年間考え続けました。 そしてついにアインシュタインは時空の曲がり(時空歪曲)で表現できることを見抜きました。 アインシュタインはまさに天才だと思います。こうして1915年に一般相対性理論が完成しました。
時空歪曲の様子を次の図で説明します。
青の線は、無重力の状態で静止している物体を表しています。 赤の線は、重力場の中で、右側に落ちている物体を表しています。
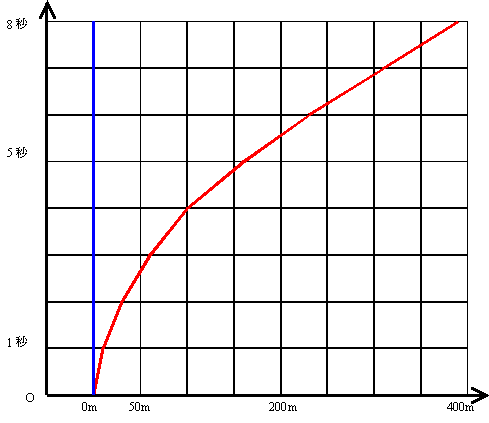
運動する物体が無重力状態の空間に静止していると解釈するならば、 運動する物体の軌跡は時空の曲がりと解釈できます。
一般相対性理論を説明するために、空間を表現した、湾曲したシートがよく使われます。 しかし、実際には、空間ではなく時空が歪曲しているのです。
時空歪曲と物質の関係を探るため、次のアインシュタインの重力方程式を見てみましょう。
左辺のGμνが幾何学的な量です。 右辺のTμνが物質的な量です。 式より、物質が時空を曲げていることがわかります。 ここで、アインシュタインの1936年の著書「物理と実在」から引用します。
私たちが知る限りにおいて、(一般相対性理論は)、天体力学における経験を表現するには十分です。 しかし、それを建物にたとえてみると、 ある一方の翼(方程式の左側)は上質な大理石で造られており、 もう一方の翼(方程式の右側)は粗末な木材で造られています。 実際の所、物質の現象論的な表現は、物質のすべての既知の特性に正当性を与える表現の 粗削りな代替物にすぎません。
この「ある一方の翼は上質な大理石」「もう一方の翼は粗末な木材」という表現は 象徴的だと思います。おそらく、右辺も幾何学的な量で書くべきなのでしょう。 物質も幾何学的原理にもとづいて表現すべきなのだと思います。
重力の発生原因はなんでしょうか? アインシュタインの重力方程式は、物質と時空歪曲の関係を教えてくれます。 しかし、物質が時空を曲げる原因は教えてくれません。 物質は、いったいどのようにして時空を曲げているのでしょうか?
数学者のクリフォードは1870年にケンブリッジ哲学会への論文で次のように述べました。 ( 「超ひも理論入門〈下〉」からの引用です)
- 空間の小さな領域は、実際には、平均すれば平らな表面上の小さな丘に性質が似ている。 すなわち幾何学の通常の法則はそこでは役に立たない。
- 曲がっている、もしくはゆがんでいるこの特性は空間の一部から別の部分へ波のように連続的に伝わる。
- 空間の曲率の変動こそ、私たちが物体の運動と呼ぶ現象で実際に起きていることである。
つまり、物質とは歪曲した空間なのかもしれません。 物質が歪曲した空間であれば、左辺も右辺も歪曲した空間となるため、 重力の発生原因を説明できるかもしれません。 最終的な結論として、重力の発生原因は謎です。 あなたも、この謎を解くことにチャレンジしてみませんか?
© 2013-2014 xseek-qm.net
広告


