本サイトでは、量子論の入口をご案内したいと思います。 あまり物理学に慣れ親しんでいない方々にも理解いただけるように記事を書きたいと考えています。 量子論に興味をもっていただけたら幸いです。
最初に、量子力学の二重スリット実験を紹介したいと思います。

上の図では、電子が壁に向かって飛んでいます。 その壁には二個のすきまがあります。 その電子は、壁にあたるか、あるいは、すきまをとおります。 すきまをとおった電子は、もうひとつの壁にあたります。 たくさんの電子がすきまをとおると、なにが起こるでしょうか? 次の図のように、いくつかの電子が壁にあたります。
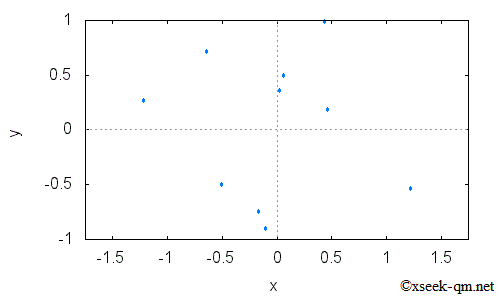
壁にあたる電子の個数を増やすと、上記の図は次の図に変化します。
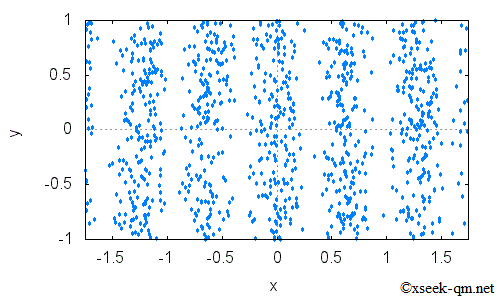
上記の図には、しま模様があります。 電子の分布は次の図のとおりです。
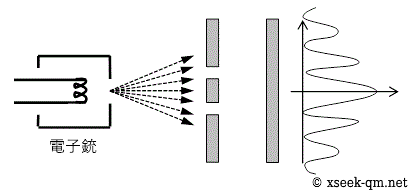
なにが、このしま模様を作ったのでしょうか? 実は、電子は波の性質をもっています。 二個のすきまをとおった波は強め合ったり弱めあったりします。 この現象は干渉と呼ばれています。 波の干渉が、そのしま模様を作りました。 この実験は「二重スリット実験」と呼ばれています。 私は、この結果をとても不思議だと思います。 電子は一個ずつ、すきまをとおります。 なぜ干渉による、しま模様を見ることができるのでしょうか?
電子の波は次の関数で表現します。
この関数は波動関数と呼ばれ、プサイ・エックスと発音されます。 変数xは電子の位置を記述する実数です。 波動関数は、複素数の関数です。 波動関数は、電子の状態を記述します。
二重スリット実験で、電子には二つの経路があります。 一番目の経路は、右のすきまをとおる経路です。 二番目の経路は、左のすきまをとおる経路です。 右のすきまをとおった波の波動関数を ΨR (x ) と表現します。 左のすきまをとおった波の波動関数を ΨL (x ) と表現します。 これらの二つの波動関数 ΨR (x )とΨL (x ) を足し算します。
この足し算によって、干渉が発生します。 これを「重ね合わせの原理」といいます。 電子の観測確率P(x )は、波動関数の絶対値の2乗となります。
なぜ、電子の観測確率は、波動関数の絶対値の2乗なのでしょうか?
物理学者のファインマンは1965年に 教科書「ファインマン物理学〈5〉量子力学」で次のように述べています。
いまでもまだ、次のような質問をしようとする人がいるかもしれない。 "どうしてそんなことになるのか。法則の背後にかくされているからくりは何か" と。
法則の背後のからくりなどを発見した人は、これまでひとりもいない。 たったいま "説明" した以上のことを "説明" できる人はいない。 だれも、いまの状況をより深遠に表現してくれるひとはない。 上に述べた結果を導きうるようなより基本的な機構についてのアイディアを、 われわれはもっていないのである。
つまり、仕組みは「わからない」のです。 教科書「ゲージ理論入門」より 1951年のアインシュタインの言葉も引用します。
50年間も意識して問題をあたためながら、 私はまだ " 光の量子とは何か " という問題の答えに、 少しも近づいておりません。 もちろん今日では、誰もが答えを知っていると思っています。 しかしそれはみずからを欺いているにすぎません。
このサイトでは、量子論の不思議を一緒に考えていければいいなと、思っています。
© 2002-2014 xseek-qm.net
広告


