The Born rule in quantum mechanics tells us that an electron's wave function determines the probability of observing that electron. Specifically, the probability of detecting a particle like an electron is proportional to the square of the magnitude of its wave function. This page explains how to derive the Born rule in quantum mechanics.
In general, the Born rule is regarded as a fundamental principle of quantum mechanics. A fundamental principle is an assumption that requires no further justification. Consequently, most physicists do not attempt to derive the Born rule from deeper principles. So why am I seeking such a derivation?
I asked myself, "Is the Born rule truly a fundamental principle?" According to the rule, the probability of observing an electron is proportional to the square of the modulus of its wave function. I believe, however, that probabilities should be derived from Laplace's probability theory. The next section reviews Laplace's approach to calculating probabilities.
Laplace's probability theory provides a method for calculating probabilities. The French mathematician Pierre-Simon Laplace introduced this theory in 1814. For example, imagine a bag containing three red balls and two blue balls.
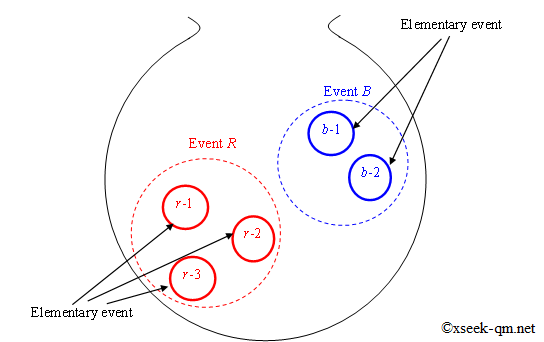
If you reach into the bag and draw a ball, what is the probability of drawing a red ball? Laplace's theory calculates this by considering events and elementary events. An elementary event cannot be subdivided further. For instance, the event R, drawing a red ball, consists of these three elementary events:
Each "drawing the red ball r-1" event is elementary because it cannot be subdivided. In Laplace's theory, the probability of an event is the number of favorable elementary events divided by the total number of elementary events. For example, the probability of event R is 3/5, since there are three favorable outcomes out of five possible outcomes.
The Born rule's method of calculating probability differs fundamentally from Laplace's approach. Why, in the Born rule, do we square the wave function's magnitude instead of using the simple ratio of elementary events? We call this the "probability problem of quantum mechanics." In this page, we will explore solutions to this problem using the many-worlds interpretation and probability theory. The next section introduces the many-worlds interpretation.
In the many-worlds interpretation, every aspect of reality is described by a universal wave function. Different people imagine this "wave function of the universe" differently. To conceptualize it, we start with the wave function of a single particle and then extend the idea step by step.
To address the probability problem, we consider the wave function of multiple particles.
If the position of the k-th elementary particle is \begin{align*} r_k = (x_k, y_k, z_k), \end{align*} then the multi-particle wave function is:
\begin{align*}
\Psi = \Psi(r_1, r_2, r_3, \dots, r_n)
\end{align*}
This wave function describes the positions of n elementary particles. By varying these positions, one can represent any possible universe configuration.
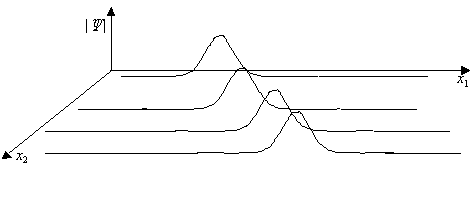
Each point in the multi-particle wave function corresponds to a different world. The probability distribution P is given by:
\begin{align*}
P(r_1, r_2, r_3, \dots, r_n) = \bigl|\Psi(r_1, r_2, r_3, \dots, r_n)\bigr|^2
\end{align*}
The following paper derives the Born rule using the many-worlds interpretation combined with probability theory.
A key concept in this derivation is the hierarchical universe. For more details on the hierarchical universe, see the paper.
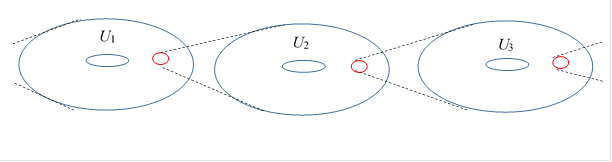
Below is an overview of the hierarchical universe.
The hierarchical universe is a nested set of universes.
Within our universe, each particle has an associated wave function. I propose there is a smaller universe whose radius equals the magnitude of that wave function.
Within that smaller universe, there is also a particle with its own wave function, giving rise to an even smaller nested universe whose radius equals the magnitude of its wave function.
Conversely, the wave function that defines the radius of our universe describes a particle that exists in an even larger universe.
In this way, our universe and the smaller universe are linked by the corresponding wave function.
© 2012-2015 xseek-qm.net
広告


