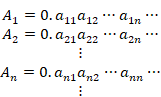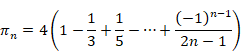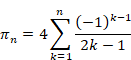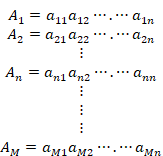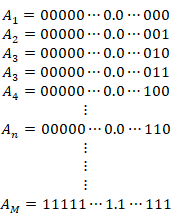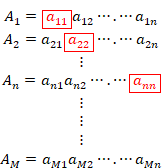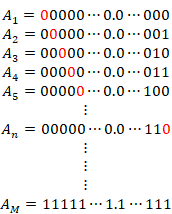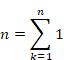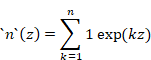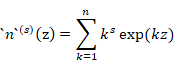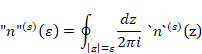Consideration of Cantor's diagonal argument for actual infinity and potential infinity

 

Home  >  Quantum mechanics  >  Actual infinity and potential infinity

 

2020/3/27

Published 2015/6/26

Koji Sugiyama

 

The diagonal argument is a method to prove that a set of real numbers is a set we cannot count.

In this article, we consider Cantor's diagonal argument for actual infinity and potential infinity.

 

The actual infinity is infinity that does not change. It has been completed from the beginning. On the other hand, potential infinity is infinity that changes. It has never been completed. For modern mathematics, the actual infinity is an axiom. Therefore, the claim that "actual infinity does not exist" cannot obtain consent. Then, we separate mathematics to actual infinite mathematics and potential infinite mathematics in this article.

 

We express a set of n natural numbers as a finite set . In addition, we express a set of n-digit decimal numbers as a finite set . We express decimal numbers as binary numbers. The number of elements in the set is 2ⁿ. Therefore, we express the finite set  of decimal numbers those are greater than or equal to zero and less than one at the following table.

 

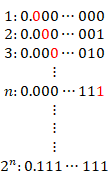
The number of lines of the table is 2ⁿ.

 

The finite set  of decimal numbers cannot be put into one-to-one correspondence with the finite set .of natural numbers, if we apply the diagonal argument to this table, because the number 2ⁿ of elements in the finite set of decimal numbers is greater than the number n of elements in the finite set  of natural numbers.

 

 

However, the finite set  of decimal numbers can be put into one-to-one correspondence with the finite set .that has M = 2ⁿ natural numbers.

 

We construct real numbers by changing the number of digits to the potential infinity.

 

The set of real numbers will be countable set. However, in modern mathematics, decimal numbers those have the potential infinite digits are not real numbers, because real numbers have actual infinite digits from the beginning. Then, we separate mathematics to actual infinite mathematics and potential infinite mathematics, and we define decimal numbers those have the potential infinite digits as real numbers of potential infinite mathematics.

 

In this article, we prove that the set of real numbers of actual infinite mathematics is not a countable set, and we prove that the set of real numbers of potential infinite mathematics is a countable set.

 

 

Table of contents

1.     Introduction. 3

1.1.      History. 3

2.     Actual infinite mathematics. 4

2.1.      Basic concepts. 4

2.1.1.      Set of natural numbers. 4

2.1.2.      Set of rational numbers. 4

2.1.3.      Sequence. 4

2.1.4.      Real numbers defined by the Cauchy sequence. 5

2.1.5.      Limit 5

2.1.6.      Set of real numbers. 6

2.1.7.      Cardinal number 6

2.1.8.      Countable set 6

2.2.      Applied concepts. 7

2.2.1.      Pi defined by series. 7

2.2.2.      Pi defined by an infinite decimal number 7

2.2.3.      Real numbers defined by an infinite decimal number 7

2.2.4.      One defined by an infinite decimal number 7

2.3.      Cantor's diagonal argument 8

3.     Potential infinite mathematics. 10

3.1.      Basic concepts. 10

3.1.1.      Finite set of natural numbers. 10

3.1.2.      Finite set of rational numbers. 10

3.1.3.      Finite sequence. 11

3.1.4.      Real numbers defined by Cauchy finite sequence. 11

3.1.5.      Finite set of real numbers. 12

3.1.6.      Zero. 12

3.1.7.      Infinity. 13

3.1.8.      Limit 13

3.1.9.      Set of natural numbers. 14

3.1.10.    Set of rational numbers. 14

3.1.11.    Sequence. 15

3.1.12.    Set of real numbers. 15

3.1.13.    Countable set 16

3.2.      Applied concepts. 16

3.2.1.      Pi defined by sequence. 16

3.2.2.      Pi defined by a finite decimal 17

3.2.3.      The real number defined by the potential infinite decimal number 18

3.2.4.      One defined by the potential infinite decimal number 19

3.2.5.      Set of real numbers. 20

3.3.      Cantor's diagonal argument 20

4.     Consideration. 23

5.     Conclusion. 23

6.     Supplement 23

6.1.      The real number defined by Dedekind cut 23

6.2.      The real number defined by the Cauchy sequence. 24

6.3.      Peano axioms. 24

6.4.      Russell's axiom of infinity. 25

6.5.      Zermelo's axiom of choice. 25

7.     Appendix. 27

7.1.      Quantum number theory. 27

8.     Acknowledgment 28

9.     References. 29

 

 

We consider Cantor's diagonal argument for actual infinity and potential infinity.

 

The actual infinity is infinity that does not change. It has been completed from the beginning. On the other hand, potential infinity is infinity that changes. It has never been completed.

 

In this article, we prove that the set of real numbers of actual infinite mathematics is not a countable set, and we prove that the set of real numbers of potential infinite mathematics is a countable set.

 

Historically, the following mathematicians supported the actual infinity.

- Dedekind (1831-1916)

- Cantor (1845-1918)

- Hilbert (1852-1943)

- Russell (1872-1970)

- Gödel (1906-1978)

 

Cantor wrote the following in a letter to G. Eneström in 1886.

 

There are substantial differences in terms of the potential and actual infinity. The former is variable finite, and it is growing over all finite limit beyond size. The latter is a self-fixed constant, but it is quantum lying beyond all finite sizes. Despite the differences, one is unfortunately too often confused to think that they change.

 

On the other hand, the following mathematicians have objected to the actual infinity.

- Gauss (1777-1855)

- Cauchy (1789-1857)

- Kronecker (1823-1891)

- Poincare (1854-1912)

- Wyle (1885-1955)

 

Gauss wrote the following in a letter to Heinrich Schumacher in 1831.

 

I protest against the use of infinite magnitude as something completed, which is never permissible in mathematics. Infinity is merely a way of speaking, the true meaning being a limit which certain ratios approach indefinitely close, while others are permitted to increase without restriction.

 

In addition, Poincare wrote the following in the work that was published in 1913.

 

There is no actual (given complete) infinity. The Cantorians have forgotten this, and they have fallen into contradiction. It is true that Cantorism has been of service, but this was when applied to a real problem whose terms were precisely defined, and then we could advance without fear.

 

However, in modern mathematics, the actual infinity is an axiom. Therefore, we cannot deny the actual infinity in the current mathematics. Then, we do not deny the actual infinity, but separate mathematics to one mathematics that assumes the actual infinity and the other mathematics that assumes the potential infinity. Therefore, in this article, we propose to separate the current mathematics the following two.

 

- Actual infinite mathematics

- Potential infinite mathematics

 

 

Actual infinite mathematics is mathematics that considers the actual infinity.

 

We define the set of natural numbers as follows.

(The set of natural numbers)

We abbreviate the above set as follows.

The set of natural numbers contains all natural numbers.

 

We define the set of rational numbers as follows.

(The set of rational numbers)

The set of rational numbers contains all rational numbers

 

We call the numbered subset of rational numbers the sequence.

(The sequence)

We abbreviate the above sequence as follows.

 

Cauchy defined the following Cauchy sequence in 1821.

(Cauchy sequence)

 

We read the character ε as epsilon. It means the error of Cauchy sequence.

Cauchy sequence {a_n} is a sequence in which the value hardly changes in the range of the error ε for a sufficiently large n.

 

Cantor defined a real number a by the Cauchy sequence a_n in 1872.

(Real numbers)

The real number a is a constant that does not depend on the error ε.

 

Cantor called real numbers the continuum.

 

We define the limit as follows.

(Limit)

 

We shortly express the above limit as follows.

(Limit)

We abbreviate the above formula as follows.

(Limit)

 

We define the set of real numbers  by a real number a as follows.

(Set of real numbers)

The set of real numbers contains all real numbers.

 

Cantor introduced a cardinal number as a general concept of the number of elements of a set.

 

We show the cardinal number of the set of natural numbers as follows.

We read the symbol  as aleph-zero. The symbol  is the first letter of the Hebrew characters.

 

We show the cardinal number of the set of real numbers as follows.

 

The countable set is the following set.

 

- The set we can number with natural numbers to all elements.

 

Georg Cantor proposed the countable sets in 1891.

 

We show examples of countable sets as follows.

- A set of natural numbers

- A set of rational numbers

 

We call the set that is not a countable set an uncountable set.

 

The set of real numbers is an uncountable set.

Cantor proved it by Cantor's diagonal argument.

 

 

We define the ratio of the circumference of a circle to its diameter, pi by the following series.

(Leibniz series)

The above π is a constant whose infinite digits have been determined.

 

We define pi by the following infinite decimal number.

(Pi)

The above π is a constant whose infinite digits have been determined.

 

We define real numbers as infinite digits decimal numbers.

 

We show an example of a real number.

(An example of a real number)

The above real number a is a constant.

 

We think the following sequence {a_n} that each digit is gradually determined.

 

The limit of this sequence {a_n} is the real number one.

We abbreviate the above formula as follows.

The real number one is a constant.

 

In this section, we prove that the set of real numbers is not a countable set in the Cantor's diagonal argument. Georg Cantor first used the diagonal argument in 1891.

 

The diagonal argument is a proof by contradiction.

We assume the following proposition as assumption of the proof by contradiction.

- A set of real numbers is a countable set.

 

We express the region that is greater than or equal to zero and less than one as the symbol (0, 1).

 

 

I 1 less than the real number of the section and (0, 1).

 

The region (0, 1) is a part of the set of real numbers. Therefore, if the region is not a countable set, the set of real numbers is not a countable set. Then we target the region (0, 1) in order to proceed with the proof.

 

By assumption, we can number all the elements in the region (0, 1).

 

We express these real numbers by the following decimal numbers.

 

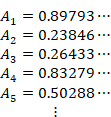
Specifically, we show it as follows.

 

We can express the same value by the different forms for decimal numbers as follows.

We adopt the rule that we always express the form 0.0999… of the right-hand side in the above case.

 

Here, we make the following new real number.

 

We determine the digit b_n by the following rule.

(Rule)

 

The digits a_11, a_22,…are arranged in a diagonal line as follows.

Specifically, we show it as follows.

 

In the above example, the real number B becomes the following decimal number.

 

There is the real number B in the region (0, 1).

However, there is not the real number B in the above table, because the following proposition holds.

 

(Proposition)

 

The real B does not have the digit 9 that continues like a number 0.999… because any digit of the real B is one or two.

 

It is contrary to the assumption that the real B does not exist in the above table.

This is contradiction. Therefore, the assumption is incorrect because of the proof by contradiction. This proof assumed the following.

 

- A set of real numbers is a countable set.

 

The above assumption is incorrect. Therefore, the set of real numbers is not a countable set.

(Q.E.D.)

 

Potential infinite mathematics is mathematics that considers the potential infinity.

 

We define the finite set of natural numbers as follows.

(The finite set of natural numbers)

We call the number of elements of a finite set the order.

 

We show the order of a finite set of natural numbers as follows.

 

We define the finite set of rational numbers as follows.

(The finite set of rational numbers)

 

We show the order of a finite set of rational numbers as follows.

 

We call the numbered finite subset of rational numbers a finite sequence.

 (The Finite sequence)

 

In potential infinite mathematics, we define the Cauchy finite sequence as follows.

(Cauchy finite sequence)

 

The natural number is not uniquely determined for the error ε. However, we can choose a certain appropriate natural number m for the above condition. This natural number m depends on the error ε. Then, we interpret this natural number as a function of the error ε.

 

Therefore, we interpret the elements a_m of the sequence as a function of the error ε.

 

We call the above function as a potential infinite real number.

We define potential infinite real numbers as follows.

(Potential infinite real numbers)

 

We call potential infinite real numbers real numbers.

We abbreviate it as follows.

(The real number)

 

We define the finite set of real numbers as follows.

(The finite set of real numbers)

 

We show the order of a finite set of real numbers as follows.

 

We consider the following special Cauchy finite sequence.

(The special Cauchy finite sequence)

 

We define the potential infinitesimal by the above special Cauchy finite sequence.

 

(The potential infinitesimal)

 

We call the potential infinitesimal the zero.

We abbreviate it as follows.

(Zero)

 

We consider the following special Cauchy finite sequence.

(The special Cauchy finite sequence)

 

We define the potential infinity by the above special Cauchy finite sequence.

 

(The potential infinity)

 

We call the potential infinity the infinity.

We abbreviate it as follows.

(Infinity)

 

We define the potential infinite limit by the potential infinitesimal and the potential infinity.

(The potential infinite limit)

 

We call the potential infinite limit the limit.

We abbreviate it as follows.

(Limit)

 

We define the potential infinite set of natural numbers as follows.

(The potential infinite set of natural numbers)

 

We call the potential infinite set of natural numbers as the set of natural numbers.

We abbreviate it as follows.

(The set of natural numbers)

 

We abbreviate the set of natural numbers as follows.

(The set of natural numbers)

 

We define the potential infinite set of rational numbers as follows.

(The potential infinite set of rational numbers)

 

We call the potential infinite set of rational numbers as the set of rational numbers.

We abbreviate it as follows.

(The set of rational numbers)

 

We abbreviate the set of rational numbers as follows.

(The set of rational numbers)

 

We define the potential infinite sequence as follows.

(The potential infinite sequence)

 

We call the potential infinite sequence as the sequence.

(The Sequence)

 

We abbreviate the sequence as follows.

(The sequence)

 

We define the potential infinite set of real numbers as follows.

(The potential infinite set of real numbers)

 

We call the potential infinite set of real numbers as the set of real numbers.

We abbreviate it as follows.

(The set of real numbers)

 

We abbreviate the set of real numbers as follows.

(The set of real numbers)

 

The potential countable set is the following set.

 

- The set we can number with the potential infinite set of natural numbers to all elements.

 

We show examples of the potential countable sets as follows.

- A set of natural numbers

- A set of rational numbers

- A set of real numbers

 

In potential infinite mathematics, we call a potential countable set as the countable set.

 

 

We consider the following sequence {π_n}.

 

(Leibniz sequence)

This sequence satisfies the following definition of Cauchy finite sequence.

(Cauchy finite sequence)

 

We define the potential infinite pi by the Cauchy finite sequence.

(The potential infinite pi)

 

We call the potential infinite pi pi.

We abbreviate it as follows.

(Pi)

 

The above pi is a function of the error ε.

Finite digits have been determined.

 

We think the following sequence {π_n} that each digit is gradually determined.

 

We call the element π_n of the above sequence the finite pi.

 

We show the potential infinite pi as follows.

(The potential infinite pi)

We abbreviate the above equation as follows.

The potential infinite pi π (ε) is not a constant.

It is a function depending on an error ε.

Finite digits of the potential infinite pi have been determined.

 

We abbreviate the potential infinite pi as follows.

 

Therefore, we have the following equation.

 

In addition, we call the following real number the actual infinite pi.

(The actual infinite pi)

The above value is not a variable quantity.

It is a constant quantity not depending on the error ε.

 

The actual infinite digits of the actual infinite pi have been determined.

 

 

We express the finite decimal number as the decimal number of finite digit binary as follows.

(The finite decimal number)

The natural number n is even and we define m as follows.

We express negative numbers as the two's complement.

 

We define the potential infinite decimal number as follows.

(The potential infinite decimal number)

The potential infinite decimal number a (ε) is a function depending on the error ε.

 

We call finite decimal numbers finite real numbers.

We call potential infinite decimal numbers potential infinite real numbers.

We abbreviate a potential infinite real number as follows.

(A potential infinite real number)

 

We call potential infinite real numbers real numbers.

We abbreviate it as follows.

(The real number)

 

We define actual infinite real numbers as follows.

(Actual infinite real numbers)

An actual infinite real number a_∞ is a constant not depending on the error ε.

 

 

We think the following sequence that each digit is gradually determined.

 

We define a potential infinite real number a (ε) by a potential infinite limit of this sequence.

 

A potential infinite real number a (ε) is not a constant.

It is a function depending on the error ε.

 

We abbreviate this formula as follows.

 

We abbreviate the above equation as follows.

 

We abbreviate the above equation as follows.

Therefore, in potential infinite mathematics, a potential infinite real number one is not a constant. It is a function depending on the error ε.

 

In order to indicate that a potential infinite real number one is a function depending on the error ε explicitly, we express it as follows.

(An infinite real number)

 

We express the potential infinite real number n as follows.

(The potential infinite real number)

 

We define the finite set of finite real numbers as follows.

 

(The finite set of finite real number)

We call the finite set of finite real numbers the finite set of real numbers shortly.

 

We define the potential infinite set of the potential infinite real numbers by the following formula.

(The potential infinite set of the potential infinite real numbers)

 

We call the potential infinite set of the potential infinite real numbers the set of real numbers shortly.

We abbreviate the set of real numbers as follows.

 

The potential infinite set of finite real numbers does not exist, but a finite set of potential infinite real numbers exists.

 

For example, the set  of finite real numbers is not potential infinite set, because the order of the set  of finite real numbers is 2ⁿ.

 

On the other hand, we show an example of a finite set of the potential infinite real number as follows.

(The finite set of the potential infinite real number)

 

 

In this section, we prove that the set of real numbers is a countable set by the Cantor's diagonal argument.

 

The diagonal argument is a proof by contradiction.

We assume the following proposition as assumption of the proof by contradiction.

- We can number the finite set of real numbers.

 

We express a finite set of real numbers as follows.

 

The natural number n is even, and we define M as follows.

 

We express the finite real number as the decimal numbers of binary as follows.

 

Specifically, we show it as follows.

 

In the finite real numbers, we cannot express the same value of the decimal number by the different forms. We show an example as follows.

 

Here, we make the following new finite real number.

 

We determine the digit b_n by the following rule.

(Rule)

 

The digits a_11, a_22,…are arranged in a diagonal line as follows.

 

Specifically, we show it as follows.

 

In the above example, the real number B becomes the following decimal number.

 

 

There is the real number B in the set {A₁, A₂, A₃,…, A_n}, because the following proposition holds.

 

(Proposition)

 

Indeed, the finite real B is not in the set {A₁, A₂, A₃,… , A_n}. Since this is a contradiction, it seems that the following assumption is incorrect.

 

- We can number the finite set of real numbers.

 

However, the finite real number B is in the set {A_n+1,…, A_M}. Here, M is 2ⁿ. Therefore, it is not actually a contradiction.

 

We cannot number the finite set  of real numbers by the set   of natural numbers. However, we can number the finite set  of real numbers by the set  of natural numbers.

 

 

 

In potential infinite mathematics, a correct proposition for a finite set is a correct proposition for a potential infinite set, because the order of a potential infinite set is the order of a finite set depending on the error ε. Therefore, the following proposition is satisfied.

 

- We can number the set of real numbers.

 

Thus, the set of real numbers is a countable set.

(Q.E.D.)

 

The figure of a finite set of real numbers is not a square. It is a rectangle. The order of the set of n-digit real numbers is 2ⁿ. This is a vertical rectangle.

 

If the figure of a finite set of real numbers is a square, we can draw a diagonal line having an angle of 45 degrees. However, if the figure of a finite set of real numbers is a rectangle, we cannot draw a diagonal line having an angle of 45 degrees.

This fact does not change even in the potential infinite limit.

 

I think that it is a problem to draw a diagonal line having an angle of 45 degrees on the rectangle in the Cantor's diagonal argument.

 

 

In this article, we consider the Cantor's diagonal argument in actual infinite mathematics and potential infinite mathematics. We show the conclusion as follows.

 

- The set of real numbers is not a countable set in actual infinite mathematics.

- The set of real numbers is countable set in potential infinite mathematics.

 

Dedekind defined the real number in the Dedekind cut in 1872. [1]

 

We divide the set  of rational numbers to a set A and a set B of rational numbers.

 

We suppose that we have the following inequality for any element a of the set A and any element b of the set B,

 

We call the cut (A, B) a Dedekind cut.

 

We define the real number x by Dedekind cut (A, B) as follows.

(Dedekind cut)

 

The real number of actual infinite mathematics is a fixed cut (A, B).

The real number of potential infinite mathematics is a pair of variables (a, b).

 

Cantor defined a real number by the Cauchy sequence in 1872.

(The real number)

 

The real number of actual infinite mathematics is a constant not depending on the error ε.

The real number of potential infinite mathematics is a variable a_n depending on the error ε.

 

Peano proposed the following axioms in 1891.

 

(1) 1 is a natural number.

(2) If a is a natural number, a+1 is a natural number.

(3) If a+1=1, a is not a natural number.

(4) If a+1=b+1, a=b.

(5) If a set A satisfies the following two conditions, then any natural number is in the set A,

[1] 1 is in A.

[2] If a is in A, a+1 is in A.

 

In actual infinite mathematics, the above set A is fixed. It contains all natural numbers from the beginning.

 

In potential infinite mathematics, the order of the above set A is a variable |A|.

 

 

Russell introduced the axiom of infinity in 1904.

 

The axiom of infinity ensures the presence of the following infinite set A.

(Axiom of infinity)

We can express it succinctly as follows.

 

In actual infinite mathematics, an infinite set A is fixed. It contains all elements from the beginning. We call this axiom of infinity of actual infinite mathematics the axiom of actual infinity.

 

In potential infinite mathematics, the order of an infinite set A is a variable |A|. We call the axiom of infinity of potential infinite mathematics the axiom of potential infinity.

 

In Cantor's diagonal argument, we express real numbers as the following decimal numbers.

 

We interpret the real number A_n as a set A_n.

 

We define a family as follows.

 

The set A_n is in the above family.

 

When we give the number n of the set A_n,

 

We define a function f (A_n) having the following rules of choice.

(The rules of choice)

 

We call this function the choice function.

(Choice function)

 

It is not a complete description, but we call the following proposition the axiom of choice.

(The axiom of choice)

 

We can express it succinctly as follows.

 

Zermelo published axiom of choice in 1904.

 

Speaking inaccurate, the axiom of choice is an axiom that guarantees the existence of a choice function for any set.

 

In actual infinite mathematics, all rules of choice have been completed from the beginning. We call the axiom of choice of actual infinite mathematics the axiom of actual infinite choice.

 

In potential infinite mathematics, the number of rules of choice depends on the number of the groups A_n. We call the axiom of choice of potential infinite mathematics the axiom of potential infinite choice.

 

 

In potential infinite mathematics, we defined the potential infinite real number a (ε) as follows.

(The potential infinite real number)

 

Therefore, the potential infinite real number a (ε) has the uncertainty of error ε. This is similar to the uncertainty of the position and momentum in quantum mechanics. Then, we construct a new mathematics, quantum number theory by extending potential infinite mathematics.

 

We show the natural number as follows.

(The natural number)

 

We define the natural generating function by complex number z.

(The natural generating function)

 

We abbreviate the natural generating function as follows.

(The natural generating function)

 

We obtain the natural derived function by differentiating the natural generating function s-times.

(The natural derived function)

 

We abbreviate the natural derived function as follows.

(The natural derived function)

 

We define the mean natural derived function by averaging it in contour integral.

(The mean natural derived function)

 

We interpret the above averaging as quantization. Then, we call the mean natural derived function the quantum natural derived function.

 

We call the quantum natural derived function the quantum natural function shortly.

We abbreviate it as follows.

(The quantum natural function)

 

We define quantum natural number as follows.

(The quantum natural number)

 

The quantum natural number has the uncertainty of the error ε.

 

We define the potential infinite sum of the quantum natural numbers as follows.

 

Then, the potential infinite sum of quantum natural numbers becomes -1/12.

 

We abbreviated the above equation as follows.

 

Therefore, we interpret that the above strange result in the zeta function is a special phenomenon of quantum mathematics.

 

In writing this article, I thank from my heart to TY and NS who gave valuable advice to me.