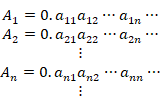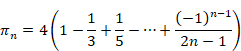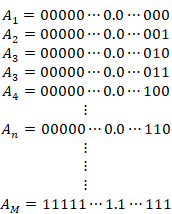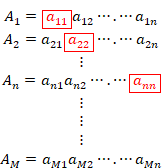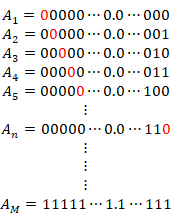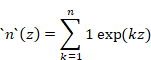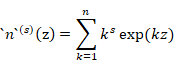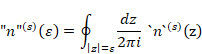実無限と可能無限によるカントールの対角線論法の考察
2020/3/27
公開日 2015/6/26
Koji Sugiyama
対角線論法とは、実数の集合が数えることのできない集合であることを証明する方法です。
本記事では、実無限と可能無限でカントールの対角線論法を考察します。
実無限は変化しない無限です。それは最初から完成しています。一方、可能無限は変化する無限です。それは決して完成しません。現代数学にとって、実無限は公理です。そのため「実無限は存在しない」という主張は同意を得られません。そこで、本記事は数学を実無限数学と可能無限数学に分離します。
n個の自然数の集合を有限集合 
と表現します。そして、 n 桁の小数の有限集合を 
とします。小数は二進法で表現します。その集合の要素の個数は2nです。したがって、0以上1未満の小数の有限集合を次の表で表現できます。
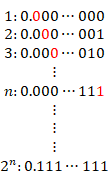
その表の行数は2nです。
この表に対角線論法を適用すると、自然数の有限集合と小数の有限集合は一対一対応しません。なぜなら、小数の有限集合
の要素数 2n
は、自然数の有限集合の要素数 n より多いからです。しかし、n桁の小数の有限集合 は、M = 2n個の自然数を持つ有限集合 
と一対一対応します。
この小数の桁数を可能無限桁にして実数を構成します。この実数の集合は可算集合となります。しかし、現代の数学では、可能無限桁の小数は実数ではありません。なぜならば実数は最初から実無限桁を持つからです。そこで、数学を実無限数学と可能無限数学に分離します。そして可能無限数学の実数を可能無限桁の小数と定義します。
本記事では、実無限数学の実数の集合が可算集合でないことを証明し、可能無限数学の実数の集合が可算集合であることを証明します。
目次
実無限と可能無限でカントールの対角線論法を考察します。
実無限は変化しない無限です。それは最初から完成しています。一方、可能無限は変化する無限です。それは決して完成しません。本記事では、実無限数学の実数の集合が可算集合でないことを証明し、可能無限数学の実数の集合が可算集合であることを証明します。
歴史上、次のような数学者が、実無限を支持しました。
・デデキント (1831-1916)
・カントール (1845-1918)
・ヒルベルト (1852-1943)
・ラッセル (1872-1970)
・ゲーデル (1906-1978)
カントールは1886年にエネストレームへの手紙で次のように述べています。
可能無限と実無限の概念は大きく異なるものです。可能無限は変化する有限量です。それはすべての有限量の極限を越えて増大します。一方、実無限はそれ自身固定的な定数です。それはすべての有限量を超えて位置する量です。その違いにも関わらず、両者とも変化すると考え混乱される方がいることは残念です。
一方、次のような数学者が実無限に反対しました。
・ガウス (1777-1855)
・コーシー (1789-1857)
・クロネッカー (1823-1891)
・ポアンカレ (1854-1912)
・ワイル (1885-1955)
ガウスは1831年にシューマッハへの手紙で次のように述べています。
私は、無限大を完成したものとして取り扱うことに反対します。数学において無限は決して許されません。無限は単に話す方法にすぎません。その真の意味は、ある量が際限なく増大することが許されている時に、それに合わせて、ある比率がある極限に、無制限に近づくことです。
また、ポアンカレは1913年に出版された著作で次のように述べています。
実無限は存在しません。カントールの支持者達は、そのことを忘れ矛盾に陥ってしまったのです。確かにカントール主義は便利な手法を提供しました。しかし、それは、明確に用語が定義された現実の問題に適用される場合に限ります。その場合においてのみ、我々は安全に問題を解くことができるのです。
しかし、現代数学では、実無限は公理です。したがって、現在の数学で実無限を否定することはできません。そこで、実無限を否定するのではなく、実無限を前提とする数学と、可能無限を前提とする数学に分離します。そのため、本記事では、現在の数学を次の二つに分離することを提案します。
・実無限数学
・可能無限数学
実無限数学は、実無限を考察の対象とする数学です。
自然数の集合を次のように定義します。
(自然数の集合)
|
|
(2.1) |
上記の集合を次のように略記します。
|
|
(2.2) |
自然数の集合は、すべての自然数を含んでいます。
有理数の集合を次のように定義します。
(有理数の集合)
|
|
(2.3) |
|
|
(2.4) |
有理数の集合は、すべての有理数を含んでいます。
番号付けされた、有理数の部分集合を数列と呼びます。
(数列)
|
|
(2.5) |
上記の数列を次のように略記します。
|
|
(2.6) |
コーシーは1821年に次のコーシー列を定義しました。
(コーシー列)
|
{an}を有理数の数列とする。 任意の正の有理数ε に対し、ある適当な自然数Nが存在し、
を満たすすべての自然数nとmに対し、不等式
が成り立つ。 |
文字εはイプシロンと読みます。それはコーシー列の誤差を意味します。
コーシー列{an}は、十分大きいnで、誤差εの範囲で値がほとんど変化しない数列です。
カントールは1872年にコーシー列anで実数aを定義しました。
(実数)
|
コーシー列{an}において 任意の正の有理数εに対し、ある適当な自然数Nが存在し、
を満たすすべての自然数nに対し、
が成り立つ。 |
実数aは誤差εに依存しない定数です。
カントールは実数を連続体と呼びました。
極限を次のように定義します。
(極限)
|
コーシー列{an}において 任意の正の有理数ε に対し、ある適当な自然数Nが存在し、
を満たすすべての自然数nに対し、
が成り立つ。 |
上記の極限は、次のように簡潔に表現できます。
(極限)
|
|
(2.7) |
上記の式を次のように略記します。
(極限)
|
|
(2.8) |
実数の集合
を実数aで次のように定義します。
(実数の集合)
|
|
(2.9) |
実数の集合は、すべての実数を含んでいます。
カントールは、集合の要素数を一般化した概念として濃度(基数)を導入しました。
自然数の集合の濃度は次の通りです。
|
|
(2.10) |
記号 
はアレフ・ゼロと読みます。記号 
はヘブライ文字の最初の文字です。
実数の集合の濃度は次の通りです。
|
|
(2.11) |
可算集合は次のような集合です。
・すべての要素に自然数で番号付けできる集合。
可算集合は、ゲオルグ・カントールが1891年に提唱しました。
可算集合の例は次の通りです。
・自然数の集合
・有理数の集合
可算集合でない集合を非可算集合と呼びます。
実数の集合は、非可算集合です。
それは、カントールが対角線論法で証明しました。
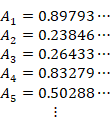
円周率は次の級数で定義します。
(ライプニッツの級数)
|
|
(2.12) |
上記のπは定数であり、無限の桁が確定しています。
無限小数で円周率を定義します。
(円周率)
|
|
(2.13) |
上記のπは定数であり、無限の桁が確定しています。
実数を無限桁の十進法の小数で定義します。
実数の例を次に示します。
(実数の例)
|
|
(2.14) |
上記の実数aは定数です。
次のように一桁ずつ各桁が決まっていく数列{an}を考えます。
|
|
(2.15) |
|
|
(2.16) |
|
|
(2.17) |
|
|
(2.18) |
この数列{an}の極限は実数1になります。
|
|
(2.19) |
上記の式を次のように略記します。
|
|
(2.20) |
実数1は定数です。
本節では、実数の集合が可算集合でないことをカントールの対角線論法で証明します。対角線論法はゲオルグ・カントールが1891年に初めて用いました。
対角線論法は背理法です。背理法の仮定として次の命題を仮定します。
・実数の集合は可算集合である。
0以上1未満の実数の区間を記号(0,1)で表現します。
区間(0,1)は実数の集合の一部です。そのため、(0,1)が可算集合でないならば実数の集合も可算集合ではありません。そこで、区間(0,1)を対象として証明を進めます。
仮定より、区間(0,1)にあるすべての要素を番号付けできます。
|
|
(2.21) |
これらの実数を十進法の小数で次のように表現します。
|
|
(2.22) |
具体的には、次の通りです。
|
|
(2.23) |
十進法の小数は、次のように同じ値を異なる形式で表現できます。
|
|
(2.24) |
上記のようなケースでは、常に右辺の形式0.0999…で表現する規則を採用します。
ここで次の新しい実数を作ります。
|
|
(2.25) |
桁bnは次の規則で決定します。
(規則)
|
実数Bの桁b1は、実数A1の桁a11が偶数ならば1、奇数ならば2とする。 実数Bの桁b2は、実数A2の桁a22が偶数ならば1、奇数ならば2とする。 実数Bの桁b3は、実数A3の桁a33が偶数ならば1、奇数ならば2とする。 … 実数Bの桁bnは、実数Anの桁ann が偶数ならば1、奇数ならば2とする。 … |
桁a11, a22,…は次のように対角線上に並びます。
|
|
(2.26) |
具体的には、次の通りです。
|
|
(2.27) |
上記の例では、実数Bは次のような小数となります。
|
|
(2.28) |
実数Bは区間(0,1)に存在します。
しかし、実数Bは上記の表に存在しません。なぜならば、次の命題が成り立つからです。
(命題)
|
実数Bの桁b1は実数A1の桁a11と異なる。 実数Bの桁b2は実数A2の桁a22と異なる。 実数Bの桁b3は実数A3の桁a33と異なる。 … 実数Bの桁bnは実数Anの桁annと異なる。 … |
実数Bの桁9が、数字0.999…のように続くことはありません。なぜならば、実数 B の任意の桁は1または2だからです。実数Bが上記の表に存在しないことは、仮定に反します。これは矛盾です。したがって、背理法により、仮定は誤りです。この証明は、次のことを仮定していました。
・実数の集合は可算集合である。
上記の仮定は誤りです。ゆえに実数の集合は可算集合ではありません。
(証明終了)
可能無限数学は、可能無限を考察の対象とする数学です。
自然数の有限集合を次のように定義します。
(自然数の有限集合)
|
|
(3.1) |
有限集合の要素の個数を位数と呼びます。
自然数の有限集合の位数は次の通りです。
|
|
(3.2) |
有理数の有限集合を次のように定義します。
(有理数の有限集合)
|
|
(3.3) |
|
|
(3.4) |
有理数の有限集合の位数は次の通りです。
|
|
(3.5) |
有理数の有限集合の一部の要素に自然数の有限集合で番号付けしたものを有限数列と呼びます。
(有限数列)
|
|
(3.6) |
可能無限数学ではコーシー有限数列を次のように定義します。
(コーシー有限数列)
|
有限数列{a1,a2,a3,…,aＭ}において、M = 2Nとする。 任意の正の有理数εに対し、ある適当な自然数Nが存在し、
を満たすすべての自然数 n, mに対し、
が成り立つ。 |
誤差εに対し、自然数mは一意に決まりません。しかし、上記の条件を満たすある適当な自然数mを選ぶことができます。この自然数mは誤差ε に依存します。そこで、この自然数mを誤差εの関数と解釈します。
|
|
(3.7) |
したがって、数列の要素amは誤差εの関数と解釈できます。
|
|
(3.8) |
上記の関数を可能無限実数と呼ぶことにします。可能無限実数を次のように定義します。
(可能無限実数)
|
コーシー有限数列{a1,a2,a3,…,aＭ}においてM = 2Nとする。 任意の正の有理数εに対し、ある適当な自然数Nが存在し、
を満たすすべての自然数 nに対し、
が成り立つ。 |
可能無限実数を実数と呼び、次のように略記します。
(実数)
|
|
(3.9) |
実数の有限集合を次のように定義します。
(実数の有限集合)
|
|
(3.10) |
|
|
(3.11) |
実数の有限集合の位数は次の通りです。
|
|
(3.12) |
次の特別なコーシー有限数列を考えます。
(特別なコーシー有限数列)
|
有理数の有限数列{a1,a2,a3,...,aＭ}においてM=2Nとする。 任意の正の有理数εに対し、ある適当な自然数Nが存在し、
を満たすすべての自然数nに対し、
が成り立つ。 |
上記の特別なコーシー有限数列で可能無限小を定義します。
(可能無限小)
|
|
(3.13) |
可能無限小を零と呼び、次のように略記します。
(零)
|
|
(3.14) |
次の特別なコーシー有限数列を考えます。
(特別なコーシー有限数列)
|
有理数の有限数列{a1,a2,a3,...,aＭ}においてM=2Nとする。 任意の正の有理数εに対し、ある適当な自然数Nが存在し、
を満たすすべての自然数nに対し、
が成り立つ。 |
上記の特別なコーシー有限数列で可能無限大を定義します。
(可能無限大)
|
|
(3.15) |
可能無限大を無限大と呼び、次のように略記します。
(無限大)
|
|
(3.16) |
可能無限小と可能無限大を合わせて可能無限極限を定義します。
(可能無限極限)
|
|
(3.17) |
可能無限極限を極限と呼び、次のように略記します。
(極限)
|
|
(3.18) |
自然数の可能無限集合を次のように定義します。
(自然数の可能無限集合)
|
|
(3.19) |
自然数の可能無限集合を自然数の集合と呼び、次のように略記します。
(自然数の集合)
|
|
(3.20) |
自然数の集合を次のように略記します。
(自然数の集合)
|
|
(3.21) |
|
|
(3.22) |
有理数の可能無限集合を次のように定義します。
(有理数の可能無限集合)
|
|
(3.23) |
有理数の可能無限集合を有理数の集合と呼び、次のように略記します。
(有理数の集合)
|
|
(3.24) |
有理数の集合を次のように略記します。
(有理数の集合)
|
|
(3.25) |
|
|
(3.26) |
可能無限数列を次のように定義します。
(可能無限数列)
|
|
(3.27) |
可能無限数列を数列と呼び、次のように略記します。
(数列)
|
|
(3.28) |
数列を次のように略記します。
(数列)
|
|
(3.29) |
|
|
(3.30) |
実数の可能無限集合を次のように定義します。
(実数の可能無限集合)
|
|
(3.31) |
実数の可能無限集合を実数の集合と呼び、次のように略記します。
(実数の集合)
|
|
(3.32) |
実数の集合を次のように略記します。
(実数の集合)
|
|
(3.33) |
|
|
(3.34) |
可能可算集合とは次のような集合です。
・要素に自然数の可能無限集合で番号付けできる集合。
可能可算集合の例は次の通りです。
・自然数の無限集合
・有理数の無限集合
・実数の無限集合
可能無限数学では、可能可算集合を可算集合と呼びます。
次の数列{πn}を考えます。
(ライプニッツの数列)
|
|
(3.35) |
|
|
(3.36) |
|
|
(3.37) |
この数列は次のコーシー有限数列の定義を満たします。
(コーシー有限数列)
|
有理数の有限数列{π1, π2, π3,…, πＭ}においてM = 2Nとする。 任意の正の有理数ε に対し、ある適当な自然数Nが存在し、
を満たすすべての自然数n, mに対し、
が成り立つ。 |
コーシー有限数列で可能無限円周率を定義します。
(可能無限円周率)
|
|
(3.38) |
可能無限円周率を円周率と呼び、次のように略記します。
(円周率)
|
|
(3.39) |
上記の円周率は誤差εの関数であり、有限の桁が確定しています。
次のように一桁ずつ各桁が決まっていく数列を考えます。
|
|
(3.40) |
|
|
(3.41) |
|
|
(3.42) |
|
|
(3.43) |
|
|
(3.44) |
上記の数列の要素πnを有限円周率と呼ぶことにします。
可能無限円周率は次の通りです。
(可能無限円周率)
|
|
(3.45) |
上記の式を次のように略記します。
|
|
(3.46) |
可能無限円周率π(ε)は定数ではありません。それは誤差ε に依存する関数です。
可能無限円周率は、有限の桁が確定しています。
可能無限円周率を次のように略記します。
|
|
(3.47) |
ゆえに、次の式が成立します。
|
|
(3.48) |
また、次の実数を実無限円周率と呼ぶことにします。
(実無限円周率)
|
|
(3.49) |
上記の値は変化量ではありません。
それは、誤差ε に依存しない固定量です。
実無限円周率は、実無限個の桁が確定しています。
有限小数を有限桁の二進法の小数で次のように表現します。
(有限小数)
|
|
(3.50) |
|
|
(3.51) |
自然数nは偶数とし、mを次のように定めます。
|
|
(3.52) |
負の数は2の補数で表現します。
可能無限小数を次のように定義します。
(可能無限小数)
|
|
(3.53) |
可能無限小数a(ε)は誤差εに依存する関数です。
有限小数を有限実数と呼びます。
可能無限小数を可能無限実数と呼びます。
可能無限実数を次のように略記します。
(可能無限実数)
|
|
(3.54) |
可能無限実数を実数と呼びます。
実数を次のように略記します。
(実数)
|
|
(3.55) |
実無限実数を次のように定義します。
(実無限実数)
|
|
(3.56) |
実無限実数a∞ は誤差εに依存しない定数です。
次のように一桁ずつ各桁が決まっていく数列を考えます。
|
|
(3.57) |
|
|
(3.58) |
|
|
(3.59) |
|
|
(3.60) |
|
|
(3.61) |
この数列の可能無限極限で可能無限実数a(ε)を定義します。
|
|
(3.62) |
可能無限実数a(ε)は定数ではありません。誤差εに依存する関数です。
この式を次のように略記します。
|
|
(3.63) |
上記の式を次のように略記します。
|
|
(3.64) |
上記の式を次のように略記します。
|
|
(3.65) |
したがって、可能無限数学では、可能無限実数1は定数ではありません。誤差εに依存する関数です。
可能無限実数1が誤差ε に依存する関数であることを明示的に示す場合は、次のように表記することにします。
(可能無限実数)
|
|
(3.66) |
可能無限実数nは次のように表記します。
(可能無限実数)
|
|
(3.67) |
有限実数の有限集合を次のように定義します。
(有限実数の有限集合)
|
|
(3.68) |
|
|
(3.69) |
有限実数の有限集合を短く、実数の有限集合と呼ぶことにします。
可能無限実数の可能無限集合を次の式で定義します。
(可能無限実数の可能無限集合)
|
|
(3.70) |
可能無限実数の可能無限集合を短く、実数の集合と呼びます。
実数の集合を次のように略記します。
|
|
(3.71) |
有限実数の可能無限集合は存在しませんが、可能無限実数の有限集合は存在します。
例えば、有限実数の集合 の位数は2nであるため、有限実数の集合 は可能無限集合ではありません。
一方、可能無限実数の有限集合の例は次の通りです。
(可能無限実数の有限集合)
|
|
(3.72) |
本節は、実数の集合が可算集合であることをカントールの対角線論法で証明します。対角線論法は背理法であるため、背理法の仮定として次の命題を仮定します。
・実数の有限集合を番号付けできる。
実数の有限集合を次のように表現します。
|
|
(3.73) |
自然数nは偶数とし、Mを次のように定めます。
|
|
(3.74) |
この有限実数を二進法の小数で次のように表現します。
|
|
(3.75) |
具体的には、次の通りです。
|
|
(3.76) |
有限実数では、同じ数が異なる形式で表現されることはありません。例は次のとおりです。
|
|
(3.77) |
ここで次の新しい有限実数を作ります。
|
|
(3.78) |
数字bnは次の規則で決定します。
(規則)
|
有限実数Bの数字b1は、有限実数A1の数字a11が0ならば1、1ならば0とする。 有限実数Bの数字b2は、有限実数A2の数字a22が0ならば1、1ならば0とする。 有限実数Bの数字b3は、有限実数A3の数字a33が0ならば1、1ならば0とする。 … 有限実数Bの数字bnは、有限実数Anの数字annが0ならば1、1ならば0とする。 |
数字a11, a22,…は次のように対角線上に並びます。
|
|
(3.79) |
具体的には、次の通りです。
|
|
(3.80) |
上記の例では、有限実数Bは次のような数字になります。
|
|
(3.81) |
有限実数Bは集合 {A1, A2, A3,…, An} には存在しません。
なぜならば、次の命題が成り立つからです。
(命題)
|
有限実数Bの数字b1は、有限実数A1の数字a11と異なる。 有限実数Bの数字b2は、有限実数A2の数字a22と異なる。 有限実数Bの数字b3は、有限実数A3の数字a33と異なる。 … 有限実数Bの数字bnは、有限実数Anの数字annと異なる。 |
確かに、有限実数Bは集合 {A1, A2, A3,… , An} に存在しません。これは矛盾であるため、次の仮定は正しくないように思えます。
・実数の有限集合を番号付けできる。
しかし、有限実数Bは集合{An+1,…, AM}に存在します。ここでMは2nです。したがって、実際には矛盾はありません。
有限実数の集合 は自然数の有限集合 で番号付けることはできません。しかし、自然数の有限集合で番号付けることができます。
可能無限数学では、有限集合で正しい命題は可能無限集合で正しい命題です。なぜならば、可能無限集合の位数は誤差εに依存する有限集合の位数だからです。したがって、次の命題が成立します。
- 実数の集合は番号付けできる。
したがって、実数の集合は可算集合です。
(証明終了)
実数の有限集合の絵は正方形ではありません。それは長方形です。n桁の実数の有限集合の位数は2n個です。これは、縦長の長方形です。
もし、実数の有限集合の絵が正方形ならば、45度の角度を持つ対角線を引くことができます。しかし、実数の有限集合の絵が長方形ならば、45度の角度を持つ対角線を引くことはできません。この事実は、可能無限極限でも変わりません。
カントールの対角線論法において、長方形に45度の対角線を引くことは問題であると考えます。
本記事では、実無限数学と可能無限数学でカントールの対角線論法を考察しました。結論は次の通りです。
・実無限数学では、実数の集合は可算集合でない。
・可能無限数学では、実数の集合は可算集合である。
デデキントは1872年に、デデキント切断で実数を定義しました。 [1]
有理数の集合 
を有理数の集合Aと有理数の集合Bに分けます。
|
|
(6.1) |
集合Aの任意の要素aと、集合Bの任意の要素bに対して、次の不等式が成り立つとします。
|
|
(6.2) |
この切断(A,B)をデデキント切断と呼びます。
実数xをデデキント切断(A,B)で次のように定義します。
(デデキント切断)
|
集合Aの任意の要素aに対し、ある適当な要素xが存在し、 集合Bの任意の要素bに対して、
が成り立つ。 |
実無限数学の実数は固定的な集合の組(A, B)です。
可能無限数学の実数は変数の組(a, b)です。
カントールは1872年にコーシー列anで実数を定義しました。
(実数)
|
コーシー列{an}において 任意の正の有理数εに対し、ある適当な自然数Nが存在し、
を満たすすべての自然数nに対し、
が成り立つ。 |
実無限数学の実数は誤差εに依存しない定数aです。
可能無限数学の実数は誤差ε に依存する変数anです。
ペアノは1891年に次の公理を提案しました。
(1) 1は自然数である。
(2) aが自然数ならば、a+1は自然数である。
(3) a+1=1ならば、aは自然数ではない。
(4) a+1=b+1ならば、a=bである。
(5) 集合Aが次の二条件を満たすならば、任意の自然数は集合Aに含まれる。
[1] 1はAに含まれる。
[2] aがAに含まれるならば、a+1はAに含まれる。
実無限数学では、上記の集合Aは固定的です。それは、すべての自然数を最初から含んでいます。
可能無限数学では、上記の集合Aの位数は変数|A|です。
ラッセルは1904年に無限公理を導入しました。
無限公理では次の無限集合Aの存在を保証します。
(無限公理)
|
次の条件を満たす集合Aが存在する。 - 集合Aは、空集合を要素とする。
- 集合Aの任意の要素aに対し、和集合
が集合Aの要素として存在する。
|
簡潔に次のように表現できます。
|
|
(6.3) |
実無限数学では、無限集合Aは固定的です。それは、すべての要素を最初から含んでいます。実無限数学の無限公理を実無限公理と呼ぶことにします。
可能無限数学では、無限集合Aの位数は変数 |A| です。可能無限数学の無限公理を可能無限公理と呼ぶことにします。
6.5. ツェルメロの選択公理
カントールの対角線論法では、実数を次のような十進数で表現しました。
|
|
(6.4) |
この実数Anを集合Anと解釈します。
|
|
(6.5) |
族を次のように定義します。
|
|
(6.6) |
集合Anは上記の族の要素です。
|
|
(6.7) |
次の選択規則を持つ関数f (An)を定義します。
(選択規則)
|
関数f (A1)は、集合A1から数字a11を選択する。 関数f (A2)は、集合A2から数字a22を選択する。 関数f (A3)は、集合A3から数字a33を選択する。 … 関数f (An)は、集合Anから数字annを選択する。 … |
この関数を選択関数と呼びます。
(選択関数)
|
|
(6.8) |
完全な記述ではありませんが、次の命題を選択公理と呼びます。
(選択公理)
|
任意の集合Anに対し、ある適当な選択関数 f が存在し、
で得られる任意の要素ann に対し、
が成り立つ。 |
簡潔に次のように表現できます。
|
|
(6.9) |
選択公理はツェルメロが1904年に発表しました。
不正確に言えば、選択公理とは、任意の集合に対し選択関数の存在を保証する公理です。
実無限数学では、すべての選択規則が最初から完成しています。実無限数学の選択公理を実無限選択公理と呼ぶことにします。
可能無限数学では、選択規則の個数は、集合Anの個数に依存します。可能無限数学の選択公理を可能無限選択公理と呼ぶことにします。
可能無限数学では、可能無限実数a(ε)を次のように定義しました。
(可能無限実数)
|
コーシー列{a1,a2,a3,…,aＭ}においてM = 2Nとする。 任意の正の有理数εに対し、ある適当な自然数Nが存在し、
を満たすすべての自然数 nに対し、
が成り立つ。 |
したがって、可能無限実数a(ε)は誤差εの不確定性を持ちます。これは、量子力学における位置と運動量の不確定性に似ています。そこで、可能無限数学を拡張した新しい数学、量子数論を構築します。
自然数は次の通りです。
(自然数)
|
|
(7.1) |
複素数zで自然母関数を定義します。
(自然母関数)
|
|
(7.2) |
自然母関数を次のように略記します。
(自然母関数)
|
|
(7.3) |
自然母関数をs回微分し、自然導関数を得ます。
(自然導関数)
|
|
(7.4) |
自然導関数を次のように略記します。
(自然導関数)
|
|
(7.5) |
周回積分で平均化し平均自然導関数を定義します。
(平均自然導関数)
|
|
(7.6) |
上記の平均化は量子化と解釈できます。そこで、平均自然導関数を量子自然導関数と呼びます。
量子自然導関数を、短く量子自然関数と呼び、次のように略記します。
(量子自然関数)
|
|
(7.7) |
量子自然数を次のように定義します。
(量子自然数)
|
|
(7.8) |
量子自然数は誤差ε の不確定性を持ちます。
量子自然数の可能無限和を次のように定義します。
|
|
(7.9) |
すると、量子自然数の可能無限和は-1/12になります。
|
|
(7.10) |
上記の式を次のように略記します。
|
|
(7.11) |
したがって、ゼータ関数における上記の不思議な結果は量子数学の特別な現象だったと解釈できます。
本記事を作成するにあたり、貴重な助言を頂いた、NSさんとTYさんに心より感謝いたします。
9. 引用文献
|
[1] |
Dedekind, Richard, Stetigkeit und irrationale Zahlen (Continuity and irrational numbers), vol. 11, 1912, p. 24. |
