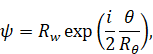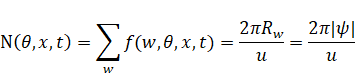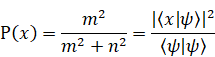Quantum probability from a geometrical interpretation of a wave function
Home > Quantum mechanics > Event theory
2019/02/17
Published 1999/11/21[1]
K. Sugiyama[2]
The probabilistic prediction of quantum theory is mystery. I solved the mystery by a geometrical interpretation of a wave function.
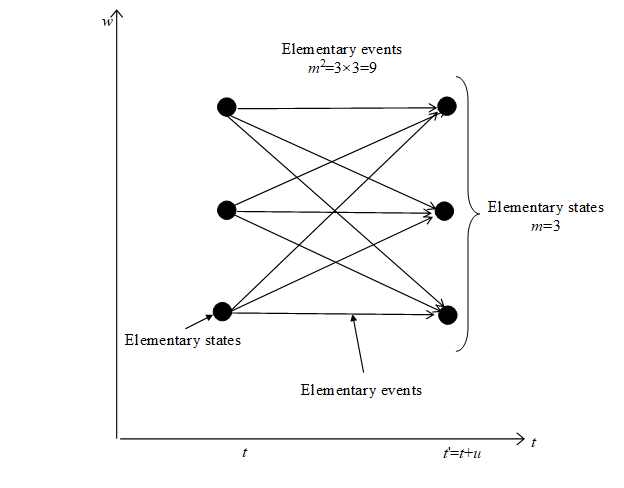
Figure 4-1: The number of elementary events is the square of the number of elementary states.
This suggests the unification between quantum theory and the theory of relativity. This suggests Many-Worlds Interpretation is true, too.
CONTENTS
2.1 An assumption of "no boundary"
2.2 An assumption of "a minimum unit"
2.3 An assumption of "a wave space"
2.4 An assumption of "a phase space"
2.5 An assumption of "an elementary state"
2.6 An assumption of "an elementary event"
1 Introduction
There was no theory for Many-Worlds Interpretation, which can provide the probabilistic prediction of quantum theory[3]. To obtain the probabilistic prediction of quantum theory, I suppose some assumptions and construct a theory for Many-Worlds Interpretation. I call the theory Many-Events Theory.
2 Assumptions
2.1 An assumption of "no boundary"
There are some physical quantities, position x, time t or phase θ, etc. I call these physical quantities "Position quantity." I suppose that all position quantities have no boundaries and are compact.
2.2 An assumption of "a minimum unit"
I suppose that all position quantities have a common minimum unit u.
2.3 An assumption of "a wave space"
I suppose new another position quantity w. I call a space of the quantity a wave space. This quantity has something to do with a wave function.
2.4 An assumption of "a phase space"
I suppose a phase space θ have a structure like a Mobius strip. This is analogous with a spin of an electron. Thus, I define a wave function
|
|
(2.1) |
where Rw is the radius of curvature of a wave space and Rθ is the radius of curvature of a phase space. Rw, Rθ and θ are functions of θ, x and t.
2.5 An assumption of "an elementary state"
I suppose that there is a minimum unit of a state. I call this an elementary state. For example in the quantum theory one particle’s elementary state is
|
|
(2.2) |
We can point the elementary state using a combination of position quantities. I suppose that same elementary state is only one. Thus, we can interpret it as a point in a space. A state is connected to a set of points.
2.6 An assumption of "an elementary event"
I call the transition from one elementary state to another elementary state an elementary event. I suppose that same elementary event is only one. Thus, we can interpret an elementary event as one line in a space. An event is connected to a set of lines.
All possible elementary events exist. This is analogous with path integrals.
3 The construction of a torus
To make the problem easy I think one particle. And, I use w, θ, x and t. I construct a torus,
|
|
(3.1) |
And, I define a point f on the torus,
|
|
(3.2) |
Rw is linear like a wave function approximately. If there is a wave on the torus, an effect of one loop in a phase space and an effect of two loops cancel out. Because the phase space has a structure like a Mobius strip. Thus, Rw has properties like a wave function.
The shape of the torus is decided by the Hamiltonian H of the system. To describe many particles, we need a new position quantity. This is analogous with second quantization.
A point on the torus is an elementary state f (w, θ, x, t). We can count elementary states since a position quantity has a minimum unit. The number of elementary states N (θ, x, t) is
|
|
(3.3) |
where u is a minimum unit and f (w, θ, x, t) = 1.
4 Probability
The probability of quantum theory is the probability of an event. We consider only the number of different elementary events since we measure only one elementary event of many elementary events.
I suppose that
|
|
(4.1) |
and
|
|
(4.2) |
Then, we can obtain the number of different combinations of the elementary states, m2 since the time has minimum unit. The combinations are elementary events. If there are only m different elementary states, there are m2 different elementary events.
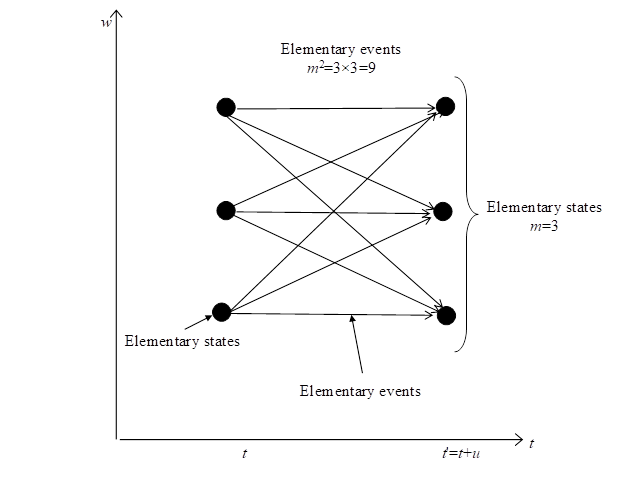
Figure 4-1: The number of elementary events is the square of the number of elementary states.
If there is a state ![]() , the
probability of finding a particle at the position x, P (x)
is
, the
probability of finding a particle at the position x, P (x)
is
|
|
(4.3) |
Thus, we can obtain the probability from this theory. Each elementary event exists. Thus, each observer measuring each elementary event exists, too. This is Many-Worlds Interpretation.
5 Conclusion
This theory provides the probability of quantum theory.