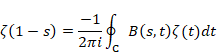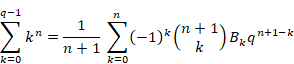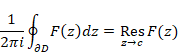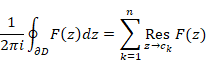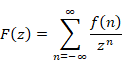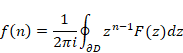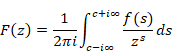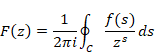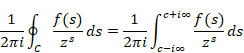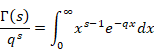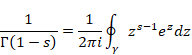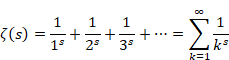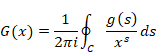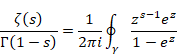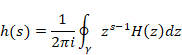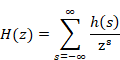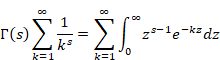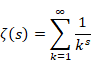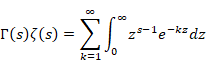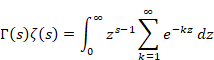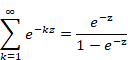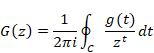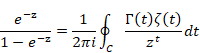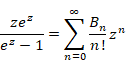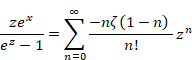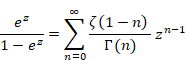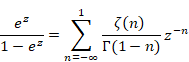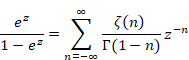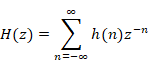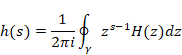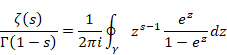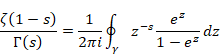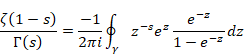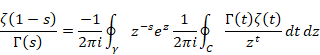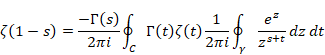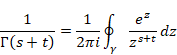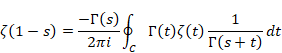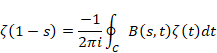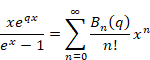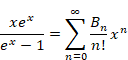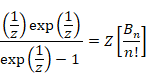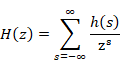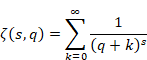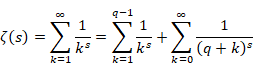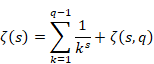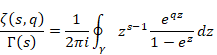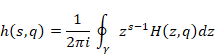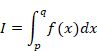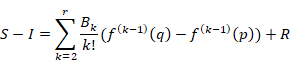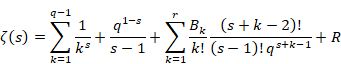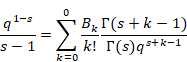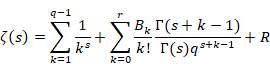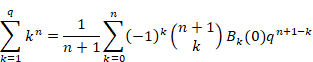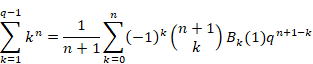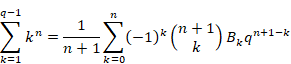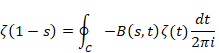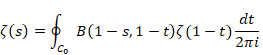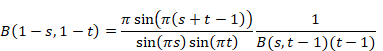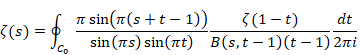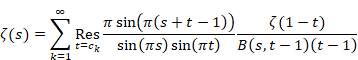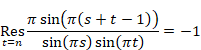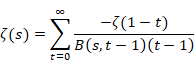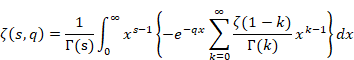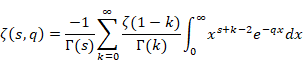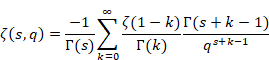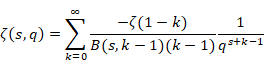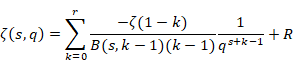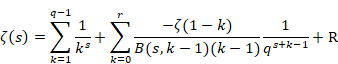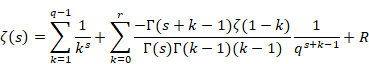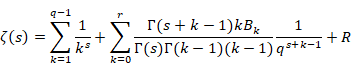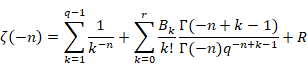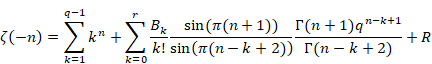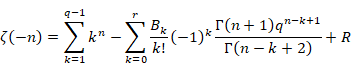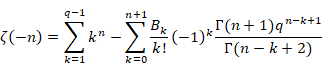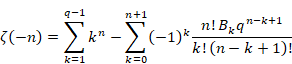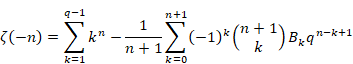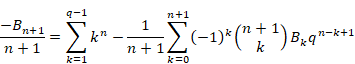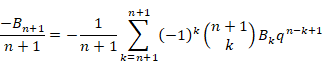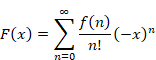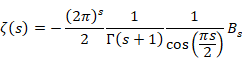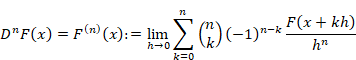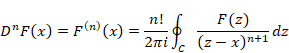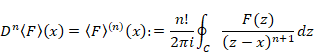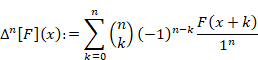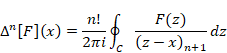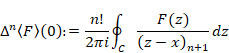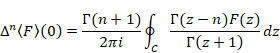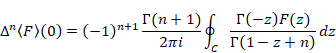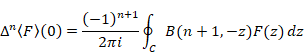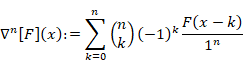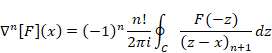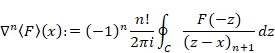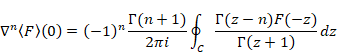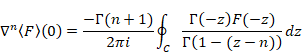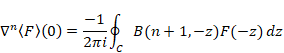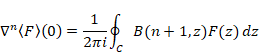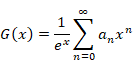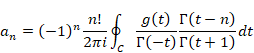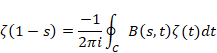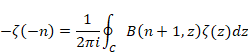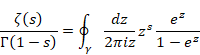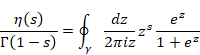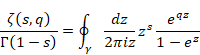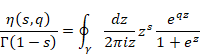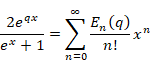このため、多くの数学者がリーマン予想の証明を試みてきた。しかし、それらの試みは成功していない。リーマン予想を証明する方法の一つは、ゼータ関数の零点を、ある作用素の固有値と解釈することである。しかし、これまで、その作用素は見つかっていなかった。反射積分方程式は、この作用素のひとつと考えられる。このため、反射積分方程式の導出は重要な課題である。

1.3 これまでの研究動向

レオンハルト・オイラーは、1737年にゼータ関数の無限級数を導入した。ベルンハルト・リーマンは、1859年にゼータ関数の解析接続を導入した。

ダフィット・ヒルベルトとゲオルグ・ポリア[2]は1914年頃に、ゼータ関数の零点は、ある作用素の固有値であろうと予想した。この予想はヒルベルト＝ポリア予想と呼ばれている。

ゼエフ・ルドニックとピーター・サルナック[3]は1996年にランダム行列理論で零点の分布を研究している。黒川重信氏は1996年頃より1元体[4]を研究している。アラン・コンヌ[5]は1998年に非可換幾何学とリーマン予想の関係を示した。クリストファー・デニンガー[6]は1998年に零点の固有値解釈を研究している。

1.4 本論文の新しい導出方法

(反射積分方程式)

(1.1)

反射積分方程式から、ファウルハーバーの公式とネールント=ライス積分を導出する。

(ファウルハーバーの公式)

(1.2)

2 既知の内容の確認

本章では、既知の内容を確認する。

2.1 コーシーの留数定理

オーギュスタン＝ルイ・コーシーは、1831年に留数定理[7]を発表した。

関数F (z)は単純閉曲線∂Dの内部の領域Dに孤立特異点cを持つほかは、領域Dの内部と周∂Dをこめて正則とする。このとき次の等式が成立する。

(留数定理)

(2.1)

関数F(z)が孤立特異点c_kを持つ場合は、次の等式が成立する。

(留数定理)

(2.2)

2.2 フレビッツのZ変換

ビトルド・フレビッツ[8]は1947年にZ変換を発表した。関数F(z)が領域D = {0<|z|<R}で正則ならば、その領域内で広義一様収束する級数に変換できる。

(Z変換)

	(2.3)
	(2.4)
	(2.5)

したがって、原点Oと極iRの最小距離がRのとき、Z変換の領域Dは次のとおり。白丸は極である。

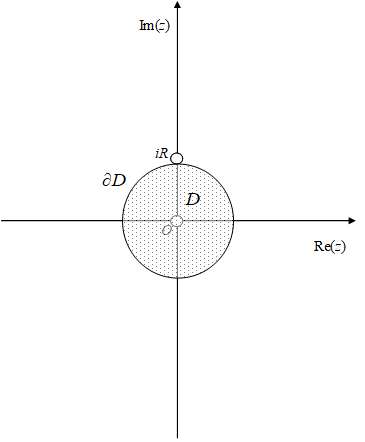
Z変換の領域

図 2-1: Z変換の領域

逆Z変換は、その領域Dを囲む積分経路∂Dの周回積分となる。

(逆Z変換)

	(2.6)
	(2.7)

2.3 メリン変換

ハジャルマー・メリン[9]は、1904年にメリン変換を発表した。

(メリン変換)

	(2.8)
	(2.9)

関数 f (s) が複素帯領域 S = {a < Re(s) < b} で正則で、 a と b の間にある任意の実数 c に対し Im(s) → ±∞ において f (s) → 0 ならば、次の線積分は絶対収束する。

(逆メリン変換)

	(2.10)
	(2.11)
	(2.12)

複素帯領域 S の実部は、被積分関数のすべての極の実部より大きい必要がある。複素帯領域 S を次の図に示す。白丸は極である。

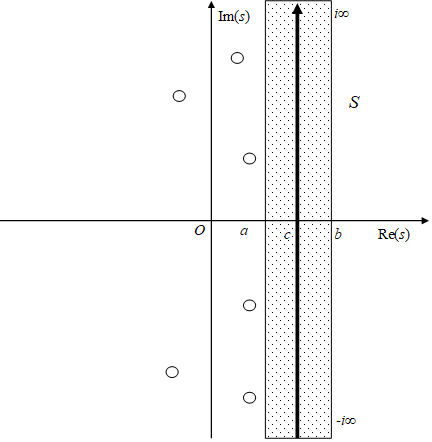
メリン逆変換の複素帯領域S

図 2-2: 逆メリン変換の複素帯領域S

逆メリン変換を周回積分で次のように定義する。

(逆メリン変換)

	(2.13)
	(2.14)

積分経路Cは被積分関数のすべての極を囲む経路とする。例として積分経路 C = C_I + C_Rを次のようにとる。白丸は極である。

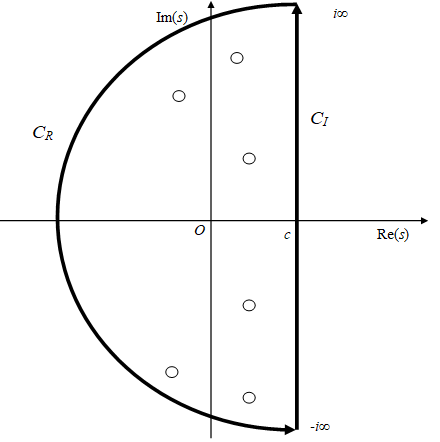
メリン逆変換の積分経路

図 2-3: 逆メリン変換

積分経路C_Rの線積分が0ならば、積分経路Cの周回積分は積分経路C_Iの線積分に一致する。そのとき、次の式が成立する。

(2.15)

2.4 オイラーのガンマ関数

レオンハルト・オイラー[10]は1729年に階乗の一般化としてガンマ関数を導入した。

(ガンマ関数)

(2.16)

変数xを(qx)に置き換え、次の公式を得る。

(2.17)

上記の式で(dx)は(qdx)に置き換えた。

ヘルマン・ハンケルは1863年に次の積分表示[11]を発表した。

(ガンマ関数の周回積分)

(2.18)

ガンマ関数の積分経路は次の図の経路γである。

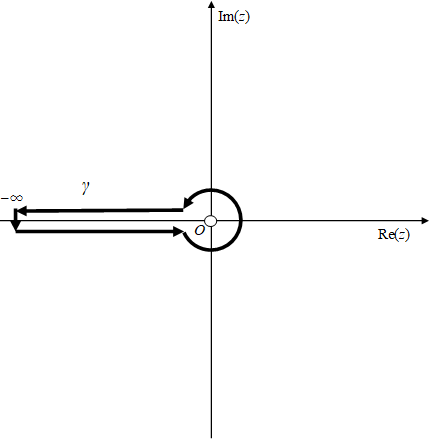
ガンマ関数の積分経路

図 2-4: ガンマ関数の積分経路

ガンマ関数は次の公式を持つ。

(ガンマ関数の反射公式)

(2.19)

上記の式は、オイラーの反射公式、相半公式、相反公式、相補公式とも呼ばれている。

2.5 オイラーのベータ関数

レオンハルト・オイラーは、1768年に彼の著書[12]でベータ関数を導入した。

(ベータ関数)

(2.20)

ガンマ関数の反射公式により、ベータ関数の反射公式を得る。

(ベータ関数の反射公式)

(2.21)

2.6 リーマンのゼータ関数

レオンハルト・オイラーは、1737年にゼータ関数の無限級数を導入した。

(ゼータ関数)

(2.22)

ベルンハルト・リーマン[13]は、1859年にゼータ関数をガンマ関数で表現した。

(ゼータ関数)

(2.23)

上記の式を次のメリン変換と解釈する。

(ゼータ関数のメリン変換)

	(2.24)
	(2.25)
	(2.26)
	(2.27)

その関数の逆メリン変換は次のとおりである。

(ゼータ関数の逆メリン変換)

	(2.28)
	(2.29)
	(2.30)
	(2.31)

ベルンハルト・リーマンは、1859年にゼータ関数の解析接続を導入した。

(ゼータ関数の解析接続)

(2.32)

上記の式を、式(2.7)のような逆Z変換と解釈する。

(ゼータ関数の逆Z変換)

	(2.33)
	(2.34)
	(2.35)
	(2.36)

積分経路γを次の図に示す。白丸は極を意味する。

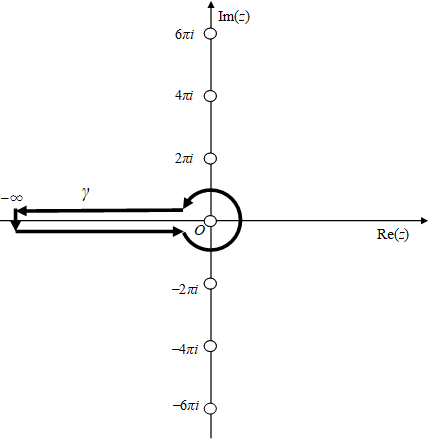
ゼータ関数の積分経路

図 2-5: ゼータ関数の積分経路

ゼータ関数のZ変換は次のとおり。

(Z変換)

	(2.37)
	(2.38)
	(2.39)
	(2.40)

メリン変換とZ変換の母関数は次の関係を持つ。

	(2.41)
	(2.42)

リーマンは次の公式を示した。

(リーマンの反射公式)

(2.43)

リーマンは1859年に次の予想を提唱した。

(リーマン予想)

非自明な零点の実数部はすべて1/2である。

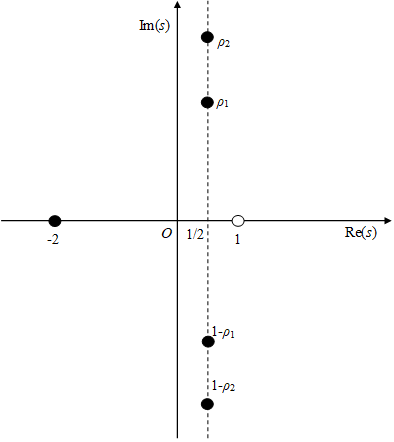
自明でない零点ρ₁とρ₂の例を次の図に示す。黒丸が零点、白丸は極である。

ゼータ関数の自明でない零点

図 2-6: ゼータ関数の自明でない零点

	(2.44)
	(2.45)

このリーマン予想の証明は、未解決であり、重要な課題となっている。

3 反射積分方程式の導出

本章では、次の積分方程式を証明する。

(ゼータ関数の積分方程式)

(3.1)

証明

導出方法の枠組みは次のとおり。

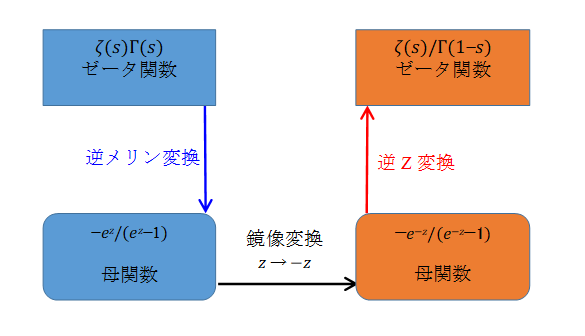
導出方法の枠組み

図 3-1: ゼータ関数の積分方程式導出の枠組み

一方、ガンマ関数は次の通り。

(3.2)

変数zをkzに置き換え、dzをkdzに置き換える。

(3.3)

両辺について、k = 1から無限大までの和を取る。

(3.4)

左辺を次のゼータ関数で置き換える。

(3.5)

その結果、次の式を得る。

(3.6)

右辺の和と積分の順序を入れ替える。

(3.7)

ここで次の等比級数の公式を用いる。

(3.8)

その結果、次の式を得る。

(3.9)

上記の式は次のようなメリン変換と解釈できる。

(3.10)

したがって、次のような逆メリン変換が可能である。

(3.11)

その結果、次の式を得る。

(3.12)

逆メリン変換では、積分経路Cは被積分関数のすべての極を囲む必要がある。そこで積分経路Cを次のように取る。白丸は極である。

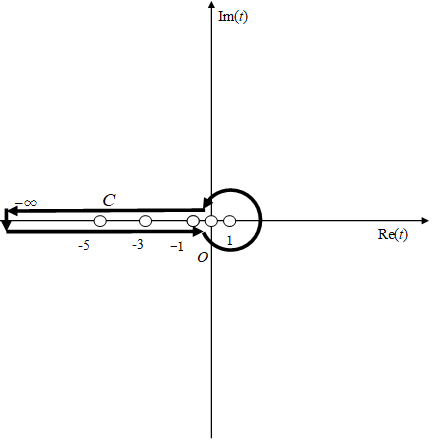
メリン逆変換の積分経路

図 3-2: 逆メリン変換の積分経路

ここで、ベルヌーイ数は次の通り。

(3.13)

一方、ゼータ関数とベルヌーイ数には次の関係がある。

(3.14)

上記の式を式(3.13)に代入する。

(3.15)

階乗をガンマ関数に置き換え、変形する。

(3.16)

nを1−nに置き換える。

(3.17)

2以上の自然数nに対し次の値は0になる。

(3.18)

そのため、式(3.19)は次のように和を取る範囲を無限大まで延長できる。

(3.19)

上記の式は次のようなZ変換と解釈できる。

(3.20)

したがって、次のような逆Z変換が可能である。

(3.21)

その結果、次の式を得る。

(3.22)

積分経路 γ は次の図のとおり。白丸は極を意味する。

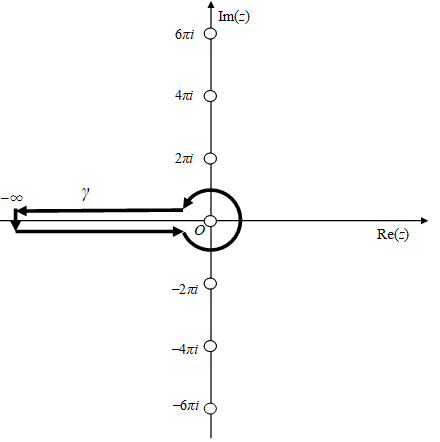
ゼータ関数の積分経路

図 3-3: ゼータ関数の積分経路

sを1−sに置き換える。

(3.23)

ここで次の式を用いる。

(3.24)

その結果、次の式を得る。

(3.25)

上記の式に、次の式(3.12)を代入する。

(3.12)

その結果、次の式を得る。

(3.26)

変形する。

(3.27)

一方、ガンマ関数にはハンケルの積分表示がある。下記式を上記の式に代入する。

(3.28)

その結果、次の式を得る。

(3.29)

次のベータ関数を使い、整理する。

(3.30)

この結果、次の式を得る。

(3.31)

上記が求めたい積分方程式だった。(証明終了)

∎

4 結論

本論文では、次の結果を得た。

・ゼータ関数の反射積分方程式を導出した。

5 今後の課題

今後の課題は次のとおり。

・ファウルハーバーの公式を導出する。

・ネールント=ライス積分を導出する。

・反射積分方程式の固有値を調べる。

6 補足1: ファウルハーバーの公式の導出

補足では、既知の内容を確認後、次の式を導出する。

・ファウルハーバーの公式

6.1 既知の内容の確認 (その2)

本節では、既知の内容を確認する。

6.1.1 ベルヌーイ多項式

ベルヌーイ多項式を次のように定義する。

(ベルヌーイ多項式)

(6.1)

上記の級数は全領域で収束しない。原点と母関数の極の最小距離が2πのため、収束半径は2πである。

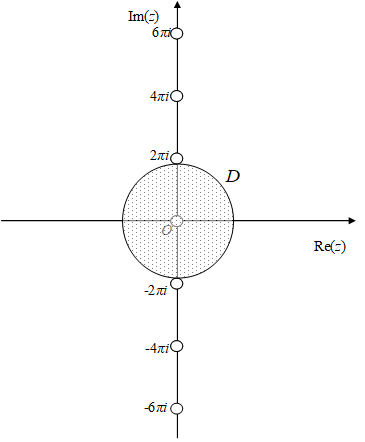
ベルヌーイ多項式の級数の収束半径

図 6-1: ベルヌーイ多項式の級数の収束半径

6.1.2 ベルヌーイ数

ヤコブ・ベルヌーイは1713年に彼の著書[14]で、ベルヌーイ数を導入した。

(ベルヌーイ数)

(6.2)

正の偶数 n に対し、次の公式が成立する。

(ベルヌーイ数の反射公式)

(6.3)

ヴィーフの著書[15]によれば、次のZ変換が存在する。

(ベルヌーイ数のZ変換)

(6.4)

本論文では、次のZ変換を使用する。

(ベルヌーイ数のZ変換)

	(6.5)
	(6.6)
	(6.7)
	(6.8)

一方、ゼータ関数のZ変換は次の通り。

(ゼータ関数のZ変換)

	(6.9)
	(6.10)
	(6.11)
	(6.12)

したがって、次の式が成立する。

(6.13)

変数sを負の整数-nに置換し、次の公式を得る。

(ベルヌーイ数の公式)

(6.14)

従来、ベルヌーイ数は離散的であると考えられてきた。私は、ベルヌーイ数は連続的であると考える。連続的なベルヌーイ数をベルヌーイ関数と呼ぶ。私はベルヌーイ関数をゼータ関数の次のような異なる表現と解釈する。

(6.15)

6.1.3 フルヴィッツのゼータ関数

アドルフ・フルヴィッツ[16]は1882年に、次のゼータ関数を導入した。

(フルヴィッツのゼータ関数)

(6.16)

フルヴィッツのゼータ関数とリーマンのゼータ関数の関係を次に示す。

	(6.17)
	(6.18)

フルヴィッツのゼータ関数はq が1に等しいとき、リーマンのゼータ関数となる。

(6.19)

フルヴィッツのゼータ関数をガンマ関数で表現する。

(フルヴィッツのゼータ関数)

(6.20)

上記の式を次のメリン変換と解釈する。

(メリン変換)

	(6.21)
	(6.22)
	(6.23)
	(6.24)

フルヴィッツのゼータ関数の解析接続は次の通り。

(フルヴィッツのゼータ関数の解析接続)

(6.25)

上記の式を、次の逆Z変換と解釈する。

(逆Z変換)

	(6.26)
	(6.27)
	(6.28)
	(6.29)

自然数nに対し、次の等式が成立する。

(ベルヌーイ多項式の公式)

(6.30)

6.1.4 オイラー=マクローリンの和公式

オイラー[17]は1738年に次の公式を発見した。マクローリン[18]も1742年に、オイラーとは独立に同式を発見している。

(オイラー=マクローリンの和公式)

	(6.31)
	(6.32)
	(6.33)

上記の式において、変数Rは誤差項である。

6.1.5 漸近展開

オイラー[19]は1755年にオイラー＝マクローリンの和公式でゼータ関数の値を計算している。

(ゼータ関数の漸近展開)

(6.34)

上記の式において変数Rは誤差項である。導出方法の詳細は、エドワーズ[20]の1974年の著書にある。

ここで次の等式を用いる。

(6.35)

その結果、次の式を得る。

(ゼータ関数の漸近展開)

(6.36)

6.1.6 ファウルハーバーの公式

ヨハン・ファウルハーバー[21]は1631年にべき乗和の公式を提示した。自然数nに対し次の公式が成立する。

(ファウルハーバーの公式)

(6.37)

上記の式をベルヌーイ多項式B_k(1)で表現する。

(ファウルハーバーの公式)

(6.38)

本論文では、上記の式をベルヌーイ数B_kで次のように表現する。

(ファウルハーバーの公式)

(6.39)

6.2 ファウルハーバーの公式の導出

ファウルハーバーの公式を導出するため、次の公式を導出する。

- リーマンのゼータ関数の総和方程式

- フルヴィッツのゼータ関数の総和方程式

- リーマンのゼータ関数の漸近展開

6.2.1 リーマンのゼータ関数の総和方程式の導出

リーマンのゼータ関数の総和方程式を導出する。

反射積分方程式は次のとおり。

(反射積分方程式)

(6.40)

上記の式において、変数 s を (1-s) に置き換え、変数 t を (1-t) に置き換える。

(反射積分方程式)

(6.41)

積分経路 C₀を次の図に示す。白丸は極である。

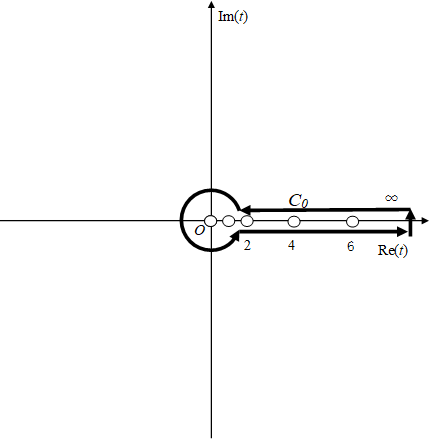
ゼータ関数の周回積分方程式の積分経路

図 6-2:反射積分方程式の積分経路

上記の式に次の式を代入する。

(ベータ関数の反射公式)

(6.42)

その結果、次の式を得る。

(6.43)

上記の式を留数定理で積分する。

(6.44)

ここで、 c_kは k 番目の特異点である。特異点は 0, 1, 2, 4, 6, … である。

整数 n に対し次の等式が成り立つ。

(6.45)

すべての特異点は整数であり、ゼータ関数 ζ (1-t) の値は t = 3, 5, 7, … で零であるため、次のように書ける。

(総和方程式)

(6.46)

上記の式は発散するため、計算できない。この問題を解決するため、次の節で、フルヴィッツのゼータ関数の総和方程式を導出する。

6.2.2 フルヴィッツのゼータ関数の総和方程式の導出

この節では、フルヴィッツのゼータ関数の総和方程式を導出する。

フルヴィッツのゼータ関数は次の通り。

(フルヴィッツのゼータ関数)

(6.47)

上記の式をメリン変換の母関数で次のように表現する。

(6.48)

上記の式は次のように変形できる。

(6.49)

上記の式の関数H(x)にゼータ関数のZ変換を代入すると下記となる。

	(6.50)
	(6.51)

そのZ変換は領域Dで収束する。したがって、その領域で、積分と総和の順序を変更できる。

変数 x について積分するため、次のように式を整理する。

(6.52)

この式に、次のガンマ関数の等式(2.17)を適用する。

(6.53)

その結果、次の式が得られる。

(6.54)

ここで、次のベータ関数(2.20)を利用して式を簡略化する。

(6.55)

すると下記式となる。

(フルヴィッツのゼータ関数の総和方程式)

(6.56)

「ベルヌーイ関数の級数定義式」は収束半径が2πのため、上記の式は発散する。そのため、総和の上限値を変数qに依存する変数rに変更する。

(フルヴィッツのゼータ関数の総和方程式)

(6.57)

ここでRは誤差項である。

6.2.3 漸近展開の導出

本節ではゼータ関数の漸近展開(6.36)を導出する。

リーマンとフルヴィッツのゼータ関数の関係は次の通り。

(6.58)

したがって、リーマンのゼータ関数の総和方程式は次のように表現できる。

(総和方程式)

(6.59)

ベータ関数をガンマ関数に置き換えると下記式を得る。

(6.60)

ベルヌーイ多項式の等式により次のように変形する。

(6.61)

上記の式を変形し、ゼータ関数の漸近展開を得る。

(ゼータ関数の漸近展開)

(6.62)

6.2.4 ファウルハーバーの公式の導出

本節ではファウルハーバーの公式を導出する。

ゼータ関数の漸近展開(6.36)は次の通り。

(ゼータ関数の漸近展開)

(6.63)

上記の式において、変数sを(-n)に置き換える。

(6.64)

上記の式に、オイラーの反射公式を適用し次の式を得る。

(6.65)

整数kに対し次の等式が成り立つ。

(6.66)

したがって、次の式を得る。

(6.67)

自然数n、整数k > n+1に対し次の式が成立する。

(6.68)

したがって、次の式が成立する。

(6.69)

k > n+1の項の値がすべてゼロであるため、誤差項Rを消し、式(6.67)の総和の上限をn+1に変更する。

(6.70)

上記の式を階乗記号で次のように表現する。

(6.71)

二項係数で次のように表現する。

(6.72)

ベルヌーイ多項式の等式により次のように変形する。

(6.73)

自然数n、整数k = n+1に対し次の式が成立する。

(6.74)

その結果、次の式が成立する。

(6.75)

したがって、式(6.73)を次のように変形し、ファウルハーバーの公式を得る。

(ファウルハーバーの公式)

(6.76)

上記の式が、本節で導出したい式であった。

7 補足2: ゼータ関数の平均後退差分によるゼータ関数の表現

7.1 既知の内容の確認(その3)

本節では、既知の内容を確認する。

7.1.1 ラマヌジャンの主定理

シュリニヴァーサ・ラマヌジャンは1910年ごろに実数xと複素数sに対し次の定理を得た[22]。

(ラマヌジャンの主定理)

	(7.1)
	(7.2)

上記の式は次のベルヌーイ数とゼータ関数で成立する。

	(7.3)
	(7.4)
	(7.5)

この定理は次の関係式を示唆している。

(7.6)

7.1.2 ウーンの連続的なベルヌーイ数

ウーン [23]は1997年に、連続的なベルヌーイ数を導入した。

自然数nに対し、次の公式が成立する。

(ベルヌーイ数の公式)

(7.7)

ウーンは複素数sに対し次の等式を提案した。

(ベルヌーイ関数の等式)

(7.8)

本論文では、ベルヌーイ数の従来の表記法に基づき、ベルヌーイ関数に対し次の表記法を用いる。

(ベルヌーイ関数の等式)

(7.9)

上記の式をリーマンの反射公式に代入し、次の式を得る。

(7.10)

上記の式を変形することで次の式を得る。

(ベルヌーイ関数の反射公式)

(7.11)

上記の式は正の偶数 s に対し、下記式となる。

(7.12)

上記の式は、正の偶数 n に対する次の式と等しい。

(ベルヌーイ数の反射公式)

(7.13)

上記の結果は、ベルヌーイ関数の等式の妥当性を示唆する。

7.1.3 コーシーの積分公式

微分は次のように定義される。

(7‑14)

2階微分は次のように定義される。

(7‑15)

n階微分は次のように定義される。

(7‑16)

ここで、は二項係数である。

(7‑17)

関数F(z)が経路C内で正則の場合、n階微分はコーシーの積分公式で表現できる。

(コーシーの積分公式)

(7‑18)

関数F(z)が経路C内で正則でない場合、n階微分はコーシーの積分公式で表現できない。関数F(z)を経路Cで平均した関数f(z)の微分が得られる。平均化した微分であるため、新しい記号で表現する。

(コーシーの平均微分公式)

(7‑19)

7.1.4 ネールント=ライス積分

前進差分は次のように定義される。

(7‑20)

2階前進差分は次のように定義される。

(7‑21)

n階前進差分は次のように定義される。

(7‑22)

正則の場合、n階前進差分はネールント=ライス積分で表現できる。

(ネールント=ライス積分)

(7‑23)

ここで (z−x)_n₊₁は下降階乗である。

(7‑24)

ネールント=ライス積分はニールス・エリク・ネールントが1924年にを発表した[24]。

関数F(z)が経路C内で正則でない場合、n階前進差分はネールント=ライス積分(7‑23)で表現できない。関数F(z)を経路Cで平均した関数の差分が得られる。平均化した前進差分であるため、新しい記号で表現する。

(ネールント=ライス平均前進差分公式)

(7‑25)

x=0とし、階乗と下降階乗をガンマ関数で表現する。

(7‑26)

ガンマ関数の反射公式より次の式が成り立つ。

	(7‑27)
	(7‑28)

したがって式(7‑27)を式(7‑28)で割ることにより、次の式が成り立つ。

(7‑29)

ここで、次の式が成り立つ。

(7‑30)

したがって、式(7‑29)は次のようになる。

(7‑31)

したがって、式(7‑26)は次のようになる。

(7‑32)

ガンマ関数をベータ関数で表現する。

(ネールント=ライス平均前進差分公式)

(7‑33)

7.1.5 ネールント=ライス積分(後退差分)

後退差分は次のように定義される。

(7‑34)

2階後退差分は次のように定義される。

(7‑35)

n階後退差分は次のように定義される。

(7‑36)

関数F(z)が経路C内で正則の場合、n階後退差分はネールント=ライス積分で表現できる。

(ネールント=ライス積分)

(7‑37)

ここで (z−x)_n₊₁は下降階乗である。

(7‑38)

関数F(z)が経路C内で正則でない場合、n階後退差分はネールント=ライス積分(7‑37)で表現できない。関数F(z)を経路Cで平均した関数f(z)の差分が得られる。平均化した後退差分であるため、新しい記号で表現する。

(ネールント=ライス平均後退差分公式)

(7‑39)

ここでx=0とし階乗と下降階乗をガンマ関数で表現する。

(7‑40)

ガンマ関数の反射公式より次の式が成り立つ。

	(7‑41)
	(7‑42)

したがって式(7‑41)を式(7‑42)で割ることにより、次の式が成り立つ。

(7‑43)

ここで、次の式が成り立つ。

(7‑44)

したがって、式(7‑43)はつぎのようになる。

(7‑45)

したがって、式(7‑40)はつぎのようになる。

(7‑46)

ガンマ関数をベータ関数で表現する。

(ネールント=ライス平均後退差分公式)

(7‑47)

zを-zに置き換える。

(ネールント=ライス平均後退差分公式)

(7‑48)

7.1.6 ポアソン＝メリン＝ニュートン循環

ネールント=ライス積分に関連し、フラジョレットは1985年にポアソン＝メリン＝ニュートン循環を発表した[25]。

(ポアソン＝メリン＝ニュートン循環)

	(7.49)
	(7.50)
	(7.51)

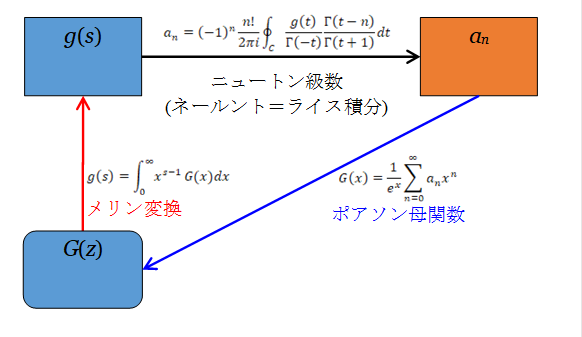
ポアソン-メリン-ニュートンサイクル

図 7-1: ポアソン＝メリン＝ニュートン循環

7.2 ゼータ関数の平均後退差分によるゼータ関数の表現

ゼータ関数の平均後退差分はゼータ関数と等しい。

(7‑52)

証明

ゼータ関数の反射積分方程式より下記が成立する。

(7‑53)

両辺に－1をかけ、複素数1－sを－nとする。

(7‑54)

上記の式(7‑54)の右辺をネールント=ライス平均後退差分公式(7‑48)の右辺と比較し次の式を得る。

(7‑55)

上記が求めたい式であった。(証明終了)

■

ゼータ関数では平均後退差分は、通常の後退差分で次のように表現できる。

(7‑56)

ネールント＝ライス積分は前進差分でも定義可能だが、前進差分では上記のようにゼータ関数を簡潔に表現できない。計算過程を省略し結果だけを記すと下記となる。

	(7‑57)
	(7‑58)

ここで、は平均前進差分であり、は通常の前進差分である。

8 付録

8.1 逆Z変換表

逆Z変換表は次のとおり。

表 8‑1:逆Z変換表

#			番号
1			(8.1)
2			(8.2)
3			(8.3)
4			(8.4)

上記の関数は次のとおり。

(リーマンのゼータ関数)

(8.5)

(ディリクレ[26]のイータ関数)

(8.6)

(フルヴィッツのゼータ関数)

(8.7)

(フルヴィッツのイータ関数)

(8.8)

多項式の公式は次のとおり。

	(8.9)
	(8.10)
	(8.11)
	(8.12)

多項式の定義は次のとおり。

(ベルヌーイ多項式)

(8.13)

(オイラー多項式)

(8.14)