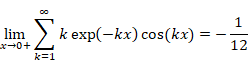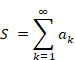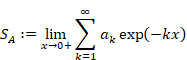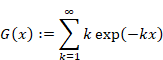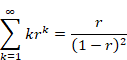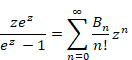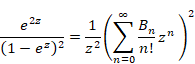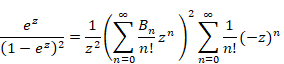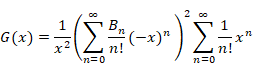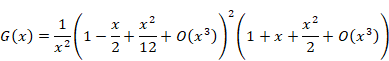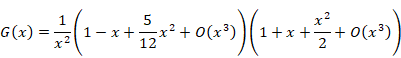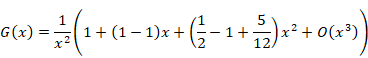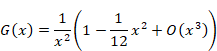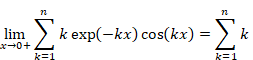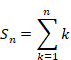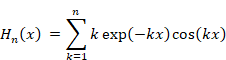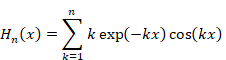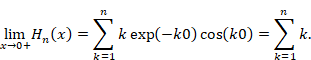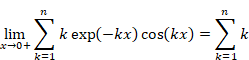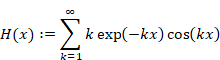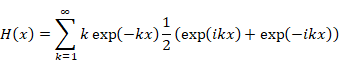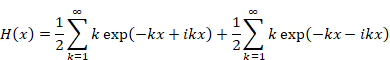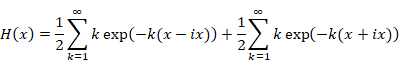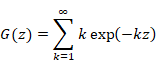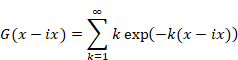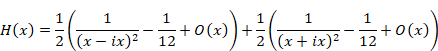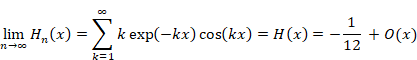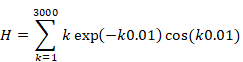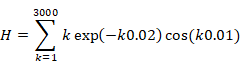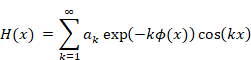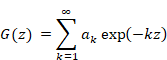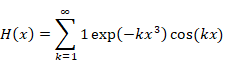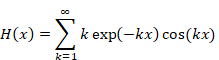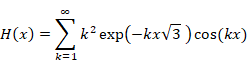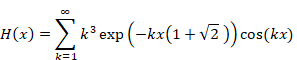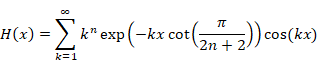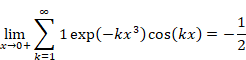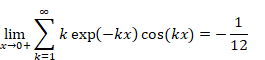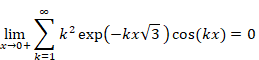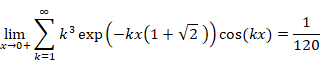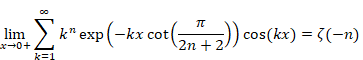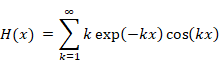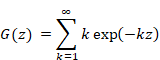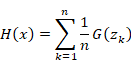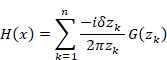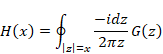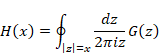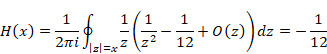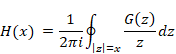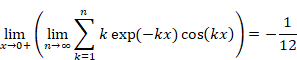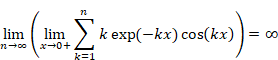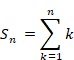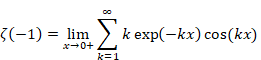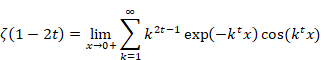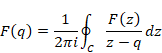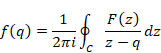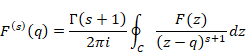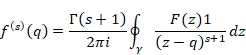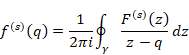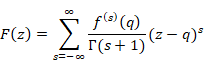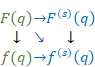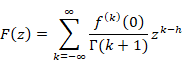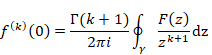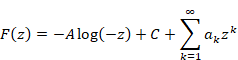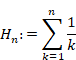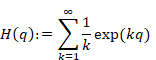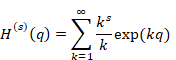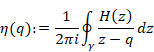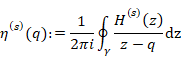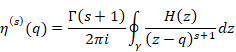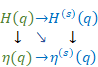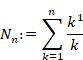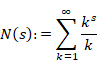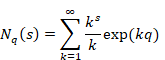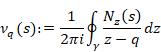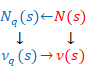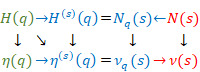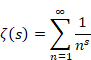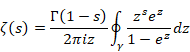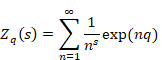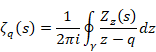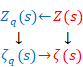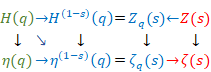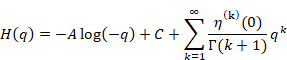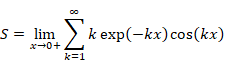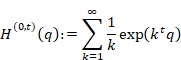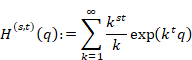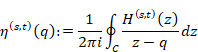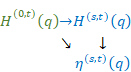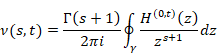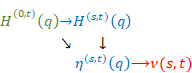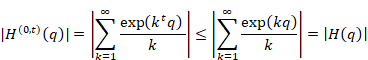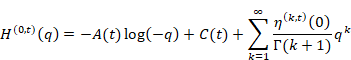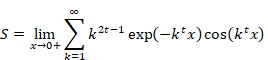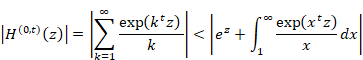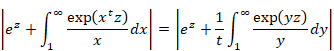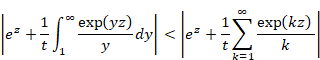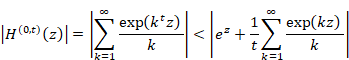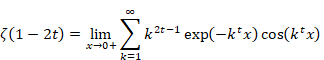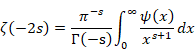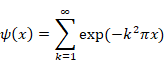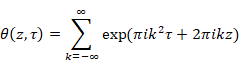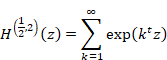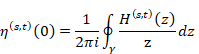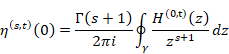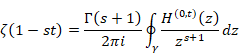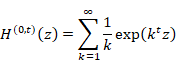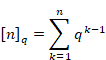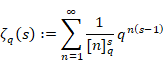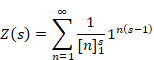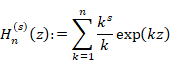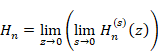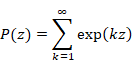自然数の総和がゼータ関数の-1/12であることの新しい証明
ホーム > 量子力学 > ゼータ関数とベルヌーイ数
2022/04/16
公開日 2014/3/30
K. Sugiyama[1]
ゼータ関数の自然数和Z(-1)=1+2+3+…は発散する。一方、ゼータ関数の解析接続ζ(-1)=”1+2+3+…” は-1/12に収束することが知られている。自然数の和はどのようにして-1/12に近づいてゆくのだろうか?
本論文では、自然数和が増加したあと減少に転じ-1/12に収束することを証明する。
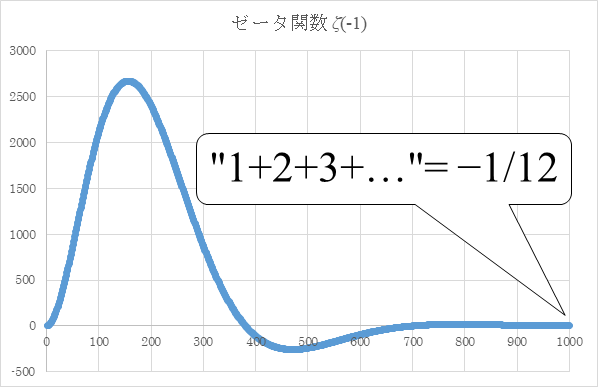
図 5.1: 自然数和の減衰振動
アーベルは発散級数の和をアーベル総和法で計算した。しかし、自然数の総和はアーベル総和法を使っても発散する。本論文は、減衰振動するアーベル総和法で自然数の総和を計算する。
目次
6.1.7 平均調和倍音導関数による自然数のべき乗和の公式の証明
1 序論
1.1 課題
ゼータ関数の自然数和は発散する。
|
|
(1‑1) |
一方、ゼータ関数の解析接続は収束する。
|
|
(1‑2) |
自然数の和はどのようにして-1/12に近づいてゆくのだろうか?通常のゼータ関数Z(s)がゼータ関数の解析接続ζ(s)に変わるとき、何が起きるのだろうか?
収束の仕組みを調べるため、自然数和をアーベル総和法で計算してみよう。
自然数の通常和は次のように表現できる。
(自然数の通常和)
|
|
(1‑3) |
アーベル総和法では次のように、各自然数に、減衰する指数関数をかけて和を取る。
(自然数和のアーベル総和法)
|
|
(1‑4) |
上記の式を計算すると、次の式を得ることができる。
|
|
(1‑5) |
しかし残念なことに、上記の式は最初の項1/x2 が発散している。従って、自然数の総和はアーベル総和法を使っても発散する。
この発散を除くことが本論文の目的である。本論文は、減衰振動するアーベル総和法で自然数の総和を計算する。
1.2 これまでの研究動向
レオンハルト・オイラーが、1749年に自然数の総和が -1/12 になることを示唆した[2]。ベルンハルト・リーマンは1859年に、ゼータ関数 ζ(-1) の積分表示が -1/12 であることを示した[3]。シュリニヴァーサ・ラマヌジャンは1913年にラマヌジャン総和法で自然数の総和が -1/12 になると主張した[4]。
ニールス・アーベル[5]は発散級数を収束させるため、1829年頃にアーベル総和法を導入した。佐藤潤也氏は、1989年にゼータ関数のq類似を導入した[6]。金子昌信氏と黒川信重氏、若山正人氏は、2002年にゼータ関数のq類似で二重引用符付きの自然数和を導出した[7]。
1.3 本論文の新しい導出方法
新しい自然数の総和を、新しい総和法、振動アーベル総和法(減衰振動総和法)で定義する。その方法は、非常にゆっくり減衰し振動する収束因子を発散級数にかけ収束させる。無限項では、通常の総和は発散する。一方、その新しい和は、有限項では従来の和と等しい。そして、その和は、無限項では -1/12 に収束する。
(自然数和の公式)
|
|
(1‑6) |
1.4 アーベル総和法による古い方法
アーベルは1829年頃にアーベル総和法を導入した。次の級数の総和を考える。
|
|
(1‑7) |
このとき、アーベル和は次のように定義できる。
|
|
(1‑8) |
|
|
(1‑9) |
アーベルは発散級数の和をアーベル総和法で計算した。しかし、自然数の総和はその方法で計算できない。その理由を次に説明する。
次の自然数の総和を考える。
|
|
(1‑10) |
このとき、次の関数を定義する。
|
|
(1‑11) |
|
|
(1‑12) |
ここで、次の公式を使用する。
(自然数の係数を持つ等比級数の公式)
|
|
(1‑13) |
上記の公式より次の式を得る。
|
|
(1‑14) |
アーベル和は次のように計算できる。
|
|
(1‑15) |
上記のように、自然数のアーベル和は発散する。そのため、自然数の総和はアーベル和で計算できない。この発散の様子をもう少し詳しく調べるため、次のベルヌーイ数の定義式を利用する。
(ベルヌーイ数の定義式)
|
|
(1‑16) |
本論文では、ベルヌーイ数 Bn はベルヌーイ多項式 Bn (1)とする。上記の式の両辺を2乗する。そして両辺をz2でわる。すると下記式を得る。
|
|
(1‑17) |
上記の式の左辺にe-zをかける。そして右辺にe-zのマクローリン級数をかける。すると下記式を得る。
|
|
(1‑18) |
したがって、関数G (x)は次のように表現できる。
|
|
(1‑19) |
上記の式を計算し、下記式を得る。
|
|
(1‑20) |
|
|
(1‑21) |
|
|
(1‑22) |
|
|
(1‑23) |
|
|
(1‑24) |
ここで、記号O (x) はランダウの記号である。その記号は、誤差が変数 x のオーダーであることを意味する。第1項は発散している。第1項は特異項と呼ばれている。このため、次のアーベル和は発散する。
|
|
(1‑25) |
この発散を除くことが本論文の目的である。
2 新しい方法
2.1 自然数和の公式の新しい証明
本節は自然数和の公式の新しい証明を説明する。
次の命題が成立する。この命題は次節で証明する。
命題 1.
|
|
(2‑1) |
次の命題が成立する。この命題も次節で証明する。
命題 2.
|
|
(2‑2) |
関数 Sn (x) と Hn (x) を次のように定義する。
|
|
(2‑3) |
|
|
(2‑4) |
ここで次の記号を定義する。
|
|
(2‑5) |
|
|
(2‑6) |
|
|
(2‑7) |
|
|
(2‑8) |
すると次の命題が成立する。
|
|
(2‑9) |
|
|
(2‑10) |
|
|
(2‑11) |
二重引用符は、自然数和の解析接続を意味する。
無限項では、通常の総和は発散する。一方、その新しい和は、有限項では従来の和と等しい。そして、その和は、無限項では-1/12に収束する。
2.2 命題1の証明
命題1.
|
|
(2‑12) |
証明.
関数 Hn (x) を次のように定義する。
|
|
(2‑13) |
一方、次の式が成立する。
|
|
(2‑14) |
したがって、次の式が成立する。
|
|
(2‑15) |
(証終)
2.3 命題2の証明
命題2.
|
|
(2‑16) |
証明.
次の自然数の総和を考える。
|
|
(2‑17) |
このとき、次の関数を定義する。
|
|
(2‑18) |
|
|
(2‑19) |
ここで次の公式を使う。
(オイラーの公式)
|
|
(2‑20) |
上記の式より下記式を得る。
|
|
(2‑21) |
上記の式より θ = k x とおいて下記式を得る。
|
|
(2‑22) |
したがって、関数H(x)は次のように表現できる。
|
|
(2‑23) |
|
|
(2‑24) |
|
|
(2‑25) |
|
|
(2‑26) |
ここで、次の関数を定義する。
|
|
(2‑27) |
|
|
(2‑28) |
式(1‑24)より、関数G (z) は次のように表現できる。
|
|
(2‑29) |
したがって、関数 G (x - ix) は次のように表現できる。
|
|
(2‑30) |
|
|
(2‑31) |
すると、関数H(x)は次のように表現できる。
|
|
(2‑32) |
|
|
(2‑33) |
|
|
(2‑34) |
第1項は次のとおり。
|
|
(2‑35) |
一方、第2項は次のとおり。
|
|
(2‑36) |
そのため、第1項と第2項の和はゼロになる。
|
|
(2‑37) |
特異項がゼロとなったため、次の式が成立する。
|
|
(2‑38) |
関数 Hn (x) は次のように表現できる。
|
|
(2‑39) |
一方、式(2‑38)より次の式が成立する。
|
|
(2‑40) |
したがって、次の式が成立する。
|
|
(2‑41) |
(証終)
3 結論
本論文では、次の結果を得た。
- 自然数の総和がゼータ関数の値、-1/12であることを新しい方法で証明した。
4 今後の課題
今後の課題は次のとおり。
- 振動アーベル総和法とq類似との関連を調べる。
5 補足
5.1 振動アーベル総和法の数値計算
次の値を数値的に計算する。
|
|
(5‑1) |
|
|
(5‑2) |
この値は、次の -1/12 と非常に近い。
|
|
(5‑3) |
グラフでは次の図 5.1のとおり。
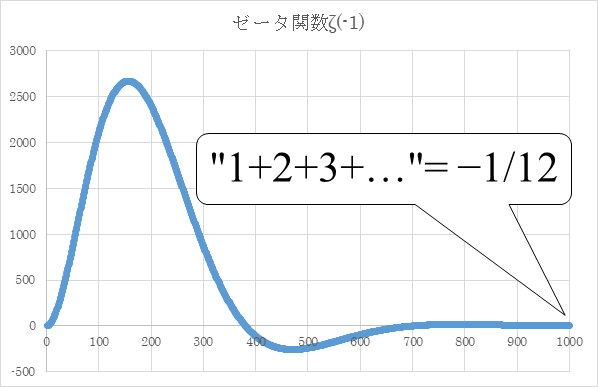
図 5.1: 自然数和の減衰振動
ここで、次のように減衰率を2倍にする。振動周期は変更しない。
|
|
(5‑4) |
|
|
(5‑5) |
したがって、減衰率と振動周期がある特別な関係を持たない場合、級数は収束しない。その関係を次の節で考察する。
5.2 振動アーベル総和法の一般公式
次の級数を考える。
|
|
(5‑6) |
このとき、次の関数を定義する。
|
|
(5‑7) |
|
|
(5‑8) |
|
|
(5‑9) |
また、次の関数を定義する。
|
|
(5‑10) |
|
|
(5‑11) |
関数G (z)は、特異項A (z)、定数項Cで次のように表現できる。
|
|
(5‑12) |
ここで次の公式を使う。
(オイラーの公式)
|
|
(5‑13) |
上記の公式により関数 H (x) は次のように表現できる。
|
|
(5‑14) |
|
|
(5‑15) |
|
|
(5‑16) |
関数G (z)の式(5‑12)より、次の式を得る。
|
|
(5‑17) |
上記の式の特異項を消去するためには、次の特異方程式で関数
![]() を決定する必要がある。
を決定する必要がある。
(特異方程式)
|
|
(5‑18) |
級数 a k と関数 G (z)、 ![]() を次に示す。
を次に示す。
|
級数 |
関数 |
関数 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
級数と振動アーベル総和法の例を次に示す。
|
級数 |
振動アーベル総和法の例 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
したがって、次の式が成立する。
|
|
(5‑19) |
|
|
(5‑20) |
|
|
(5‑21) |
|
|
(5‑22) |
上記の式は次のように計算する。
|
|
(5‑23) |
|
|
(5‑24) |
|
|
(5‑25) |
|
|
(5‑26) |
振動アーベル総和法の一般公式は次の通り。
|
|
(5‑27) |
|
|
(5‑28) |
5.3 平均アーベル総和法
次の自然数の総和を考える。
|
|
(5‑29) |
このとき、次の関数を定義する。
|
|
(5‑30) |
|
|
(5‑31) |
関数 H (x) は次のように表現できる。
|
|
(5‑32) |
上記の式は、次の図 5.2のような関数 G (z1) と G (z2) の和と解釈できる。
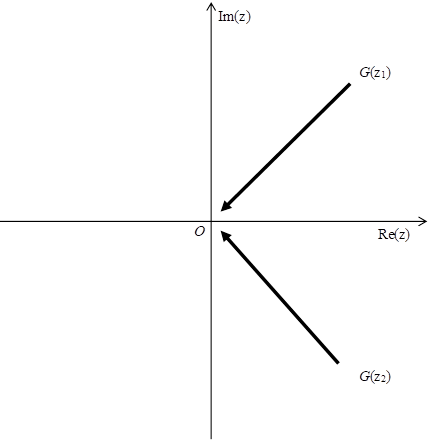
図 5.2: 振動アーベル総和法
上記の図 5.2では、2個の関数 G (z1) と G (z2) は2つの角度から原点Oに近づいている。これは特殊な条件である。その条件をもっと一般的にすることは可能だろうか?
そこで、次の図 5.3のように多くの関数 G (z) が、半径 x の円上のすべての点から原点Oに近づく場合を考察する。
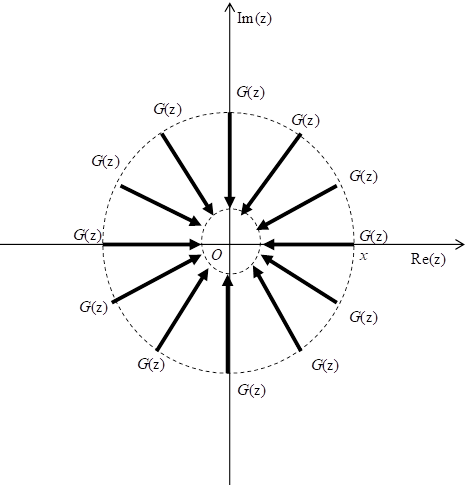
図 5.3:平均アーベル総和法
上記の考え方は、次の式で表現できる。
|
|
(5‑33) |
|
|
(5‑34) |
|
|
(5‑35) |
|
|
(5‑36) |
|
|
(5‑37) |
関数 H (x) は関数 G (z) の平均値である。
半径xの円の円周をLとする。円周Lは次のように表現できる。
|
|
(5‑38) |
一方、円周Lは十分大きいnに対し近似的に次のように表現できる。
|
|
(5‑39) |
したがって、次の等式が成立する。
|
|
(5‑40) |
ゆえに、規格化定数 1/n は次のように表現できる。
|
|
(5‑41) |
|
|
(5‑42) |
一方、図 5.4に示すとおり、-i (zk+1 - zk) の方向は zk の方向と等しい。
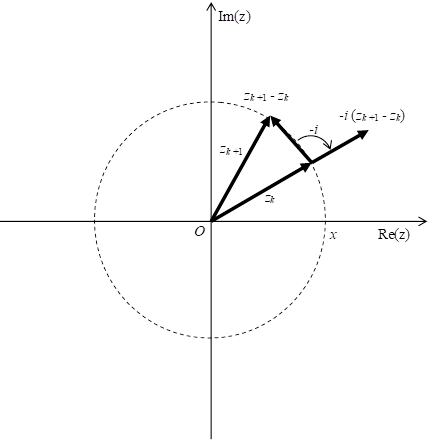
図 5.4:平均アーベル総和法
したがって、1/n は次のように表現できる。
|
|
(5‑43) |
|
|
(5‑44) |
したがって、関数 H (x) は次のように表現できる。
|
|
(5‑45) |
上記の和を次の積分で表現する。
|
|
(5‑46) |
|
|
(5‑47) |
留数定理を適用すると、次の結果が得られる。
|
|
(5‑48) |
したがって、次の新しい一般的な総和法を得る。
(平均アーベル総和法)
|
|
(5‑49) |
|
|
(5‑50) |
|
|
(5‑51) |
|
|
(5‑52) |
この総和法は留数定理により任意の級数を総和できる。
5.4 ε - δ論法による命題の定義
次に示すように、極限値は極限の順序に依存する。
|
|
(5‑53) |
|
|
(5‑54) |
本論文では、極限の順序を次のように定義した。
|
|
(5‑55) |
|
|
(5‑56) |
この極限の順序は次の関係を意味する。
|
|
(5‑57) |
上記の関係をε - δ論法で確認する。
本節では、ε - δ論法で命題を定義する。
関数 Sn と Hn (x) 、定数 α を次のように定義する。
|
|
(5‑58) |
|
|
(5‑59) |
|
|
(5‑60) |
次の命題が成立する。
|
|
(5‑61) |
上記の命題は R - N 論法で次のように表現できる。
任意の正の実数 R に対し、ある適当な自然数 N が存在して、
|
|
(5‑62) |
を満たす全ての自然数 n に対し、
|
|
(5‑63) |
が成り立つ。
次の命題が成立する。
命題 1.
|
|
(5‑64) |
上記の命題はε - δ論法で次のように表現できる。
任意の正の実数ε と、任意の自然数 n に対し、ある適当な正の実数 δ が存在して、
|
|
(5‑65) |
を満たす全ての正の実数x に対し、
|
|
(5‑66) |
が成り立つ。上記の定義は次のようにまとめられる。
|
|
(5‑67) |
次の命題が成立する。
命題 2.
|
|
(5‑68) |
|
|
(5‑69) |
上記の命題はε - δ論法で次のように表現できる。
任意の正の実数ε に対し、ある適当な自然数 N と、ある適当な正の実数 δ が存在し、
|
|
(5‑70) |
を満たす全ての自然数 n に対し、
|
|
(5‑71) |
が成り立つ。
上記の定義は次のようにまとめられる。
|
|
(5‑72) |
次の図において、命題1が 1+2+3+…+nの範囲であり、
命題2が-1/12の範囲である。
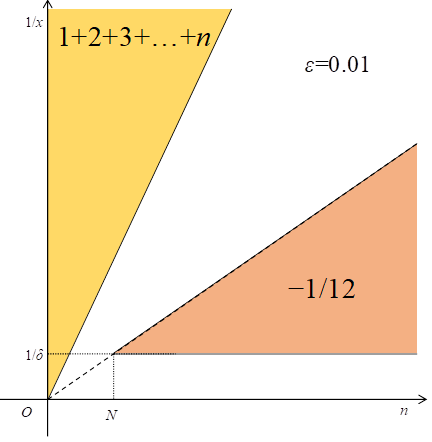
図 5.5: ε - δ論法
6 付録
6.1 自然数のべき乗和の公式の証明
著者は2014年3月に次の公式を発見し、証明した。
(自然数和の公式)
|
|
(6‑1) |
NS氏は2015年3月に上記の式を一般化した次の公式を発見し、発表した。
(自然数のべき乗和の公式)
|
|
(6‑2) |
本節は上記の公式を次の条件で証明する。
|
|
(6‑3) |
6.1.1 コーシーの平均公式
関数F(x)を微分し新しい関数F(1)(x)を得るとき、関数F(x)を母関数、新しい関数F(1)(x)を導関数と呼ぶ。
関数F(q)の変数qに関するs階導関数を次のように表現する。
|
|
(6‑4) |
一方、コーシーの積分公式は次の通り。
(コーシーの積分公式)
|
|
(6‑5) |
|
|
(6‑6) |
コーシーの積分公式の関数F(z)は正則である。もし関数F(z)が正則でないならば、留数定理によって、積分後の関数は元の関数と異なる。関数F(z)が正則でない場合の公式をコーシーの積分公式と区別し、本論文はコーシーの平均公式と呼ぶこととする。
(コーシーの平均公式)
|
|
(6‑7) |
ここで周回経路γは-∞から出発して-∞に帰る反時計回りの経路で、内部にqを含む。
|
|
(6‑8) |
関数f(q)は関数F(z)の周回積分経路上の値の平均値と解釈できる。したがって、コーシーの平均公式は、平均値の定理と解釈できる。本論文では、関数f(q)を平均関数と呼ぶ。平均関数は元の関数と一般的に異なるため、元の関数名F(z)と異なる関数名f(q)を使用する。
コーシーの微分公式は次の通り。
(コーシーの微分公式)
|
|
(6‑9) |
|
|
(6‑10) |
コーシーの微分公式の関数F(z)は正則である。関数F(z)が正則でない場合の公式をコーシーの微分公式と区別し、本論文はコーシーの平均微分公式と呼ぶこととする。
(コーシーの平均微分公式)
|
|
(6‑11) |
ここで周回経路γは-∞から出発して-∞に帰る反時計回りの経路で、内部にqを含む。
|
|
(6‑12) |
関数f (s)(q)を平均導関数と呼ぶ。コーシーの平均微分公式は、関数の平均値を計算し微分するための公式と解釈できる。平均導関数は、母関数の平均のs階導関数と解釈できる。
コーシーの平均公式により導関数で平均導関数を表現できる。
(平均導関数)
|
|
(6‑13) |
ここで周回経路γは-∞から出発して-∞に帰る反時計回りの経路で、内部にqを含む。
|
|
(6‑14) |
ローラン展開により平均導関数で母関数を表現できる。
(母関数)
|
|
(6‑15) |
母関数と平均導関数の関係は次の通り。

図 6.1: 母関数と平均導関数
上記の図は次のように表現できる。
|
|
(6‑16) |
6.1.2 ローラン展開と零位の極
通常、極の位数は次の正の整数nである。
(n位の極)
|
|
(6‑17) |
|
|
(6‑18) |
通常、極の位数は1以上だが、本論文は有限の微小な正の実数hで、次の零位の極(0位の極)を導入する。
(零位の極)
|
|
(6‑19) |
|
|
(6‑20) |
零位の極はz=0で発散している。上記の極のzでの微分は次の通り。
|
|
(6‑21) |
一方、対数の微分は次の通り。
|
|
(6‑22) |
したがって、対数は零位の極と解釈できる。
定数項Cは、次のように、対数関数の引数の係数Bから導出できる。
|
|
(6‑23) |
したがって、零位の項を零位の極とみなす新しい解釈は、零位の項を定数とみなす従来の解釈と矛盾しない。
関数は、対数を含む新しいローラン展開で一意に展開できる。
(対数を含むローラン展開)
|
|
(6‑24) |
|
|
(6‑25) |
ここで周回経路γは-∞から出発して-∞に帰る反時計回りの経路で、内部にOを含む。
|
|
(6‑26) |
関数F(z)が高々零位の極を持つならば、定数AとCで次のように展開できる。
|
|
(6‑27) |
6.1.3 平均調和導関数と平滑自然関数の導入
調和数は次の通り。
(調和数)
|
|
(6‑28) |
調和母関数を次のように定義する。
(調和母関数)
|
|
(6‑29) |
調和母関数の記号としてギリシャ文字η (イータ)の大文字Η (イータ)を使用する。
変数qに関して調和母関数のs階導関数を計算し、調和導関数を得る。
(調和導関数)
|
|
(6‑30) |
調和母関数をコーシーの平均公式で平均化し、平均調和母関数を定義する。
(平均調和母関数)
|
|
(6‑31) |
ここで周回経路γは-∞から出発して-∞に帰る反時計回りの経路で、内部にqを含む。
|
|
(6‑32) |
調和導関数をコーシーの平均公式で平均化し、平均調和導関数を定義する。
(平均調和導関数)
|
|
(6‑33) |
ここで周回経路γは-∞から出発して-∞に帰る反時計回りの経路で、内部にqを含む。
|
|
(6‑34) |
コーシーの平均微分公式を調和母関数に適用し、平均調和導関数を得ることができる。
(平均調和導関数)
|
|
(6‑35) |
ここで周回経路γは-∞から出発して-∞に帰る反時計回りの経路で、内部にqを含む。
|
|
(6‑36) |
調和母関数と平均調和導関数の関係は次の通り。
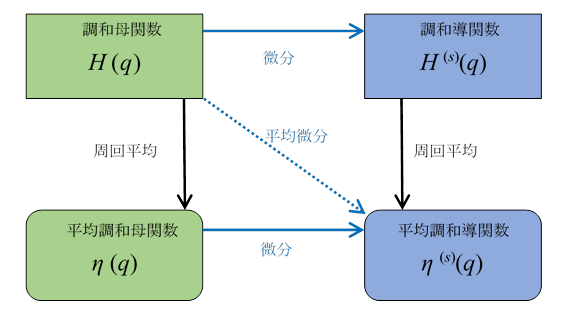
図 6.2:調和母関数と平均調和導関数の関係
上記の図は次のように書ける。
|
|
(6‑37) |
自然数は次の通り。
(自然数)
|
|
(6‑38) |
自然関数を次のように定義する。
(自然関数)
|
|
(6‑39) |
自然関数の記号としてギリシャ文字ν (ニュー)の大文字Ν (ニュー)を使用する。
自然関数を量子化し波動自然関数を得る。
(波動自然関数)
|
|
(6‑40) |
波動自然関数をコーシーの平均公式で平均化し、平均波動自然関数を定義する。
(平均波動自然関数)
|
|
(6‑41) |
ここで周回経路γは-∞から出発して-∞に帰る反時計回りの経路で、内部にqを含む。
|
|
(6‑42) |
平滑自然関数を上記の平均波動自然関数の古典極限で定義する。
(平滑自然関数)
|
|
(6‑43) |
上記のように、関数を量子化し、周回平均値を計算し、古典極限を取る操作を本論文では平滑化と呼ぶこととする。
次の図のように自然関数を平滑化し、平滑自然関数を得ることができます。
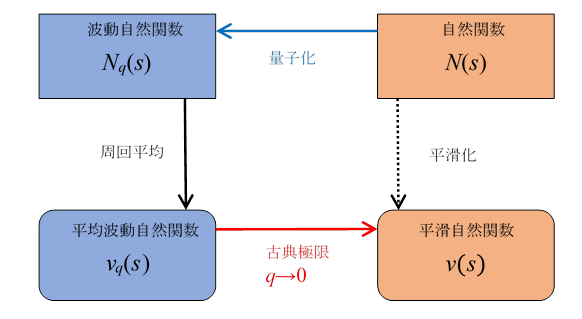
図 6.3: 自然関数を平滑化し平滑自然関数を得る。
上記の図は次のように表現できる。
|
|
(6‑44) |
本節の関数の関係は次の通り。
|
|
(6‑45) |
6.1.4 解析接続の意味
解析接続の意味は何だろうか?本節ではその意味を考察する。
リーマンは次のゼータ関数を定義した。
(ゼータ関数)
|
|
(6‑46) |
そしてリーマンは1859年にゼータ関数の解析接続を次の周回積分で定義した。
(ゼータ関数の解析接続)
|
|
(6‑47) |
ここで周回経路γは-∞から出発して-∞に帰る反時計回りの経路で、内部にOを含む。
|
|
(6‑48) |
数学者ワイエルシュトラスは、1842年に解析関数の解析接続を単性解析関数と呼んだ。一方、数学者アールフォルスは1979年に大域的解析関数と呼んだ。大域的解析関数という名称がリーマンの考えに近いと推測するため、本論文ではゼータ関数の解析接続を大域ゼータ関数と呼ぶ。
大域ゼータ関数は元のゼータ関数と異なる。そこで元のゼータ関数と大域ゼータ関数を区別するため、元のゼータ関数の記号としてギリシャ文字ζ (ゼータ)の大文字Ζ (ゼータ)を使用する。
(ゼータ関数)
|
|
(6‑49) |
上記の和の各項にexp(nq)をかけ、次の波動ゼータ関数を定義する。
(波動ゼータ関数)
|
|
(6‑50) |
上記の変換を量子化と呼ぶ。
波動ゼータ関数を平均化し平均波動ゼータ関数を得る。
(平均波動ゼータ関数)
|
|
(6‑51) |
ここで周回経路γは-∞から出発して-∞に帰る反時計回りの経路で、内部にqを含む。
|
|
(6‑52) |
平均波動ゼータ関数の古典極限を取り、大域ゼータ関数を得る。
|
|
(6‑53) |
解析接続は、関数を量子化し、その周回平均値を取り古典極限を取る操作を意味する。
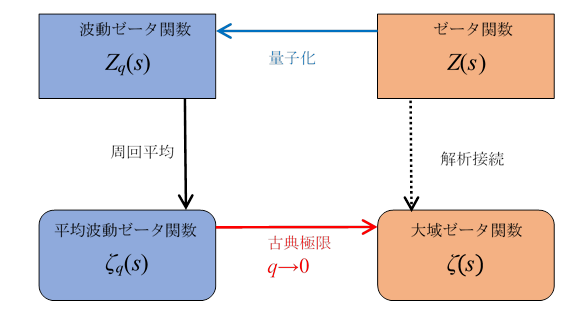
図 6.4: 大域ゼータ関数
上記の図は次のように書ける。
|
|
(6‑54) |
本節の関数の関係は次の通り。
|
|
(6‑55) |
平滑自然関数と大域ゼータ関数は次の関係を持つ。
|
|
(6‑56) |
したがって、平滑化は解析接続と同じ操作である。
6.1.5 調和導関数による自然数和の公式の証明
次の条件を設定する。
|
|
(6‑57) |
調和母関数は次の通り。
(調和母関数)
|
|
(6‑58) |
上記の関数は次のように変形できる。
|
|
(6‑59) |
ランダウの記号を使い、調和母関数の極の位数を次のように計算する。
|
|
(6‑60) |
調和母関数は q = 0 で零位の極を持つため、定数A, C を使い q = 0 で次のようにローラン展開できる。
(調和母関数のローラン展開)
|
|
(6‑61) |
上記の式の二階導関数を計算する。
|
|
(6‑62) |
自然数和の公式は次のように証明できる。
|
|
(6‑63) |
|
|
(6‑64) |
|
|
(6‑65) |
|
|
(6‑66) |
(証終)
調和母関数の実際のローラン展開は次の通り。
|
|
(6‑67) |
したがって、次のことがわかる。
|
|
(6‑68) |
|
|
(6‑69) |
|
|
(6‑70) |
|
|
(6‑71) |
|
|
(6‑72) |
|
|
(6‑73) |
|
|
(6‑74) |
6.1.6 平均調和倍音導関数と平滑自然倍音関数の導入
調和倍音母関数を次のように定義する。
(調和倍音母関数)
|
|
(6‑75) |
変数qに関して調和倍音母関数のs階導関数を計算し、調和倍音導関数を得る。
(調和倍音導関数)
|
|
(6‑76) |
調和倍音導関数をコーシーの平均公式で平均化し平均調和倍音導関数を定義する。
(平均調和倍音導関数)
|
|
(6‑77) |
上記の関数の関係は次の通り。
|
|
(6‑78) |
ここで周回経路γは-∞から出発して-∞に帰る反時計回りの経路で、内部にqを含む。
|
|
(6‑79) |
平均調和倍音導関数の古典極限で平滑自然倍音関数を定義する。
(平滑自然倍音関数)
|
|
(6‑80) |
コーシーの平均微分公式を調和倍音母関数に適用し、平滑自然倍音関数を得ることができる。
(平滑自然倍音関数)
|
|
(6‑81) |
ここで周回経路γは-∞から出発して-∞に帰る反時計回りの経路で、内部にOを含む。
|
|
(6‑82) |
本節の関数の関係は次の通り。
|
|
(6‑83) |
平滑自然関数とゼータ関数の解析接続の関係は次の通り。
|
|
(6‑84) |
6.1.7 平均調和倍音導関数による自然数のべき乗和の公式の証明
次の条件を設定する。
|
|
(6‑85) |
すると、1以上のkについて次の式が成り立つ。
|
|
(6‑86) |
さらに、次の条件を設定する。
|
|
(6‑87) |
すると、1以上のkについて次の式が成立する。
|
|
(6‑88) |
したがって、qの絶対値を十分小さく選べば、次の式が成立する。
|
|
(6‑89) |
上記の結果より、調和倍音母関数の絶対値は、調和母関数よりも小さいため、調和倍音母関数は調和母関数よりも高位の極を持たないことがわかる。
ランダウの記号を使い、q=0における調和母関数の極の位数を次のように計算する。
|
|
(6‑90) |
調和母関数はq=0で零位の極を持つ。そのため、調和倍音母関数はq=0で高々零位の極を持つ。そこでtに依存する関数A(t)と関数 C (t) を用い、調和倍音母関数をq=0で次のようにローラン展開する。
(調和倍音母関数のローラン展開)
|
|
(6‑91) |
上記の式の二階導関数を計算する。
|
|
(6‑92) |
自然数のべき乗和の公式は次のように証明できる。
|
|
(6‑93) |
|
|
(6‑94) |
|
|
(6‑95) |
|
|
(6‑96) |
(証終)
6.1.8 第二証明
前節では、自然数のべき乗和の公式を次の条件で証明した。
|
|
(6‑97) |
本節では、次の条件でその公式を証明する。
|
|
(6‑98) |
上記の条件では、自然数kについて次の式が成り立つ。
|
|
(6‑99) |
ゆえに、次の式が成り立つ。
|
|
(6‑100) |
さらに、次の条件を設定する。
|
|
(6‑101) |
すると、自然数kと、十分小さいzに対し次の式が成立する。
|
|
(6‑102) |
同様に、自然数kと、十分小さいzに対し次の式が成立する。
|
|
(6‑103) |
したがって、次の関数の絶対値は単調減少する
|
|
(6‑104) |
次の図に示す通り、初項ezと、1から無限大までの関数f(x)の積分は調和倍音母関数より大きい。

図 6.5: 調和倍音母関数
ゆえに、十分小さいzに対し次の不等式が成立する。
|
|
(6‑105) |
ここで次のように変数変換する。
|
|
(6‑106) |
両辺を微分する。
|
|
(6‑107) |
|
|
(6‑108) |
|
|
(6‑109) |
|
|
(6‑110) |
したがって、積分は次のように変数変換できる。
|
|
(6‑111) |
ここで次の関数を考える。
|
|
(6‑112) |
次の図の通り、調和母関数は、1から無限大までの関数g(y)の積分より大きい。
図 6.6: 調和母関数
そのため、十分小さいzに対し次の不等式が成立する。
|
|
(6‑113) |
前節の通り、下記式の右辺は、z=0で零位の極を持つ。
|
|
(6‑114) |
したがって、前節の通り、次の式が成立する。
|
|
(6‑115) |
(証終)
6.2 ヤコビのテータ関数
リーマンは、ヤコビのテータ関数でゼータ関数を表現した。
(ヤコビのテータ関数によるゼータ関数の表現)
|
|
(6‑116) |
|
|
(6‑117) |
(ヤコビのテータ関数)
|
|
(6‑118) |
|
|
(6‑119) |
ヤコビのテータ関数と調和倍音母関数の関係は次の通り。
|
|
(6.120) |
(調和倍音母関数)
|
|
(6‑121) |
コーシーの平均公式により次の平均調和倍音導関数を得る。
(平均調和倍音導関数)
|
|
(6‑122) |
ここで周回経路γは-∞から出発して-∞に帰る反時計回りの経路で、内部にOを含む。
|
|
(6‑123) |
また、コーシーの平均微分公式でも上記の関数を得ることができる。
|
|
(6‑124) |
ここで周回経路γは-∞から出発して-∞に帰る反時計回りの経路で、内部にOを含む。
|
|
(6‑125) |
調和倍音母関数でゼータ関数を表現できる。
(調和倍音母関数によるゼータ関数の表現)
|
|
(6‑126) |
ここで周回経路γは-∞から出発して-∞に帰る反時計回りの経路で、内部にOを含む。
|
|
(6‑127) |
(調和倍音母関数)
|
|
(6‑128) |
6.3 ゼータ関数のq類似
ジャクソンは1904年に次の量子化された新しい自然 数、q数を定義した[8]。
(q数)
|
|
(6‑129) |
|
|
(6‑130) |
|
|
(6‑131) |
量子化した数学的対象を一般にq類似と呼ぶ。自然数nのq類似がq数 [n]q である。q数の古典極限で自然数を表現する。
|
|
(6‑132) |
ゼータ関数は次のとおり。
(ゼータ関数)
|
|
(6‑133) |
ゼータ関数のq類似はqゼータ関数である。その関数は次のとおり7。
(qゼータ関数)
|
|
(6‑134) |
ゼータ関数はqゼータ関数の古典極限で表現できる。
|
|
(6‑135) |
|
|
(6‑136) |
|
|
(6‑137) |
|
|
(6‑138) |
q数と有限調和導関数の関係は次の通り。
|
|
(6‑139) |
|
|
(6‑140) |
6.4 ゼータ関数と分配関数、調和数の関係
次の有限調和導関数を定義する。
(有限調和導関数)
|
|
(6‑141) |
調和数は有限調和導関数の極限で表現できる。
|
|
(6‑142) |
分配関数を次のように定義する。
(分配関数)
|
|
(6‑143) |
有限調和導関数の極限で分配関数を表現できる。
|
|
(6‑144) |
リーマンはゼータ関数を定義した。
(ゼータ関数)
|
|
(6‑145) |
|
|
(6‑146) |
ゼータ関数は有限調和導関数の極限で表現できる。
|
|
(6‑147) |
以上の結果は次のようにまとめられる。
- 調和数は、有限調和導関数の極限である。
- 分配関数は、有限調和導関数の極限である。
-ゼータ関数は、有限調和導関数の極限である。
それらの関係を次の図に示す。
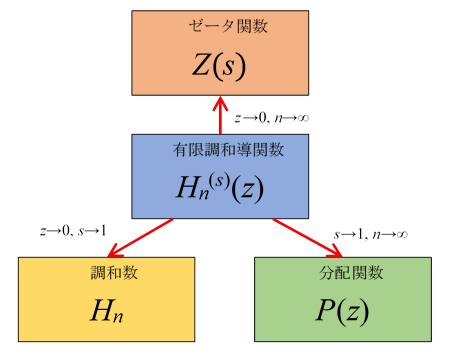
図 6.7: ゼータ関数
上記の図は次のように書ける。
|
|
(6‑148) |
7 謝辞
本論文を作成するにあたり、貴重な助言を頂いたNS氏に心より感謝いたします。
8 参考文献